海洋内波发展演变数值试验

邓 冰,张宇飞,张 铭

(1.北京应用气象研究所,北京100029; 2.中国海洋大学海洋与大气学院,山东青岛266100; 3.解放军理工大学气象海洋学院,江苏南京211101)

海洋内波发展演变数值试验

邓 冰1,张宇飞2,张 铭3

(1.北京应用气象研究所,北京100029; 2.中国海洋大学海洋与大气学院,山东青岛266100; 3.解放军理工大学气象海洋学院,江苏南京211101)

利用二维非静力数值模式,对海洋跃层中剪切背景流下内波做了线性和非线性模式的数值试验,结果表明:在本文所取的初始场和环境参数下,海洋内波密度扰动大值中心始终出现在密度跃层附近,被跃层所俘获,这与实际观测相一致;线性情况下,流函数扰动中心与密度扰动中心有很好地配合,密度扰动正、负中心附近分别存在流函数扰动的正、负单圈环流中心,且单圈环流垂直贯穿整个水体。线性模式中内波扰动强度在调整适应期后一直呈指数增长发展,剪切背景流是不稳定的;而非线性情况则呈准线性增长发展,以后增长停止而进入稳定期,且后者的增长也比前者要慢;非线性效应抑制了内波增长而使之趋于稳定,具有维稳作用。随着积分时间增加,线性模型中内波波包波形基本不变。波包的负、正振幅大体相同,整个波包宽度也基本不变,仅振幅有所增长;内波波包传播速度与其振幅无关,且传播速度基本不变。非线性情况下内波波包的形状则发生改变,其负、正振幅之比越来越大,波峰前的陡降也越来越强;并且内波传播速度与其振幅和波形有关,通常非线性效应越强,内波传播越慢。从本文中海洋内波的波长、周期和传播速度来看,该内波属于高频内波(短周期内波),性质为内重力惯性波。

数值试验;海洋内波;跃层;剪切背景流

海洋内波是发生在海水密度稳定层化海洋中的波动,它在海洋中普遍存在,无论在大洋中部还是在近岸、大陆架或大陆坡都观测到过内波。偏离平衡位置的水质点受到恢复力的作用,则会出现内波[1]。海洋内波不仅对海洋的物理特性有重要影响,而且对人类的海洋活动,特别是军事活动有很大的影响[1]。海洋内波的生成机制一直是一个倍受关注的研究课题。有很多因素都能激发内波,它们可来自海面、海底和海水内部。目前,普遍认为,在陆架区,潮汐和地形相互作用是内波的主要生成机制,表面潮通过剧烈变化的地形(如陆架坡折处、海峡、海岭和海沟等)而生成内波,且是地形处等密度面受表面潮强迫的响应[2]。潮汐与地形相互作用概括了潮成内波的生成机制,可满意解释发生于陆架陆坡临近海域及浅海中的内潮波。然而,在明显不存在潮汐与地形相互作用的条件下,观测到海洋内波也常被报道[3-5]。当前关于不同内波生成机制的研究也在逐步深入,例如,河口羽流[6]、海底地形特征的波动、黑潮流场的不稳定性以及温跃层变浅等因素都可激发内波。Mack等[7]分析了从140°～110°W的热敏电阻测温观测资料之后,认为剪切背景流的不稳定是赤道东太平洋上层内波失稳和湍流混合的主要机制。袁业立等[8-9]通过分析南中国海北部的内波SAR图像,并且应用内波线性理论,探讨了该海域内波的生成机制;他们基于海洋内波的控制方程建立了一个线性波理论模型,用来分析黑潮的不稳定性;他们指出,对于向西传播的扰动,黑潮西翼流场是不稳定的,此情况下内波从黑潮吸收能量并且增长,其传播方向向西;并提出了黑潮流场的不稳定性可以激发内波的新观点;此外他们还利用上述模型解释了卫星SAR图像观测到的内波与黑潮西边界的共存现象,从而进一步验证了黑潮流场的不稳定性确实可激发内波的观点。在某些特殊的情况下,水中潜艇的螺旋桨推进器对稳定层化海水的扰动也能诱发相应的高频随机内波。与潜艇诱发海洋内波类似,海洋内部其他局部动力或运动扰动源也可以在层化海洋中激发内波[10]。Zheng等[11]结合SAR图像和实测资料对南中国海北部发现的内波进行了统计和动力分析,并在此基础上提出,温跃层变浅为向西传播初始扰动的振幅增长提供了外部驱动;由于向东传播的初始扰动没有机会增长,因而在吕宋海峡东部几乎观测不到内波。Li和Farmwr[12]对中国南海西北部孤立波的生成和演变做了数值研究,揭示了地形对内波生成的影响,并指出在地形附近存在不同模态的内波,第一和第二模态内波可以传播到较远的地方。Li和Farmwr[13]则研究了中国南海深海盆中非线性内波的产生和演变。

(王 燕 编辑)

在海洋中,各种波动常常在某些条件下产生并得到发展,而在另一些条件下受到抑制和阻尼。初始扰动的存在和内波振幅的增长是内波产生的充分必要条件;初始扰动可通过潮汐、潮汐与地形的相互作用、以及西边界流的不稳定性等来实现,然而初始扰动的存在仅是内波产生的必要条件而非充分条件。由于扰动能量的耗散,只有充分增长的波动才可能从源区辐射开来,故内波的存在应与其不稳定密切有关。利用标准模方法,将波动稳定性问题转化为其本征值的边值问题,是求解其稳定性问题常用的有效方法[14],然而其仅能解决线性稳定性问题,对非线性稳定性问题失效,此时必须用另外的方法来研究[15]。采用数值试验方法则能研究波动的发展演变问题,其中也包括波动的线性和非线性不稳定问题,且早已应用于研究同样是地球流体的大气中的波动[16];为此对于海洋内波的发展演变问题,同样可采用数值试验方法来研究,当然在此必须考虑海洋自身的特点。

本文将内波发展演变问题看作一个初值问题,采用一个二维非静力的Boussinesq方程组[17]来描写,并依据该方程组设计了一个数值模式[18],用数值试验的方法来研究在海洋跃层和剪切背景流下海洋内波的发展演变问题,揭示在该情况下线性和非线性海洋内波的发展演变规律,同时给出该海洋内波的扰动结构和振荡周期。

1 数值模式和实验方案

本文采用邓冰等[17]所用的二维非静力Boussinesq方程组,考虑了海洋跃层的存在和背景流的作用,但不考虑海底地形。设水平背景流的流向为x方向,扰动(内波)则也沿着该方向传播。扰动等位相面的水平方向为y方向,设在y方向扰动是均匀的,即对扰动量的y方向求导为0。z方向则由海底垂直指向海面,并设海底z=0。这样该数值模式的控制方程组为[18]

模式水平方向取401个格点,格距为100 m,水平范围为40 km,垂直范围取1.2 km,分为24层,层距为50 m。水平侧边界取海绵边界条件。空间差分取中央差,时间积分取前差叠代方案,积分时间步长取为6 s。模式中考虑到在水深250 m处有跃层存在,其位于模式的第19层上,在该处取层结参数N2=10-4/s2,而其之上、下则均取N2=10-8/s2。这样取是考虑到实际海洋中除跃层外密度垂直变化都很小的缘故。模式的背景流:在海底至距海底350 m处为0,之上至海表呈线性变化,海表值取为1.5 m/s。模式中取地转参数f为常数,其值为10-4/s2。

模式初始场设流场为0,位密度场为一个垂直和水平方向均为半个波长的简谐波,垂直方向半波长为600 m,即为海洋水深的一半,水平半波长为400 m,占5个格点,其中心值(振幅)为10-3m/s2,水平方向该值位于第40个格点处,如图1所示;该图中已将位密度扰动σ'通过公式ρ'= -ρ0σ'/g转换成密度扰动ρ',下文中均将位密度转换为密度并绘图。图1中横坐标方向为x方向,其标注为水平距离,纵坐标方向为z方向,其标注为水深,本文以下空间分布图的坐标和标注均与此相同;此外,模式中用流函数来表示流场扰动,在其正、负中心的外围分别有顺、逆时针旋转的环流圈,而其等值线的密疏则反映扰动速度的大小,这些以下都不再赘述。本文数值试验中模式积分的时间为36 h。通过实践,表明该数值模式积分是稳定的,可积分72 h以上。

图1 初始扰动密度场分布Fig.1 Distribution of initial density disturbance

2 线性模式内波发展演变分析

利用上述的线性化控制方程组来做此数值试验,可分析剪切背景流的失稳和内波的发展过程。这里的背景流和层结参数以及初始条件均取上面的方案。

2.1 内波流函数和密度场分布

在计算区域中本文取沿背景流方向的扰动速度最大值u'max随时间的变化来反映波动增长的大小,并用此分析波动的发展情况。由于本文给出的初始场只有位密度场而无流场,故在开始积分之后,流场和位密度场会相互调整,以便彼此适应。

图2给出了u'max随时间增长图。图中横坐标为积分小时,纵坐标为u'max值,由该图可见,在积分3 h后可认为此调整已大体完成;以后u'max随时间呈指数增长,到18 h后u'max值已达2 m/s以上。之后,这种指数增长的状态一直持续至积分终了。由此可见,在线性情况下,该剪切背景流是不稳定的,内波呈指数增长的发展态势。

图2 线性模式中u'max值随时间变化Fig.2 Variation of u'maxin linear model

积分1 h密度扰动和流函数的空间分布见图3a。图中等值线为流函数,填色图为密度扰动。可见,初始时刻原在底层的密度扰动,积分1 h后,主要体现在跃层处,而底层的密度扰动已经很弱,流函数的大值区仍然在底层;此时流场和密度场处于相互调整,彼此适应的阶段。

随着积分时间的增加,密度扰动向右即向x方向传播,强密度扰动仍发生在跃层处,强流函数中心也在跃层处。在积分10 h,在密度扰动正、负中心附近分别有一个正、负的流函数环流圈中心,整个流函数环流圈上下垂直贯穿整个水体(图3b)。

积分20 h密度扰动强度增大,并继续向右传播,而流函数环流中心与密度扰动中心的配置与10 h类似(图3c)。随着密度扰动的发展,流场也在加强,流函数在整个海域一直表现为从海底到海表的单圈环流形式,并沿着背景流向右传播。密度扰动的大值区主要在跃层处,但流函数环流则更向海洋深层伸展。

从积分到30 h的密度扰动和流函数分布情况看(图3d),两者的配置与20 h(图3c)相似,但强度增大了1个量级。此时密度扰动中心仍然集中在跃层处,流函数环流圈也上下贯穿整个水体。积分到30 h后,密度扰动和流函数环流圈均移近右边界,再往后则移出了右边界。

图3 线性模型中密度扰动和流函数的空间分布图Fig.3 Distribution of density disturbance and stream function in linear model

2.2 内波周期和波长

在跃层处密度扰动的变化情况,能很好地反映海洋内波的发展演变情况,并能确定该内波的周期、频率、波长和振幅。

图4a为跃层(第19层,水深250 m,下同)处在水平格点150上的密度扰动随积分时间的变化,由该图可见,其大体呈单峰两谷形态;在积分9 h,密度扰动有微弱增强,以后则减小,2 h后达到第一个波谷,也是最低的波谷,其值约为-0.4 kg/m3。再经3 h至积分14 h,密度扰动达到最高峰(最大值),峰值为0.83 kg/m3,后再积分至16 h,密度扰动达到第二个低谷,其值为-0.42 kg/m3。由密度扰动随时间的变化可知,其振荡周期约为5 h,相应的振荡频率为0.34×10-3/s。

该跃层处其他水平格点上的密度扰动随时间变化也有类似规律,参见图4b;此图为格点200上密度扰动随时间的变化,其也呈单峰两谷形态,这里在19 h密度扰动达到最大值,为2.5 kg/m3,扰动周期和频率均与图4a中大致相同。在此因达到最大值的时间比图4a中晚了5 h,故密度扰动最大值要比图4a中约大3倍。从以上的周期和频率看,该内波属高频内波。

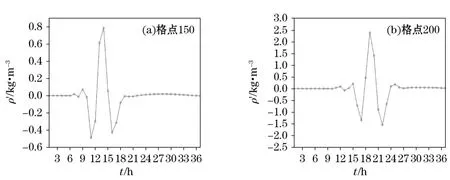
图4 线性模型中跃层处密度扰动随积分时间的变化Fig.4 Variation of density turbulence in linear model

为考察该内波的波动形态及波长,图5分别给出了积分的10,20,30 h,在跃层处密度扰动的水平分布。由图5可见,在积分10 h,密度扰动分布大体呈3峰3谷的波包形态。此波包中左方波动的强度明显要大于右方,波长也较右方的要长。该左、右方波动的波长分别约为4.8和3.8 km。随着积分时间增加,此密度扰动波包形态大致不变,仍呈3峰3谷形态,波包中该左方波动仍为最明显的波动,该左、右两方波动的波长变化也不大。此波包沿着背景流传播。在积分10,20,30 h,此波包强度的最大值即该左方波动的峰值分别为0.55,3.5,24 kg/m3。积分30 h该峰值要比积分10 h增加了43倍,这是因失稳的剪切背景流下波动振幅呈指数增长的缘故。在积分30 h以后,此波包移出了右边界。

因在时间积分中此波包形态变化不大,故可推测此波包中的波动应有大致相同的相速c,该相速可从此波包在一定时间内其向右移动的距离来估算。结果是该相速约为0.28 m/s。由该相速c,依据相应的波长L,则也能估算其振荡频率为2πc/L及周期为L/c。由此估算的振荡频率为0.37×10-3s-1,周期为4.8 h。将这里估算的周期4.8 h与以上根据密度扰动随时间变化所得到的周期5 h相比,两者很接近。由以上的波长和周期看,此波包中的波动均为短周期内波,即短波长的高频快波。

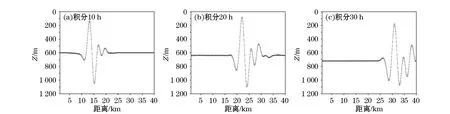
图5 线性模型中跃层处密度扰动的水平分布Fig.5 Distribution of density disturbance with distance in linear model

3 非线性模式内波发展演变分析

本节分析非线性模式内波的发展和演变规律,模式中的环境条件(背景流和层结参数)以及初始场与线性模式的取值相同。

3.1 内波的发展演变

用沿背景流方向的扰动速度最大值随时间的变化来反映波动的发展演变,图6给出了该最大值随时间的变化情况。由图6可见,扰动在开始的3 h内变化激烈,这同样反映了上述速度场和位密度场之间相互调整彼此适应的过程,以后该最大值以准线性的形式稳步增长,到23 h,该值达到0.4 m/s左右;之后该值在0.4 m/s附近摆动,无明显增长趋势,这表明扰动已基本稳定。将图6与图2相较可见,在非线性情况下,在内波积分23 h前的发展期,其增长要较线性情况慢,且呈准线性增长,而不像线性情况下的指数增长;在积分23 h后,则基本停止增长而保持稳定,由此可见非线性效应对其有维稳作用。

图6 非线性模式中u'max值随时间变化Fig.6 Variation of u'maxin nonlinear model

从密度扰动的分布看(图7a),1 h后,大的密度扰动区与线性情况(图3a)类似,也发生在密度跃层处,而流函数的大值区则仍在海洋下层。随着积分时间的增加,扰动沿着背景流向右移动,密度扰动在加强。

图7 非线性模式密度扰动和流函数的空间分布图Fig.7 Distribution of density disturbance and stream function in nolinear model

积分10 h(图7b),密度扰动的强中心仍出现在跃层处,与线性情况相比(图3b),密度扰动正、负中心的距离拉大,即扰动波长增大,扰动所占的范围也要大;从流函数分布看,在密度扰动正、负中心的附近均有流函数的正、负环流圈与之相配合,且这些环流圈也大体上下垂直贯穿整个水体,这与线性情况相类似(图3b)。积分20 h,扰动仍向右移动,跃层处的密度扰动中心进一步增强,达到鼎盛期(图7c);此时密度扰动水平分布范围更广,最长的扰动水平波长也更长;而流函数则仍以单圈环流为主;在密度扰动的正、负中心附近,也均有正、负流函数环流圈与之对应,但此时密度扰动中心与流函数环流中心已不完全重合,流函数环流圈中心多在跃层略偏下的部位,且负环流的强度要明显大于正环流,这与线性情况已有所不同,那里两者强度的差别没有这样大(图3c)。积分30 h,密度扰动继续沿着背景流右移,密度扰动的强中心仍在跃层处,密度扰动和流函数中心的强度与20 h相差不大,但两者配置较那时已有所改变;虽然此时仍具有流函数负环流圈的中心均在跃层略偏下的部位,且负环流的强度要明显大于正环流的特点,但是流函数正环流圈的中心则多位于海洋中下层,此外扰动的最长波长要较积分20 h的略有减小。

3.2 跃层处密度扰动的时空变化

在非线性模式中,密度扰动的大值中心与线性情况类似,也均出现在跃层处,在此分析密度扰动在该处的时空变化,并与线性情况作对比分析。

图8a为跃层处水平格点为150处密度扰动随积分时间的变化,可见,在7 h前因波动还未传播到该点,故无密度扰动,这与线性情况相同,以后随着波动的传到,密度扰动出现了波动,在该格点上第一、二、三个波动分别出现在积分7～13.5,13.5～22.5,22.5～36 h,其周期分别约为6.5,9,13.5 h,且后一个波动的周期都较前一个的要长,与线性情况相比,这里的周期也都比那里的要长;据此可知,非线性作用越强,波动周期则越长。非线性情况与线性情况另一个不同是,前者波动要完全移过该点所需的时间远较后者要长,前者至积分终了时(积分36 h)波动才大体移过该点,而后者在19 h波动就已移过该点了(图4a)。从图8a上波动的波形看,第一个波动与简谐波虽尚有相似之处,但波形已开始出现不对称,第二、三个波动这种不对称更明显,特别是第三个波动,其负振幅要远远超过正振幅,且波形也与简谐波差异更大。这表明,随着积分时间增加,非线性效应在不断加大,初始的简谐波动演变为非线性波动。以上所列举的非线性波动的特征,这与图4a中的线性波包有明显差别。

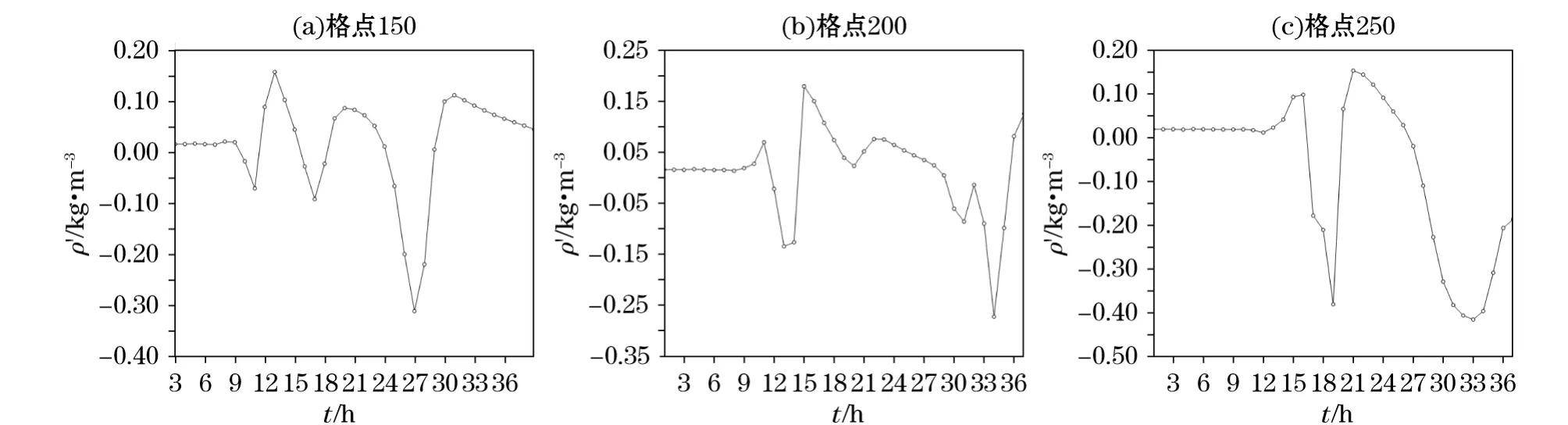
图8 非线性模式中跃层上密度扰动随积分时间的变化Fig.8 Variation of density disturbance in nonlinear model

图8b为水平格点200处的密度扰动随积分时间的变化,该格点处于图8a中格点的右方,波动传播到该点需10 h,以后该点出现非线性波动直至积分终了。由于该格点值为200,要比图8a中的值150大,该格点处非线性效应则更强;此时第一个波动的周期为8.5 h(从积分11.5至20 h),与图8a中相比,周期也更长;在积分14至15 h波动就有明显陡升,从波形看,这里的情况与相应线性的情况(图4b)差异更大。

图8c为水平格点250处的密度扰动随积分时间的变化,此时因该格点值更加大,波动要至积分13 h才能抵达,且非线性效应更强。此时第一个波动的周期约为9.7 h(从积分16.3至26 h),周期较图8b中的也更长;该波动的陡升也比图8b中的更大。

波动最前方波阵面传到格点200与格点150的时差为3 h,格点250与格点200的时差为4 h,根据这2个时差以及在该时差中波阵面移过的距离(均为5 km),则可分别估算出该波阵面的传播速度c,其分别为0.46,0.35 m/s。因后者的非线性效应较前者更强,故可知非线性效应越强,该非线性波动的波阵面传播得越慢。用以上2个速度通过图8a,b中分别得到的第一个波动的周期(其为6.5,8.5 h),就可估算图8a,b中第一个波动的波长L(因波长L等于波速c乘该周期),其分别为10.8,10.7 km。

本文进一步分析了跃层处密度扰动的水平分布。图9a给出了积分10 h在该跃层上密度扰动的水平分布。由图可见,此时波阵面已抵达格点240附近,而同时波动已完全移过了格点60,整个波动的宽度占约180格距即18 km。这时波形已与线性情况有明显区别,波动的负振幅要明显大于正振幅,在最高波峰右侧即该峰前有十分剧烈的向下陡降。在整个波动宽度中有十分明显的一个波峰和两个波谷,可认为其包含了1.5个波,故其波长约为12 km,而这与以上估算的图8b中第一个波动的波长10.8 km相近。

图9b为积分20 h密度扰动的水平分布。此时波阵面已抵达并超越了模式的右边界,整个波动则移过了格点90,其范围超过了310个格距即31 km,比图9a中的18 km要大1倍以上。从该图上的波形可见,此时波动的正振幅与负振幅更不对称,波峰前的向下陡降更加猛烈,这是由于此时如上所述非线性效应更强的缘故。图9c给出了积分30 h的分布。此时扰动已移过格点120处,该图中波动的形态与图9b类似,只是因此时非线性效应进一步增强,波峰前的向下陡降比图9b中还要猛烈。

图9 非线性模式中跃层处密度扰动的水平分布Fig.9 Distribution of density disturbance with distance in nonlinear model

4 讨 论

从以上试验结果看,无论是线性还是非线性的情况,当存在跃层时,密度扰动的大值中心始终出现在跃层处。线性情况下流函数与密度扰动中心有很好的配合,后者的正、负值中心附近分别配合有前者的正、负单圈环流,该环流上下贯穿整个水体。非线性情况下,两者的配合则有所改变。张翔等[18]的试验也是这样,尽管未直接给出密度扰动的情况。这表明,有、无跃层两者有很大差别,密度扰动中心为跃层所俘获。在实际中通常也观测到跃层附近密度扰动最显著,本文试验结果很好地体现了该点。

比较本文剪切背景流下线性与非线性模式试验的结果,其两者的主要差别有以下3点:

1)线性情况扰动在调整适应期后其强度一直呈指数增长的发展态势,该剪切背景流是不稳定的;而非线性情况扰动强度先呈准线性增长,此为扰动的发展期,这时该增长明显比线性指数增长要慢,以后扰动强度则不再明显增长而进入稳定期。这表明,非线性效应抑制了扰动的增长,最终使扰动趋于稳定,具有维稳作用;然而由于该数值实验模型所用控制方程组要较穆穆[15]研究中的正压大气复杂,对于该模型控制方程组的非线性稳定性[15],目前尚无理论上的证明。

2)线性情况下波包的波形大体不变,波包的正振幅和负振幅两者大体相同,随着积分时间增加,整个波包的宽度也大体不变,这反映了在线性情况下叠加原理成立,波包中各波动的波长保持不变,且无相互作用;非线性情况下则与之有所不同,波包的形状随积分时间的增加而发生改变,在水平格点上其负振幅与正振幅的比越来越大,其波峰前的陡降也越来越强烈;若这种情形一直继续,会导致波峰前出现间断,这是由于非线性的追赶效应所致。由于非线性情况存在波与波的相互作用,从而使波动出现频移(变频效应),产生更快和更慢的波动,从而使得波包所占的宽度也有明显加大。

3)线性情况下扰动波包的传播速度与其振幅无关,其传播速度大体不变;可通过多种方法来估算其波长、频率和周期,并得到大致相同的结果;非线性情况扰动传播的速度与其振幅和波形有关,非线性效应越强,波动传播得越慢。

从本文数值实验中波动的波长L、周期T和传播速度c来看,其量级分别为10 km,10 h和1 m/s,属于高频内波(短周期内波),此时Rossby数Ro=c/(f·L)=1/(10-4·10×103)=1。由此可见,本文的海洋内波属非平衡内波[14],若时间尺度在6 h之内则可忽略地球自转的效应,其性质则为内重力波;然而本文内波时间尺度已超过6 h,该效应不宜忽略,故本文内波的性质应是内重力惯性波。

5 结 语

本文采用二维非静力Boussinesq控制方程组[17]以及据此研制的数值模式[18],对存在海洋跃层和剪切背景流的海洋内波做了线性和非线性模式的数值试验,并对结果做了分析、比较和讨论,在本文所取的初始场和环境参数下,所得主要结论有:

1)海洋内波密度扰动的大值中心始终出现在跃层处,其为跃层所俘获,这与实际观测相一致;线性情况下流函数与密度扰动中心有很好的配合,密度扰动正、负中心附近分别存在流函数扰动的正、负单圈环流,且单圈环流垂直贯穿整个水体;非线性情况下则有所改变。

2)线性情况内波扰动强度呈指数增长发展,剪切背景流是不稳定的;而非线性情况则内波扰动强度在初期呈准线性增长发展,以后增长停止而进入稳定期,后者的增长也比前者要慢;非线性效应抑制了内波增长而使之趋于稳定,具有维稳作用。初始扰动在内波发展初期以线性模式演变为主,以后以非线性模式演变为主。

3)随着积分时间增加,线性情况下内波波包的波形大体不变,波包的正、负振幅大体相同,整个波包宽度也大体不变,仅振幅有所增长;非线性情况下内波波包的形状随积分时间发生改变,其正、负振幅之比越来越大,波峰前的陡降也越来越强。

4)线性情况下内波波包传播速度与其振幅无关,且传播速度大体不变;非线性情况内波传播速度与其振幅和波形有关,非线性效应越强,内波传播越慢。

5)从本文数值试验中海洋内波的波长、周期和传播速度来看,该内波属高频内波(短周期内波),性质为内重力惯性波。

因受篇幅限制,本文仅给出了一个个例的数值试验和分析结果,我们也曾对多个不同环境条件下的个例做过数值试验,得到了与本文大致相同的结果。另外,本文主要对高频内波(短周期内波)做了试验,未考虑其他内波的情况,数值模式中也未考虑海底地形,而实际海洋内波的发生演变环境场比较复杂,需进一步研究。

[1] FANG X H,DU T.Fundamentals of oceanic internal waves and internal wave in the China Seas[M].Qingdao:Ocean University of China Press,2005.方欣华,杜涛.海洋内波基础和中国海内波[M].青岛:中国海洋大学出版社,2005.

[2] CARL W.Internal tides in the ocean[J].Reviews of Geophysics,1975,13(1):167-182.

[3] LE L F,BEN J H.Some examples of detection of oceanic meso-scale eddies by the synthetic-aperture radar[J].Journal of Geophysical Research,1983,88(C3):1844-1852.

[4] STANTON T P,OSTROVSKY L A.Observations of highly nonlinear internal solutions over the continental shelf[J].Geophysical Research Letters,1998,25(14):2695-2698.

[5] MOUM J N,FARMER D M,SMYTH W D,et al.Structure and generation of turbulence at interfaces strained by internal solitary waves propagating shoreward over the continental shelf[J].Journal of Physical Oceanography,2003,33:2093-2112.

[6] NASH J D,MOURN J N.River plumes as a source of large-amplitude internal waves in the coastal ocean[J].Nature,2005,437:400-404.

[7] MACK A P,HEBERT D.Mixing structure of high frequency internal waves in the upper eastern equatorial Pacific[J].Journal of Physical Oceanography,1999,29:3090-3100.

[8] YUAN Y L,ZHENG Q A,DAI D J,et al.Mechanism of internal waves in the Luzon Strait[J].Journal of Geophysical Research,2006,111 (C11):1-9.

[9] YUAN Y L,WAN Z W,ZHANG Q H.A motion instability formation mechanism of the multi-core structure of the East China Sea Kuroshio[J].Science in China:Series D:Earth Sciences,2003,46(2):182-192.

[10] XU Z T.Oceanic internal wave dynamics[M].Beijing:Science Press,1999.徐肇廷.海洋内波动力学[M].北京:科学出版社,1999.

[11] ZHENG Q A,SUSANTO R D,HO C R,et al.Statistical and dynamical analyses of generation mechanisms of solitary internal wave in the northern South China Sea[J].Journal of Geophysical Research,2007,112,doi:10.1029/2006JC003551.

[12] LI D,CHEN X,LIU A.On the generation and evolution of internal solitary waves in the northwestern South China Sea[J].Ocean Modeling,2011,40(2):105-119.

[13] LI Q,FARMWR D M.The generation and evolution of nonlinear internal waves in the deep basin of the South China Sea[J].Journal of Physical Oceanography,2011,41:1345-1363.

[14] ZHANG M,ZHANG L F,AN J.Atmosphere spectrum analysis and unsteady I[M].Beijing:China meteorological Press,2008.张铭,张立凤,安洁.大气波谱分析及其不稳定性I[M].北京:气象出版社,2008.

[15] MU M.Nonlinear stability and instability of atmospheric motions[J].Bulletin of the Chinese Academy of Sciences,2001(6):432-435.穆穆.大气运动的非线性稳定与不稳定问题研究[J].中国科学院院刊,2001(6):432-435.

[16] ZHANG Y,ZHANG M.The numerical study of linear and nonlinear transversal unsteady[J].Journal of Meteorological Scince,1998,56 (4):447-457.张颖,张铭.线性和非线性横波不稳定的数值研究[J].气象学报,1998,56(4):447-457.

[17] DENG B,ZHANG M.Spectrum and spectral function analysis of wave in ocean Part I-mathematic model and numerical method[J].Chinese Journal of Hydrodynamics:Series A,2006,21(2):259-266.邓冰,张铭.海洋内部波动的波谱和谱函数I-数学模型和计算方法[J].水动力学研究与进展:A辑,2006,21(2):259-266.

[18] ZHANG X,DENG B,ZHANG M.Preliminary study of background current and topography effects on ocean internal wave[J].Marine Forecasts,2012,29(3):26-35.张翔,邓冰,张铭.背景流与地形对海洋内波影响初探[J].海洋预报,2012,29(3):26-35.

Numerical Experiments of Oceanic Internal Wave Evolution

DENG Bing1,ZHANG Yu-fei2,ZHANG Ming3
(1.Beijing Institute of Applied Meteorology,Beijing 100029,China; 2.College of Oceanic and Atmospheric Sciences,Ocean University of China,Qingdao 266100,China; 3.Institute of Meteorology and Oceanography,PLA University of Science and Technology,Nanjing 211101,China)

Numerical experiments of oceanic internal waves in pycnocline with background shear flow were conducted with two-dimensional non-hydrostatic linear and nonlinear numerical models.With the initial field and parameters prescribed by present study,it shows that he maximum density disturbance always appears within pycnocline,or captured by the pycnocline,consistent with in situ observations.In linear model, the stream function coincides with the density disturbance,with its negative/positive center corresponding to negative/positive center of the density disturbance,which is vertically distributed from ocean surface to bottom.The intensity of internal waves in linear model grows exponentially after adjustment period,and the background shear flow is unstable.But in nonlinear model,internal waves shows a quasi-linear development,then develop slowly till reaching a steady period.Thus the growing rate of internal waves in linear model is larger than that in nonlinear model,suggesting that the nonlinear effect reduces instability internal waves.As the integration of model continues,the shape of internal wave packet in the linear case is basically unchanged,except that the amplitude of internal waves increases.The propagation velocity of the wave packet is independent of its amplitude.But in nonlinear case,the shape of internal wave packet changes,and both its amplitude and the sudden fall before the wave crest increases consistently.The velocity of internal wave is related to its amplitude and wave shape,and the stronger nonlinear effect is,the more slowly the velocity of internal wave is.Based on the wave length,period and propagating velocity,the internal waves in the numerical experiments should be classified as high frequency inertial gravitational waves(or short-period waves).

numerical experiment;oceanic internal wave;pycnocline;background shear flow

P731.24

:A< class="emphasis_bold">文章编号:1

1671-6647(2017)01-0062-11

10.3969/j.issn.1671-6647.2017.01.007

2016-01-13

国家重点基础研究发展计划项目——西北太平洋海洋多尺度变化过程、机理及可预报性(2013CB956203)

邓 冰(1963-),女,江苏连云港人,高级工程师,博士,主要从事物理海洋学应用方面研究.E-mail:dbing039@163.com

Received:January 13,2016