浅析初中数学培养学生解题能力的有效措施

浙江省义乌市后宅中学 楼薇薇

浅析初中数学培养学生解题能力的有效措施

浙江省义乌市后宅中学 楼薇薇

例题作为检测学生学习情况以及教师课堂教学效果的最直接方式，当下已在实际课堂教材上被引进了教学的一部分，并加以延伸成了新型的例题教学方法。例题教学在初中数学课程教育中运用的比较普遍，例题教学能让学生有针对性地对具体知识点进行解读与分析，提高学生的学习效率，在具体的问题中将典型的问题结合所学知识点进行具体分析，可有效提升解题效率，也能深化对知识的了解程度，强化自身解题能力与综合分析能力。本文以浙教版初中数学教材为例，就如何有效培养学生解题能力的相关方法进行探讨和说明。

一、从抽象到具体

在培养学生解题能力的措施中，首先需要让学生形成从抽象到具体的思维方式，采用这种方式能够强化学生对题目的理解，有利于抓住题目中所给出的各项已知条件，进而加以灵活运用。尤其针对初中数学教学来说，课程内容所涉及的知识点较多，且对学生逻辑思维能力考查的范围较广泛，在学生对有关内容的理解时容易因想法偏差造成理解不透彻和不准确的情况，因此，强调学生的思维方法对提高学生的解题效率有很大帮助。通过将抽象题目的所给条件转化成为具体的已知内容，不仅能让学生充分把握题目要求，还能进一步强化学生对有关知识点的理解。

比如一些在创设情景基础之上的题目，教师在指导学生解决这类问题时要能够转化学生思考方式，让学生能够将题目中所给出的抽象问题进一步转变成具体的已知条件，从而对所学知识公式加以利用，完成解题。例如，假设有一个池塘，里面有无穷多的水。现有2个空水壶，容积分别为5升和6，如何只用这2个水壶从池塘里取得3升的水？在遇到这个问题时，所给出的条件都比较抽象，学生既不可通过实践操作来完成，也不能运用图形解决，那么就需要进行思维转化，此题就相当于是如何将数量分别为5和6的混杂体提炼出只有3，经过深入思考，我们可以得出，先用5升壶装满后倒进6升壶里，再将5升壶装满向6升壶里到，使6升壶装满为止，此时5升壶里还剩4升水，随后，将6升壶水全部倒掉，将5升壶里剩下的4升水倒进6升壶里，此时6升壶里只有4升水，再将5升壶装满，向6升壶里到，使6升壶装满为止，此时5升壶里就只剩下3升水了。在解决这类问题时，抽象的条件以及思考方法都很容易混淆学生思维，只要把握住严格按照题目要求和确定的解题方向为原则，才能确保解题的正确率。

二、数形结合

在学习初中数学函数方程以及平面直角坐标系等章节时会遇到许多数形结合的题目，在解答这类题目时，通常都要先画出与题相对应的图形，然后根据题目所给出的已知条件在图形中反映出来，进而利于学生理清自己的思路，以增强解决问题的效率和质量。此外，在数形结合的相关题目的解答过程中，涉及的理论知识较多，相关性质原理较宽泛，需要学生熟练掌握各项有关的性质定义，从而在实际解答过程中充分发挥作用。另外，在采用数形结合的解题思路解题时，还可结合题意恰当添加辅助线，通过增添辅助线的方式来作为挖掘题目潜在条件的方式。几种辅助线的添加方法要靠学生日常多积累和总结经验，要能够及时总结和归纳，进而增强和提高自己的解题速度。

比如：已知点C（2，3）,点B（0，1）,点A（2，0）。固定A．B两点不动,点C只能上下平移得到点D，求能使△ABD成为等腰三角形的点D坐标。如果在这个平面直角坐标系内有一点P（m，1/2），可以使△ABP的面积等同于△ABC，求m的值。根据题意，可先画图，然后再将已知条件在图形中反映出来，进而结合图形和实际问题加以深入探究。在求D点坐标时，由△ABD为等腰三角形可知AD=BD，则转化成了D点到A、B两点的距离相等，可根据此项性质列出方程式。通过观察图形，我们可以找出题目内的隐藏条件，若AD=AB，则AD=2√5，若AB=BD，作BE⊥AD，因为AB=BD，BE⊥AD，根据等腰三角形三线合一的性质，我们可以得出，AD=2AE=2×1=2。此外还有若AD=BD，则设AD长为x，由勾股定理可得：x2=22+（x-1）2，从而求得AD=5/2。另外，求m的值时，根据P（m，1/2）可列两个方程：当P位于第一象限时，有：m×1-1/2×1×2-（m-2）×1/2×1/2-1/2×1/2×m=3， 解 得 m=7；当P位于第二象限时，有：（2-m）×1-1/2×1×2-1/2×1/2× （-m）-1/2×1/2×（2-m）=3，解得m=-5。

三、分类讨论

最后，在分类讨论这类数学解题方法指导中，利用方程公式对未知数的取值范围进行探讨，可整合总结出最终的几个答案。比如有24个劳力种60公顷地，这块土地适宜蔬菜、棉花和小麦，对这三种农作物每公顷所需的劳力数及每公顷的收益预计如下：

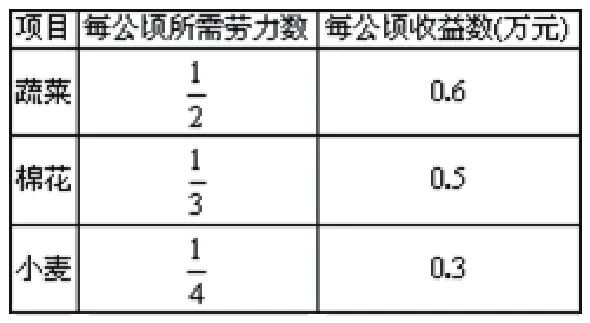
那么请你设计一种方案，使全部劳动力有活做，且总的收益最大，并求出这个最大值。这里，我们可以通过设未知数求解，设种蔬菜x公顷，种棉花y公顷，则种小麦（60-x-y）公顷。所以x×1/2+y×1/3+（60-x-y）×1/4=24， 解 得 y=108-3x， 所以种蔬菜x公顷，种棉花（108-3x）公顷，种小麦（2x-48）公顷，又0≤x≤ 60，0≤108-3x≤60，0 ≤2x-48≤60，解得24≤x≤36。设总收益为W万元，则W=0.6x+0.5（108-3x）+0.3 （2x-48）=0.6x+54-1.5x+0.6x-14.4=-0.3x+39.6。因为 W随x 的增大而减小，所以当x取最小值x=24时，W最大。所以这种方案为：种蔬菜24公顷，劳力12人；种棉花36公顷，劳力12人；种小麦0公顷，劳力0人。

综上所述，在初中数学培养学生解题能力时可以从以下几个方面进行，首先强调由抽象转变为具体的方法，揭示出实际例题的本质意义，然后充分利用数形结合解题的方法，通过增添辅助线等方法，在具体的例题教学过程中，教导学生灵活运用相关理论知识进行解题，让学生将所遇到的困惑列出来，教师就此进行针对讲解。最后，将教学知识点渗透进例题中，将例题解法与知识点结合到一起，从而达到深思提能的效果。善于引导学生多角度思考问题，转化多个思维多方面讨论。课后注意归纳和整理相关的解题方法，以进一步增强在课堂上的解题速度，取得优秀的成绩。在今后，我们还将不断深入研究解题方式的内部含义，为创设出更科学有效的教学方式以及培养出更多高质量人才和推进我国教学事业做努力。