股指期货对成分股和股指波动率的影响——使用面板GARCH模型和双重差分的分析

鹿 波

（北京金融衍生品研究院有限责任公司，北京100033）

一、前 言

本文使用面板GARCH模型和双重差分方法分析了股指期货对于现货市场波动率的影响。关于股指期货稳定市场的机理，从风险管理的角度来说有以下解释：股指期货为投资者提供了套取保值和避险的工具，在市场大幅下跌时，投资者通过股指期货规避系统性风险之后，反而会在现货市场买入超跌股票，从而起到稳定现货市场的作用。而上述作用的发挥需要股指期货市场具有足够的流动性，以吸收大额套保交易的价格冲击，不致于产生负反馈效应。股指期货限仓10手并提高保证金水平的措施大幅增加了投资者的交易成本，导致投资者减少交易甚至退出市场，股指期货市场的流动性水平大幅下降，吸收套保交易冲击的能力下降，最终影响股指期货稳定现货市场波动作用的实现。虽然不能获取市场中直接套保（对股指期货对应的股指及其成分股进行套保）和交叉套保（对股指期货对应股指以外的其他股指及其成分股进行套保）构成比率的数据，但是关于套保效率的研究基本上都是使用直接套保策略（张胜杰，2011；高扬，郭晨凯，2011；韩立岩，任光宇 2012；杜红军，王宗军，2013），因此可以合理推测市场中直接套保的比率要高于交叉套保，故而从风险管理的角度来说，股指期货降低相应股指波动率的作用要大于其他股指。

股指期货稳定市场还存在另外一个理论解释，即股指期货有助于抑制股市正反馈交易引起的波动。所谓正反馈交易指在证券价格上升时买进、价格下跌时卖出的一种交易行为，简单说就是“追涨杀跌”。相对于现货市场来说，股指期货市场交易效率高、价格变化迅速、正反馈交易现象并不显著，期现套利会使得现货市场价格走势与股指期货趋于一致，从而减少现货市场的非理性波动成分。另一方面，股指期货使得股市信息效率得到有效提升，即使没有套利交易，单纯通过价格信号的指引作用也会降低现货市场的正反馈交易。而管制措施减少了股指期货市场的流动性，进而信息效率下降，抑制现货市场正反馈交易的作用减弱，相应现货个股和指数的波动增加。无论是套利机制还是价格信号的指引机制，都是直接作用于股指期货所对应的现货股指，对于其他股指影响较小，因此从抑制股市正反馈交易的角度来说，股指期货降低相应股指波动率的作用也要大于其他股指。

关于股指期货稳定股市的理论解释还有流动性假说，即股指期货能够提高相应现货成分股的流动性（Silber，1985；Stoll和 Whaley，1985），增加其市场深度，从而降低现货成分股的波动率。从流动性的角度来说，股指期货降低相应股指及其成分股波动率的作用也要大于其他股指及其成分股。

实证中，为了剔除股指期货推出前后其他因素变化对于现货指数波动率的影响，我们使用双重差分方法，即以其他股指及其成分股的波动率作为其他影响波动率因素的代理变量，在此基础上考察股指期货覆盖的股票指数及其成分股的波动率的变化。从股指期货稳定股市的理论解释来看，股指期货降低相应股指及其成分股波动率的作用大于其他股指，如果假设除股指期货以外的其他系统性因素影响波动率相对差异的变化在我们考察事件前后没有差异①，则双重差分方法就能够从实证角度验证股指期货稳定股市的作用是否存在。

具体来说，首先以成分股的波动率减去非成分股的波动率，以考察股指期货对成分股波动率的影响。然后，使用面板GARCH和双重差分相结合的方法考察股票指数波动率的变化。即参考Cermeño和Grier（2006）以及陈海燕（2007）关于面板GARCH模型的估计方法，考察沪深300、中证500和中证1000三只股票指数的波动率分别受沪深300股指期货推出、中证500股指期货推出以及2015年9月份股指期货临时性管制措施三个关于股指期货的重大事件影响的情况。这三只股票指数的成分股互不重叠，共覆盖1800只股票，占到中国A股市场所有股票总数的2/3②。因此，三只股票指数具有较强的代表性。实证发现沪深300股指期货和中证500股指期货推出前后相应股票指数及其成分股的波动率相对于其他指数以及非成分股的波动率有明显的下降，而2015年9月的临时性管制措施出台前后，相应股票指数及其成分股的波动率则有所上升。上述实证结论从正反两方面验证了股指期货发挥稳定市场作用的机理。

本文的研究实现了以下创新。首先，将面板GARCH模型应用于股票指数波动率的研究，考虑了不同指数之间的条件相关性对于单个指数波动率的影响。其次，将面板GARCH模型和双重差分方法相结合，剔除了考察事件之外的其他因素对于波动率的影响，使得实证结果更有说服力。再次，首次应用面板GARCH模型和双重差分方法得到股指期货临时性管制措施对股票现货市场稳定性具有负面影响的结论。

本文结构安排如下。第一节中回顾相关文献，第二节介绍股指期货对成分股波动率的影响，第三节使用单变量GARCH模型和GARCH面板模型考察股指期货对股指波动率的影响，第四节是总结和政策建议。

二、文献回顾

关于影响我国股指波动率因素的研究有：徐炳胜（2007）研究金融政策对我国股市波动的影响，发现货币供应量、贷款余额、同业拆借利率对股市波动解释力不强，而离散性金融政策事件已成为我国股市短期波动的主要原因之一。罗曼丽（2014）提出影响我国股指波动性的因素有宏观经济、货币政策和股票市场制度三大因素，通过实证分析发现股票市场制度是我国股指波动的主要影响因素。张建波和李振（2014）使用6个行业的面板数据分析发现产品价格波动、产业集中度和行业市净率对某一行业总体的股票价格波动具有显著影响。

关于股指期货对于现货波动率的影响研究：涂志勇和郭明（2008）构建了一个多期多市场决策模型，由该模型预测股指在股指期货推出前短期上涨，推出后则下跌，并且股指期货的推出也可能降低市场的波动性。杨阳和万迪昉（2010）运用横截面分析和双重差分方法对股指期货上市对指数股和非指数股收益波动的影响进行分析，发现上市初期股票市场波动增大，随着有套取保值需求的特殊法人进入股指期货市场，指数股和非指数股的波动均显著降低，且指数股的降幅较大。许红伟和吴冲锋（2012）使用联立方程模型对股指期货推出一年内股票市场的流动性和波动性变化进行了考察，发现股票市场流动性下降、波动性上升。郦金梁，雷曜和李树憬（2012）使用EGARCH模型对2008年初至2011年10月的股指交易数据分析，发现沪深300股指期货推出后股指的条件方差下降了40%，并且市场深度提升，价格波动率的信息含量提高。Chen，Han，Li和Wu（2013）使用面板数据政策评估方法和几个主要国际市场股票指数月度波动率的面板数据对没有股指期货交易情况下的沪深300股票指数波动率进行预测，并与实际的波动率进行比较，发现实际波动率大约低19%。郑振龙，郑国忠，张亦春（2014）也对股指期货的推出对现货市场质量的影响进行了综合考察，使用基于马尔科夫转换的随机波动率（MSSV）模型对沪深300股指期货推出前后的波动率变化进行了分析，并与使用GARCH、EGARCH、随机波动率（SV）方法得到的结果进行比较，发现股指期货推出之后现货市场波动率呈现下降态势。Xie和Mo（2014）使用双重差分的方法考察2005年5月至2012年12月沪深300成分股相对于非成分股波动率的变化，发现沪深300股指期货推出之后的几个月这种相对波动率有所上升，但长期来看并没有影响。

实证方法方面，我们参考了两类文章，分别是关于面板GARCH和双重差分的文章。樊智和张世英（2003）针对多元GARCH模型提出了基于遗传算法的似然估计方法。Cermeño和Grier（2006）提出了存在条件方差和协方差关系的动态面板GARCH模型的估计方法，并使用DPDCCV模型对G7的月度通货膨胀率进行考察，发现高通货膨胀率是较难预测的，没有证据支持关于通货膨胀率的高不确定性会产生高通货膨胀率的说法。Cermeño和Grier（2006）的估计方法适用于横截面数据较小而时间序列数据较多的面板数据，正好适用于我们所使用的数据。 陈海燕（2007）、Lee（2010）和申敏等（2013）分别使用面板GARCH模型进行相关研究。双重差分方面，Tang和Xiong（2012）使用双重差分的方法发现2000年以来美国非能源类商品期货的价格与原油价格的相关性增强，而且这种相关性在两个流行商品指数包含的商品中更加明显。

三、股指期货对成分股波动率的影响

首先考察股指期货对股票指数成分股波动率的影响。由于中证指数公司定期（半年）和不定期对上述指数成分股进行调整，本文根据相关调整公告对成分股做出相应的调整，以保证不同时间区间本文考察的指数成分股与实际保持一致。

（一）波动率差值

首先计算每只股票某个月份股票日收益率的方差，代表该股票在该月份的波动率。然后，计算成分股以及非成分股两组股票在该月份波动率的中位数③。最后，将两组股票的波动率中位数相减得到中位数差值。沪深300成分股和非成分股的结果如图1所示。图1中上方标注三角的曲线即沪深300股票指数成分股与非成分股波动率中位数的差值④。横线代表2005年7月至2010年3月中位数差值的均值。2010年4月之后中位数差值大多低于横线的数值，只是股指期货推出初期和2014年11月至2015年1月之间出现了异常升高。股指期货推出初期，股指期货对于现货市场影响较小，指数成分股可能仍然保持原来的波动率分布；而2014年底沪股通开通之后，在境外投资者对A股投资的建仓期，指数成分股受到的关注高于非成分股，导致波动率差值出现短期性上升。对沪深300股指期货推出前后中位数差值进行Z检验和秩和检验⑤，发现Z值分别为-3.65和-3.48，表明沪深300股指期货的推出显著降低了指数成分股的波动率。此外，从图1还可看到2015年9月之后中位数差值相比之前有所上升，表明临时性管制措施对于沪深300成分股波动率具有不利影响。

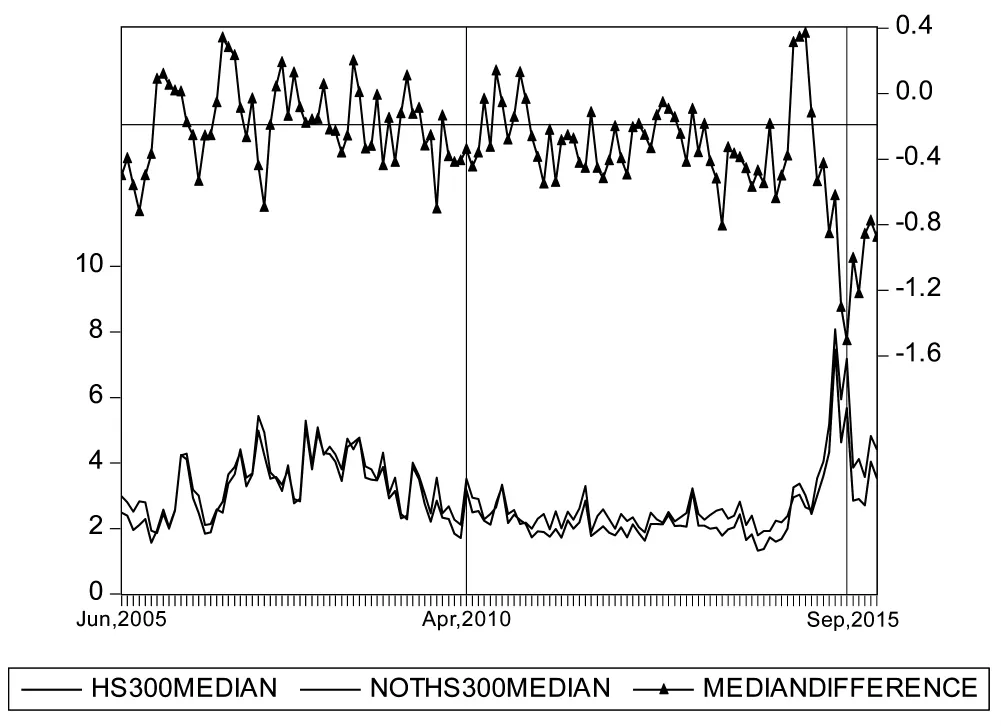
图1 沪深300成分股与非成分股波动率差值的变化（2005年6月-2016年1月）

中证500成分股和非成分股的波动率如图2所示。以剔除沪深300和中证500成分股之外的其他股票代表中证500的非成分股。图2中横线代表2011年1月至2015年3月中位数差值的均值。从图2可以看到，2015年4月以后中证500成分股的相对波动率出现了明显下降，Z检验和秩和检验的值分别为-7.32和-4.50，差异非常显著。

（二）面板数据的双重差分

成分股波动率的变动还可以通过面板数据的双重差分回归进行考察。对于沪深300成分股和非沪深300成分股来说，假设：σ2it=C1+C2*I201004+C3*I1*I201004。其中i=1、2，分别代表沪深300成分股波动率中位数和非沪深300成分股波动率中位数；I201004为虚拟变量，在沪深300股指期货推出之前取数值0，推出之后取数值1；I1代表沪深300成分股，即如果是沪深300成分股波动率的中位数则取值为1，否则取0。同理假设：σ2jt=C4+C5*I201504+C6*I2*I201504。其中j=1、2，分别代表中证500成分股波动率中位数和非中证500成分股波动率中位数；I201504在中证500股指期货推出之前取数值0，推出之后取数值1；I2代表中证500成分股，即如果是中证500成分股波动率的中位数则取值为1，否则取0。

实证结果为 C1=3.29，C3=-0.38，C4=2.91，C6=-0.48，除 C6 之外其余系数均在5%显著水平下显著。这表明，沪深300股指期货推出之后沪深300成分股的相对波动率显著下降了11.55%（C3/C1），中证500股指期货推出之后中证500成分股的相对波动率下降了16.49%（C6/C4）。

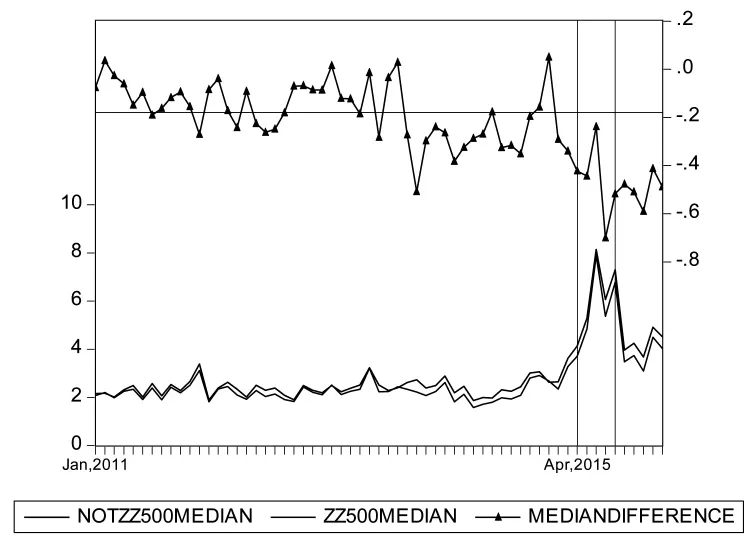
图2 中证500成分股与非成分股波动率差值的变化（2011年1月-2016年1月）

四、股指期货对股指波动率的影响

下面考察沪深300、中证500和中证1000股票指数的波动率。虽然上证50股指期货也已于2015年4月15日上市，但是由于上证50股票指数的成分股完全包含在沪深300股票指数成分股当中，无法区分沪深300股指期货和上证50股指期货对上证50股票指数波动率的影响，因此实证当中不再考察上证50股票指数。

（一）单变量GARCH模型

在引入面板GARCH模型进行分析之前，我们首先假设三只股票指数之间不存在条件相关性，即使用单变量GARCH模型考察某一股票指数波动率随时间的变化情况。假设三只股票指数的收益率满足GARCH（1，1），由此可以得到每只股票指数的条件方差σ2it。使用双重差分方法对σ2it进行实证分析，即假设：

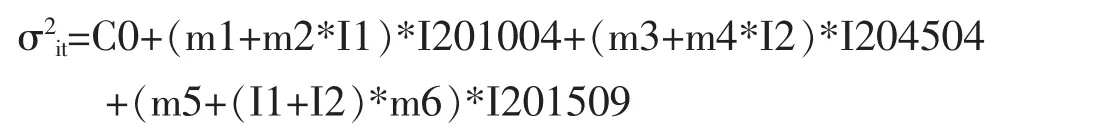
其中i=1，2，3，分别代表沪深300、中证500和中证1000股指的条件方差。I201004、I201504、I1和I2的含义与前文相同，I201509代表管制措施的实施，实施之前取值0，实施之后取值为1。使用2006年4月至2016年4月日度收益率的实证结果为m2=-0.0000826，m4=0.000152，m6=-0.000289，且均在1%显著水平下显著。因此不考虑股票指数之间条件相关性的情况下，沪深300股指期货的推出降低了相应指数的波动率，中证500股指期货的推出增加了相应指数的波动率，而股指期货的管制措施减少了股指期货所覆盖指数的波动率。但是从后面的分析可以看到，不考虑股票指数之间的条件相关性并不是一个合理的选择。

（二）面板GARCH模型

1.模型的一般形式及其识别

（1）模型的一般形式

r1t、r2t和r3t分别代表沪深300、中证500和中证1000股票指数的收益率。关于收益率rit、条件方差σ2it和条件协方差σijt的面板GARCH模型：

在时间序列方向有足够样本的情况下，均值方程的残差项渐进服从正态分布。因此，我们可以使用极大似然法对模型参数及其标准差进行估计。模型的条件对数似然函数可表示为：

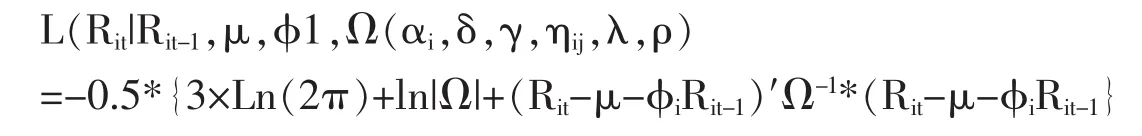
其中Rit=（r1t，r2t，r3t）′。使用极大似然估计方法就可以求出模型参数及其标准差，初始值使用GARCH-BEKK模型估计得到的参数⑥。

（2）模型识别

使用上述模型计算对数似然函数的工作量很大，因此在正式求解之前，对模型的恰当形式进行预先识别是有必要的。准备工作包括两部分：一是识别均值方程的最优模型。二是识别条件方差和条件协方差方程的最优模型。

（a）均值方程的识别

我们使用三只股票指数2006年4月至2016年4月的日度收盘价数据，时间序列方向有超过2000个样本，最小二乘估计量是渐进一致的。因此均值方程估计使用LSDV估计量⑦和HAC协方差矩阵⑧。关于均值方程截距项μi的沃德检验χ2（2）=0.346，84.12%的概率不能拒绝原假设。因此，截距项个体效应不显著。关于自回归系数φi的沃德检验χ2（2）=5.344，5%显著水平下不能拒绝原假设。因此自回归系数不存在个体效应。

（b）条件方差和条件协方差方程的识别

条件方差和协方差方程识别包括判断截距项（αi、ηij）是否存在个体效应以及 ARCH 项（δ、λ、γ、ρ）的形式。

截距是否存在个体效应可以通过检验均值方程的残差平方自回归的截距项和残差交叉乘积自回归的截距项是否存在个体效应来确定。此外，还可以通过检验均值方程是否存在无条件异方差作为补充检验方法，如果存在无条件异方差，则条件方差就可能存在个体效应。残差平方自回归截距项的沃德检验χ2（2）值为5.209，在5%的显著性水平之下不能拒绝原假设。均值方程无条件异方差似然比检验的χ2（2）=28.76，拒绝原假设。因此条件方差有可能存在个体效应。残差交叉乘积自回归截距项的沃德检验χ2（2）值为3.955，不能拒绝原假设。似然比检验所得到的χ2（2）=26.46，拒绝原假设。因此条件协方差也有可能存在个体效应。

为了确定方差协方差过程是否受时间序列的影响，可以检验均值方程的残差平方和残差交叉乘积是否表现出明显的自相关模式。⑨依据偏相关系数显著的阶数不同，可以对条件方差协方差的方程形式进行选择。如果只有一阶滞后显著，则可以使用ARCH（1）过程，多阶滞后显著，则可以使用GARCH（1，1）过程。通过残差平方对其滞后1至10阶序列的AR（10）混合回归，发现除第5、6、9阶滞后项之外，其余均显著。因此，条件方差使用GARCH（1，1）过程。通过对残差交叉乘积的AR（10）混合回归，发现也是除了第5、6、9阶滞后项不显著之外，其余滞后项均显著。因此，条件协方差方程也使用GARCH（1，1）过程。

（3）识别结果

根据模型识别的结果，均值方程不存在个体效应，条件方差和条件协方差方程采用GARCH（1，1）过程，截距项是否存在个体效应并不确定。因此，依据条件方差和条件协方差方程截距项是否存在个体效应，模型取四种形式：

模型一

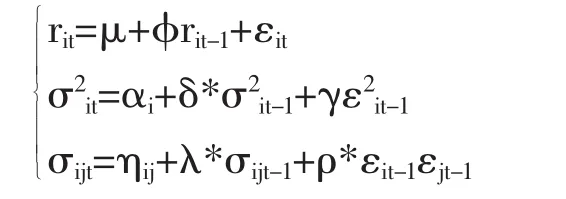
模型二

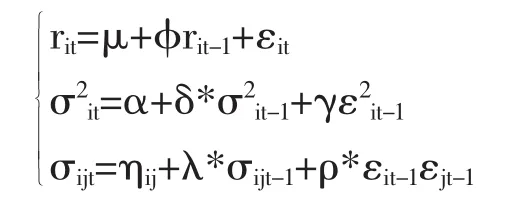
模型三

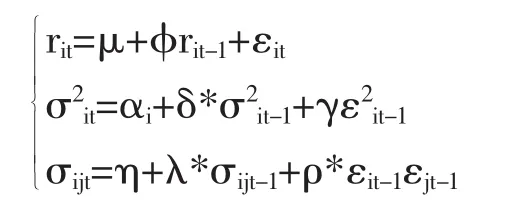
模型四

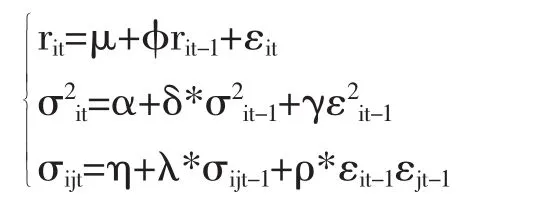
其中 Eit|Φt-1～N（0，Ωt），Eit=（ε1t，ε2t，ε3t）。

模型一的波动率方程既考虑了条件方差的个体效应，又考虑了条件协方差的个体效应；模型二只考虑了条件协方差的个体效应；模型三只考虑了条件方差的个体效应；模型四则均未考虑条件方差和条件协方差的个体效应。

2.双重差分的虚拟变量

为了剔除其他因素对于股指波动率的影响，同样需要在面板GARCH模型中采用双重差分的方法。为了达到这一目的，我们在条件方差方程中添加虚拟变量，即假设：

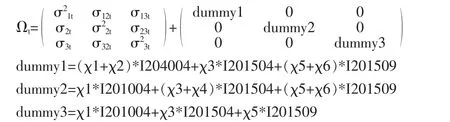
其中I201004、I201504和I201509的含义与前文相同。x1代表沪深300股指期货推出之后非沪深300股票指数波动率的变化，x1+x2代表沪深300股指期货推出之后沪深300股票指数波动率的变化，因此x2代表剔除其他因素之后，沪深300股指期货的推出对于沪深300股票指数波动率的影响。同理，x4代表剔除其他因素之后，中证500股指期货的推出对于中证500股票指数波动率的影响；x6代表剔除其他因素之后，股指期货管制措施对于股指期货覆盖的股票指数波动率的影响。因此，我们主要考察χ2、χ4和χ6，即剔除其他因素影响之后，股指期货重大事件对相应股指波动率的影响。

3.实证结果

智能分析仪表端能产生的预警信号包括： 计算出试剂等消耗品余量值、余量不足、消耗品用完。例如硅表试剂还剩3 d的余量时，产生预警信号，给予用户充足的时间增补试剂。系统能给用户提供相应的处理参考方法。

使用三只股票指数2006年4月20日至2016年4月5日的收盘价数据，并取对数差分代表收益率。每只股票指数共有2421个日度收益率数据。实证结果如表1所示。简洁起见，未给出条件方差和条件协方差方程ARCH项的系数。

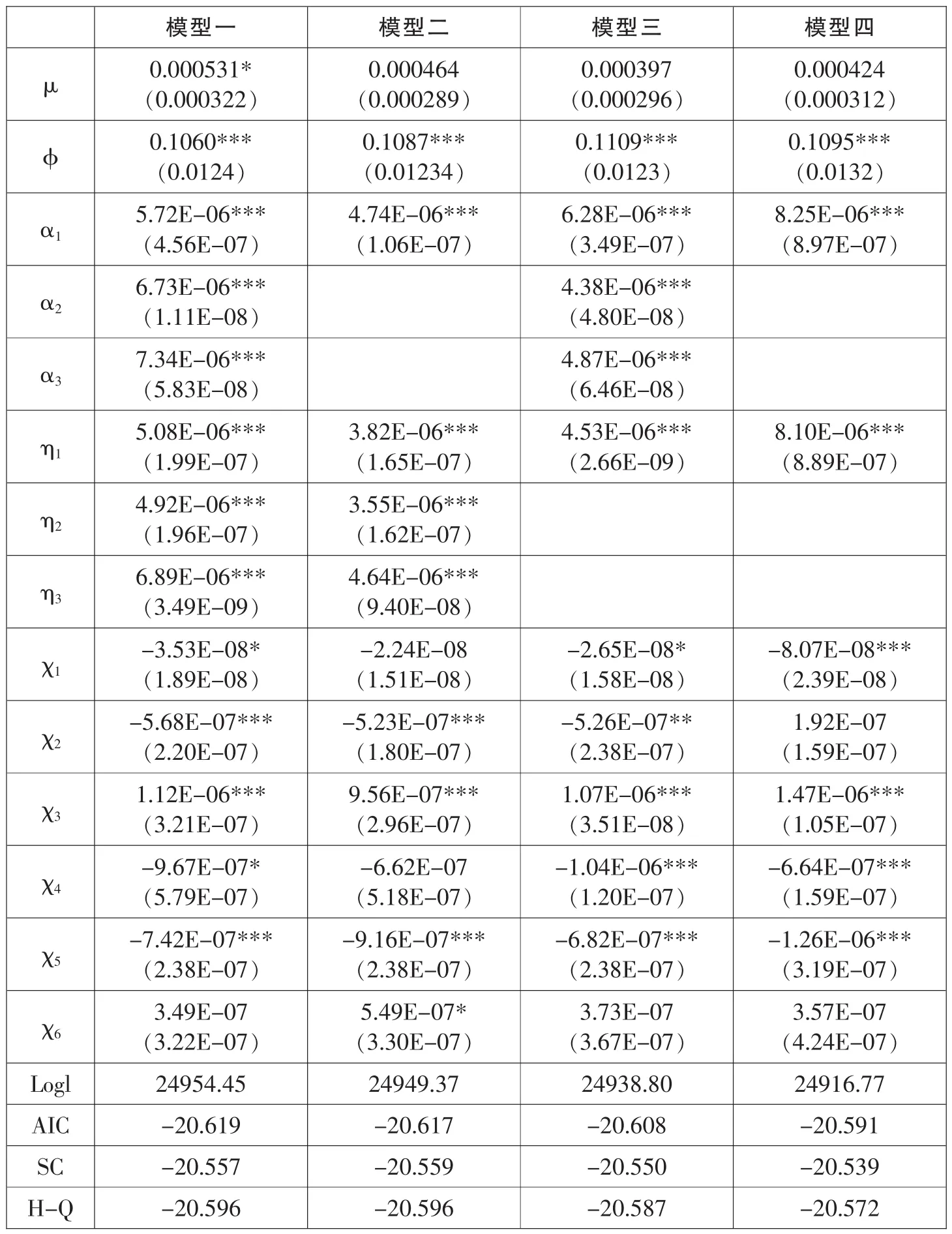
表1 股指期货对股指波动率的影响

从表1可以得出以下结论：

第一，股指期货的推出降低了相应股票指数的波动率。首先，沪深300股指期货的推出显著降低了沪深300股票指数的波动率。从模型一可以看到，沪深300股票指数的波动率降低了，即 χ2/α1）。 其次，中证500股指期货的推出也显著降低了中证500股票指数的波动率。这与不考虑条件相关性时的结论不同。从实证结果来看股票指数收益率之间的条件相关性显著为正，且具有较强的时变特征（图3）。从图3可以看出中证500股指期货推出之后股指收益率之间的条件相关性迅速上升，即股价进入同涨同跌模式，因此考虑中证500指数与沪深300和中证1000指数收益率的条件相关性之后，中证500指数的相对条件方差在中证500股指期货推出之后不升反降。从模型一可以看到，中证500股票指数的波动率降低了14.37%（χ4/α2）。

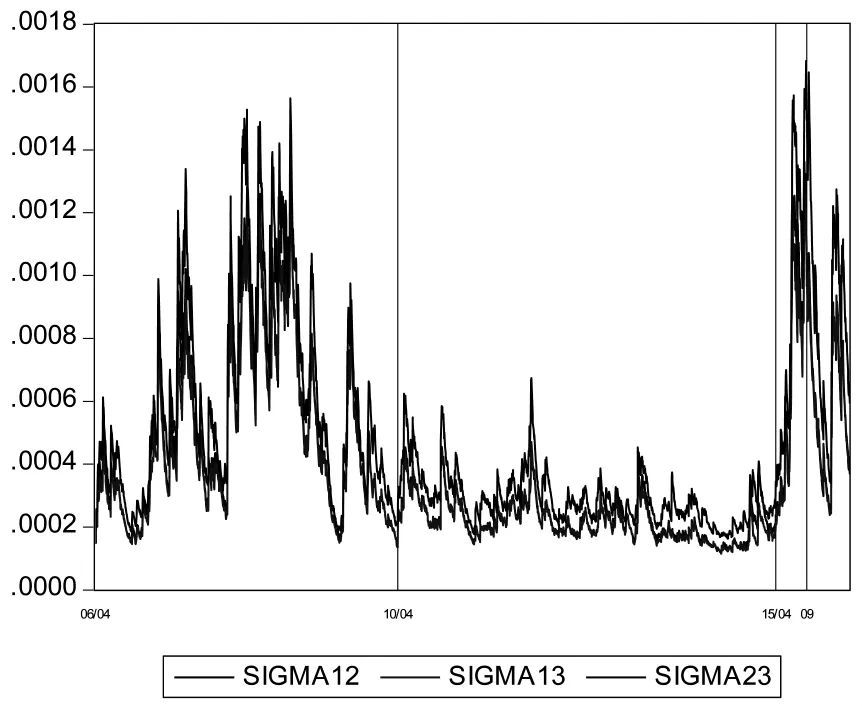
图3 沪深300、中证500和中证1000的条件协方差（2006年4月-2016年4月）

第二，2015年9月的临时性管制措施导致了相应股票指数波动率的提高。虽然临时性管制措施对沪深300股票指数和中证500股票指数的波动率产生的影响并不显著，但四个模型都表明沪深300股票指数和中证500股票指数的波动率确实出现了上升迹象。这与未考虑条件相关性时的结论也有所不同。以模型一为例，沪深300股票指数的波动率上升了6.10%（χ6/α1），中证500 股票指数的波动率上升了 5.19%（χ6/α2），平均上升了 5.61%（χ4/［（α1+α2）/2］）。从实际情况来看，股指期货限制性措施实施以来，市场连续大幅下跌的情况并没有消失，反而屡次出现，这从一定程度上可以说明是由于股指期货稳定市场的作用下降导致的。

第三，股指期货之外的其他因素对股指波动率也有影响。首先，沪深300股指期货推出之后中证500和中证1000股票指数的波动率下降了0.5%（χ1/［（α2+α3）/2］）。 其次，中证 500股指期货推出之后，沪深 300和中证 1000股指波动率显著上涨了 17.15%（χ3/［（α1+α3）/2］）。 再次，股指期货临时性管制措施出台之后中证1000股指波动率显著下降了10.11%（χ5/α3）。由此，沪深300股指期货推出之后其他影响因素导致市场波动率下降，中证500股指期货推出之后其他影响因素导致市场波动率上涨，股指期货临时性管制措施出台之后其他影响因素导致市场波动率下降。如果按照传统的方法，只以事件发生之后单一股指波动率变化作为衡量股指期货对股市波动率影响的标准，则会得出中证500股指期货增大股指波动率、股指期货临时性管制措施降低股指波动率的误导性结论。而表1已将其他影响因素剔除，并且考虑了条件相关性，由此发现中证500股指期货降低了相应股指的波动率，而管制措施提高了相应股指的波动率。

五、总结和政策建议

从上述实证分析看出，股指期货的推出确实有助于降低相应股指及其成分股的波动率。而2015年9月份实施的管制措施则增大了股指及其成分股的波动率，不利于市场稳定。因此，应当尽快取消临时性管制措施，恢复正常交易，促进股指期货稳定现货市场功能的发挥。

注释:

① 波动率在股指期货推出前后相对差异的变化不能完全排除其他系统性因素的影响，但是本文的模型一和模型三均考虑了条件方差的个体效应，而考虑面板数据的横截面固定效应相当于考虑了不同指数横截面的不同特征（如平均市值不同）对波动率的影响，即控制了不同横截面特征对波动率的影响。因此，双重差分中的处理组和控制组排除了由于内在固有个体差异所造成的影响。

② 截至2016年4月20日，中国A股市场股票总数为2838只。

③ 分析数据发现波动率均值与波动率中位数两种指标的走势大致相同，但是均值差值较易受到异常值的影响而导致在部分区间差异较大，因此采用中位数指标更加合理一些。

④ 该波动率差值与沪深300波动率中位数在全样本的相关系数为-0.012，P值为0.89；在沪深300股指期货推出之前的相关系数为0.22，P值为0.09；在2015年9月份管制措施实施之后的相关系数为0.58，P值为0.31。只是在沪深300股指期货推出之后至管制措施之前的一段时间内相关系数为-0.30，P值为0.02，主要原因是股市波动迅速上升时，波动率差值呈明显下降态势，这正表明了股指期货能够降低相应成分股的波动率，不可将波动率差值变动的原因归于波动率差值与波动率的负相关关系。

⑤ z检验和秩和检验都是用来比较两个样本差异性的方法，不同的是Z检验假设样本服从正态分布，而秩和检验不对样本分布有要求，只是使用样本排序的数值代替实际值。使用两种方法同时进行验证的目的是提高结论的稳健性。

⑥ GARCH-BEKK 模型假设 Ωt=Ω*Ω′+B*Ωt-1*B′+A*Et-1*Et-1′+A′，Ω 为下三角矩阵。 在假设面板GARCH模型dummy1、dummy2和dummy3的初始值为0的情况下，其他参数的初始值可以由GARCH-BEKK模型估计得到的Ω、B、A的数值计算得到，其中αi和ηij由Ω计算得到，δ和λ由Β得到，γ和ρ由Α得到。

⑦ 即虚拟变量最小二乘估计量。

⑧ 即异方差自相关一致的协方差矩阵。

⑨Bollerslev（1986）建议对残差的平方进行检验，以确定是否具有条件异方差效应。

［1］陈海燕.随机影响变截距面板 GARCH（1，1）模型及其应用［J］.数量经济技术经济研究，2007，24（1）：143-150.

［2］杜红军，王宗军.基于 Copula-CVaR 模型的股指期货套保比率度量［J］.管理评论，2013，25（4）.

［3］樊智，张世英.多元GARCH建模及其在中国股市分析中的应用［J］.管理科学学报，2003，6（2）：68-73.

［4］高扬，郭晨凯.不同策略下沪深300股指期货套期保值有效性研究［J］.证券市场导报，2011（8）：31-35.

［5］韩立岩，任光宇.基于已实现二阶矩预测的期货套期保值策略及对股指期货的应用［J］.系统工程理论与实践，2012，32（12）：2629-2636.

［6］郦金梁，雷曜，李树憬.市场深度、流动性和波动率——沪深300股票指数期货启动对现货市场的影响［J］.金融研究，2012（6）：124-138.

［7］申敏，邓晓卫，奚陵.货币政策对房价及其波动的动态影响——基于协整关系的面板GARCH模型［J］.数学的实践与认识，2013，43（16）：18-26.

［8］涂志勇，郭明.股指期货推出对现货市场价格影响的理论分析［J］.金融研究，2008（10）：104-116.

［9］许红伟，吴冲锋.沪深300股指期货推出改善了我国股票市场质量吗——基于联立方程模型的实证研究［J］.南开管理评论，2012，15（4）：101-110.

［10］杨阳，万迪昉.股指期货真的能稳定市场吗?［J］.金融研究，2010（12）：146-158.

［11］张建波，李振.行业因素对我国股票价格波动率的影响研究［J］.山东大学学报：哲学社会科学版，2014（1）：88-93.

［12］张胜杰.考虑交易成本的套期保值策略选择研究［J］.云南财经大学学报：社会科学版，2011（3）：71-74.

［13］郑振龙，郑国忠，张亦春.日内信息结构、羊群行为及风险异化［J］.证券市场导报，2014（8）：53-59.

［14］罗曼丽.影响我国股指波动性主要因素研究［D］.中国农业大学，2014.

［15］徐炳胜.中国股市波动的金融政策解释［D］.复旦大学，2007.

［16］Cermeño R， Grier K B.Conditional heteroskedasticity and cross-sectional dependence in panel data： an empirical study of inflation uncertainty in the G7 countries［J］.Contributions to Economic Analysis， 2006， 274： 259-277.

［17］Chen H， Han Q， Li Y， et al.Does index futures trading reduce volatility in the Chinese stock market?A panel data evaluation approach［J］.Journal of Futures Markets， 2013， 33（12）：1167-1190.

［18］Lee J.The link between output growth and volatility： Evidence from a GARCH model with panel data［J］.Economics Letters， 2010， 106（2）： 143-145.

［19］Tang K， Xiong W.Index investment and the financialization of commodities［J］.Financial Analysts Journal， 2012， 68（5）： 54-74.

［20］Xie S， Mo T.Index Futures Trading and Stock Market Volatility in China： A Difference‐in‐Difference Approach［J］.Journal of Futures Markets， 2014， 34（3）： 282-297.

［21］Silber W L.The economic role of financial futures［M］.Salomon Brothers Center for the Study of Financial Institutes， Graduate School of Business Administration， 1985.

［22］Stoll H R， Whaley R E.The new option markets［M］.University of Alberta.Institute for Financial Research，1985.