基于改进SVD-Prony算法的永磁同步风力发电机参数辨识

刘 洋，蔺 红，晁 勤

(新疆大学电气工程学院，新疆 乌鲁木齐 830001)

由于永磁同步风力发电机具有功率因数高、效率高和易于精确定位控制等优点，永磁同步风力发电机被广泛应用大型风力发电机、高性能精确伺服中［1-3］。发电机参数(电阻、电感、磁链)是分析电力系统电磁暂态和机电暂态计算和控制的基础数据，由于缺少准确的实际参数，造成计算结果与实际工况不符，严重影响计算的准确性和可信度［4］，因此精确捕获永磁同步风力发电机参数的重要性显得越来越突出［5-6］。

国内外专家对发电机参数辨识进行了大量的研究。由于三相短路电流中存在基波和谐波分量，各分量的变化规律由发电机的参数决定［7-8］，因此有文献采用发电机定子侧三相短路试验获取三相短路电流的方法进行参数辨识，文献［9］采用最小二乘法对三相短路的双馈式异步风力发电机进行参数辨识;文献［10］采用全局最优位置变异PSO优化算法对三相短路的双馈式异步风力发电机参数进行分步辨识，但都不适用于辨识永磁同步风力发电机参数。文献［11-13］分别采用快速傅里叶变换算法(FFT)、神经网络算法、粒子群算法对永磁同步电机进行参数辨识，但未采用短路试验法。文献［14-16］利用Prony算法的辨识精度高、辨识速度快且能够在线辨识等优点，并各自增加滤波方法、小波预处理、神经网络算法等改进措施抑制噪声干扰，但辨识的是低频振荡参数，而不是永磁同步风力发电机参数，且不能准确确定拟合模型的阶数，影响了参数辨识的准确度。

本文针对以上问题，建立了永磁同步风力发电机定子侧三相短路电流的辨识模型，提出改进SVDProny辨识算法，达到了去除噪声且能确定拟合模型阶数的效果，采用FFT法将三相短路电流分解成基波和谐波两个分量，通过改进SVD-Prony算法辨识出各电流分量对应的特征量，进而辨识出永磁同步风力发电机参数，对2种类型的算例准确辨识出了永磁同步风力发电机参数，并仿真验证了本文辨识方法的可行性、模型的有效性以及辨识的参数准确性。

1 参数辨识模型

采用文献［17］给出了永磁同步风力发电机的数学模型

式中，ud、uq、id、iq分别为定子端电压和电流的d轴和q轴分量，可以直接测量获得;ω为定子电角速度，ω=npωr，其中np为发电机转子极对数，ωr为转子转速可以测得，则ω可以计算得到;L为定子等效电感;ψ为永磁体磁链;R为定子绕组电阻，R，L，ψ是可辨识的。

对式(1)进行简化

永磁同步风力发电机定子侧三相短路过程可以分解为两种状态:

(1)短路前的稳定运行状态。此时di/dt=0，即式(2)左端为0，在此条件下求解式(2)并经坐标变换后得到稳态运行时发电机定子A相电流表达式为

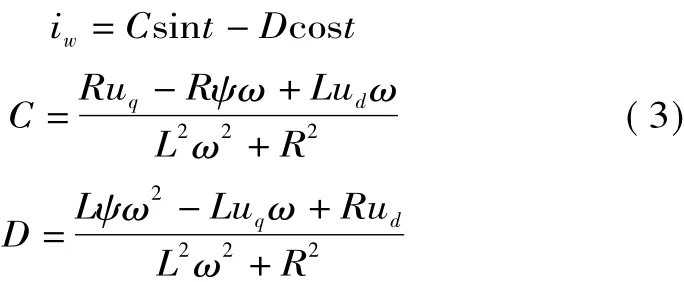
(2)定子端突然加上与短路前端电压大小相等方向相反的三相电压状态。此时对式(2)进行拉氏变换可以求得定子电流复频域的解

式中，s为拉普拉斯算子;I0为初始电流;E为单位矩阵。由于定子突然加反向电压，则初始电流为0，接着进行拉氏反变换可以得到在d、q轴中定子电流的时域解，对其进行坐标变换并与式(3)叠加可以得到网侧三相短路时发电机A相电流的辨识模型

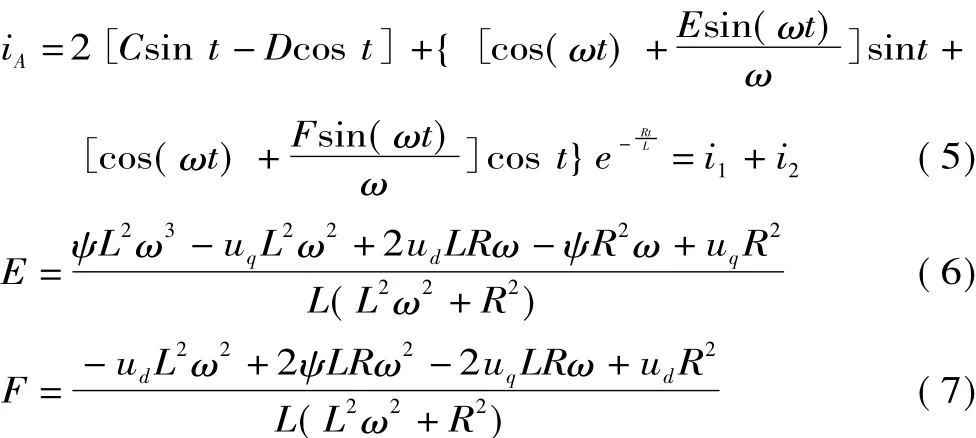
式中，i1为不衰减的基波分量;i2为衰减的谐波分量;C、D、E、F是辨识模型的特征量，经过辨识算法得到特征量，将其代入式(3)、(6)，即可得到所要辨识的参数。设置永磁同步风力发电机参数(标幺值)为:R=0.011 62，L=0.378，ψ=1.215，ω=3.5，ud=1，uq=1。将参数代入式(6)形成的辨识模型电流与将参数代入搭建的Simulink仿真模块中生成的短路电流如图1所示。

对图1a、1b两图对比可以得到，两种方法得到的电流波形相同，验证了辨识模型的正确性。

2 改进SVD-Prony辨识算法

2.1 SVD算法

设观测信号为x(n)(n=0，1，…，N－1)，其中N为采样点总数。将x(n)构造为矩阵X，为使SVD分解具有一定的抗噪声能力，L常取N/4～N/3。则观测信号矩阵X为

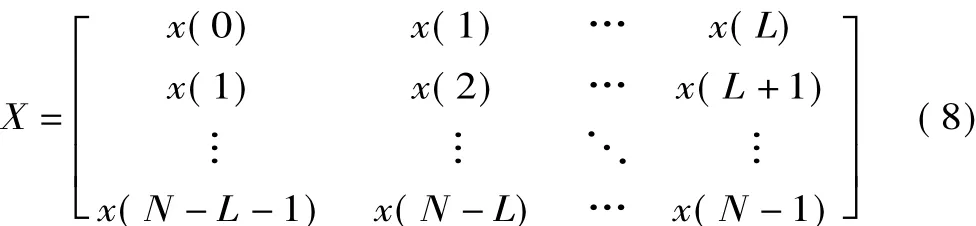
对X进行SVD分解

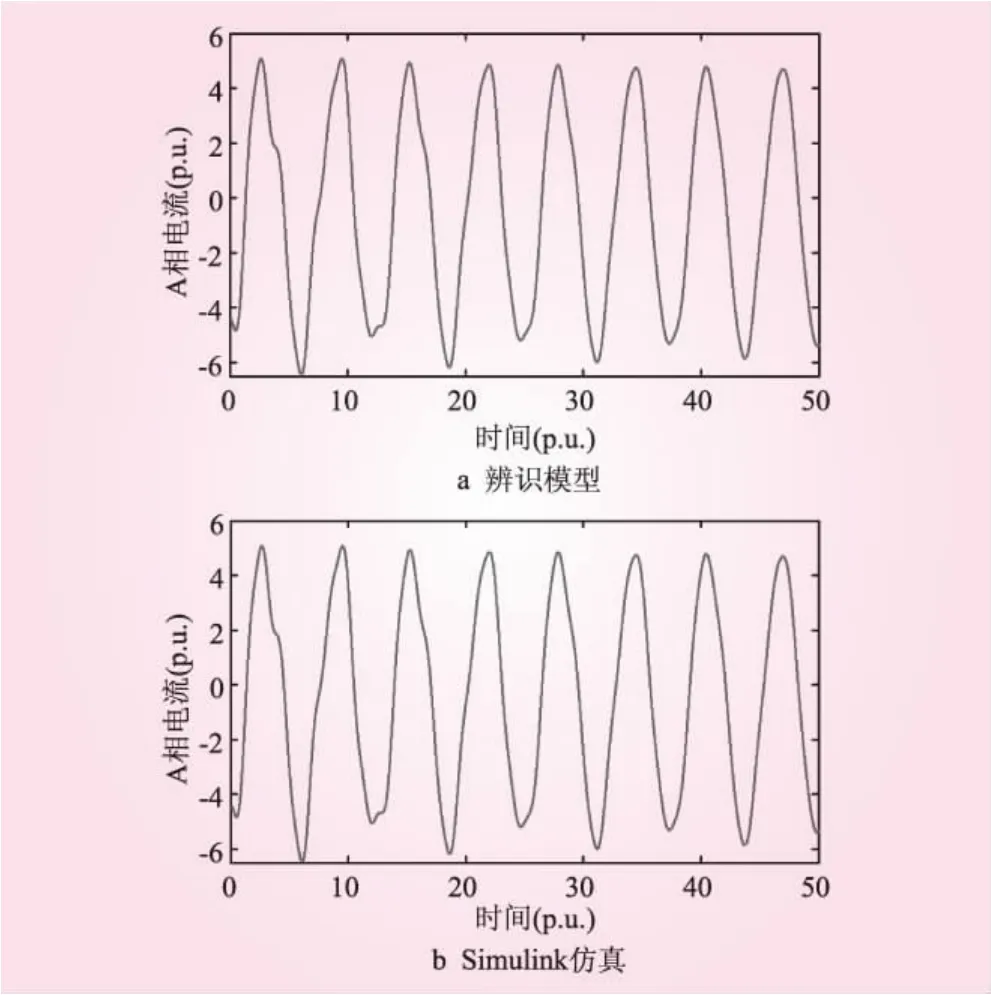
图1 电流波形比较

式中，X为(N－L)×(L+1)维复数矩阵，U和V分别为(N－L)×(N－L)维和(L+1)×(L+1)维酉阵，上标*表示矩阵的共轭，∑是奇异值矩阵，主对角元素是奇异值σ，奇异值中包含了X矩阵秩的特性信息。

2.1.1 消除噪声

观测信号x(n)中包含真正信号及噪声信号，利用SVD算法对其分解如式(8)，其中较大的奇异值反映了真实信号，较小的奇异值则反映噪声信号，将小于奇异值均值的奇异值置零，再进行SVD反变换重构观测信号就可以去除信号中的噪声，还可保留观测信号的基本特征不变。

2.1.2 计算阶数

定义Frobenious范数意义上可最佳逼近X的矩阵

式中，∑k是∑中k个较大的奇异值构成的对角阵。X(k)逼近X的程度可用逼近性能测度表示:

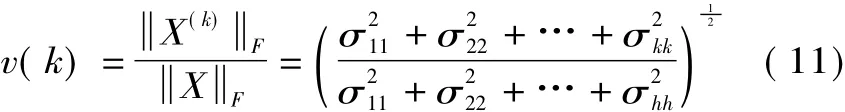
为了很好地表征矩阵特性，常取一个非常接近1的数作为阈值，然后设定k的初值，计算v(k)，若v(k)小于选取的阈值，则增大k值，直至v(k)大于该阈值，从而确定了矩阵X的有效秩，即拟合模型阶数。

2.2 改进SVD-Prony算法

Prony算法用一组具有任意振幅、相位、频率、衰减因子的复指数函数的线性组合近似拟合观测信号x(n)，改进SVD-Prony算法拟合模型为其中，k为拟合模型有效阶数，由SVD算法确定，N为采样点总数，bm和zm为复数。

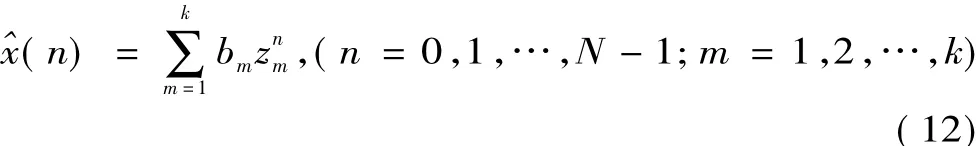
构造k×(k+1)的去噪后的R矩阵

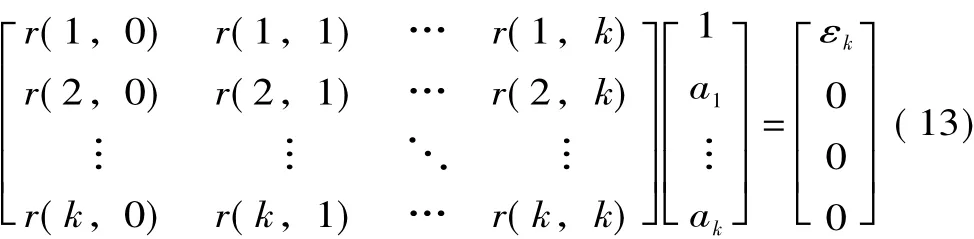
其中am(m=1，2，…，k)为特征多项式系数。R矩阵中的各元素为

求解式(11)可得am，将am代入特征多项式方程

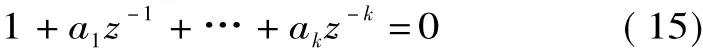
解得特征多项式的根zm，将zm代入式(10)中可求得参数bm，获得改进SVD-Prony拟合模型。

2.3 改进SVD-Prony算法求拟合模型步骤

(2)计算有效阶数k:设阈值为0.998，给定秩k的初值，根据SVD算法计算有效阶数k。

(3)构造去噪后的R矩阵:根据式(12)求得R矩阵的各元素，构造出去噪后的R矩阵。

(4)确定改进 SVD-Prony拟合模型:根据式(12)～(15)求解特征多项式的系数a、特征根zm、参数bm，得到改进SVD-Prony拟合模型。

3 参数辨识实现及误差评价

3.1 参数辨识实现

(1)采样永磁同步风力发电机定子侧三相短路短路电流，利用FFT变换将电流分解为基波以及谐波分量，用每个分量确定改进SVD-Prony算法的关键指标:模型阶数 k、采样时间间隔 Δt、采样点数N。

3.2 误差评价

当原始参数未知或者观测信号并非理想信号时，一般用信噪比SNR来衡量辨识误差，SNR值越高，则误差越小，辨识参数的精确性越好。信噪比定义为

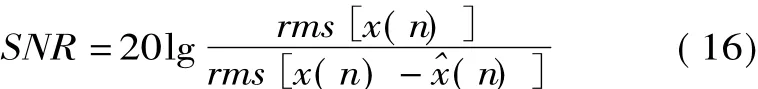
式中，rms为均方根;SNR单位为dB。

百分比误差表示辨识参数值与参数准确值之间差值与参数准确值的百分比，PE值越小，则误差越小，辨识精度越高。百分比误差定义为

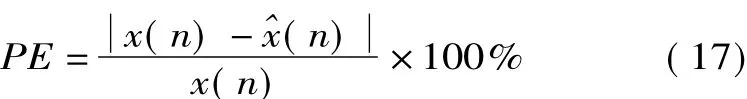
当PE＜10%或者SNR＞20 dB时，辨识结果可以接受;当SNR＞40 dB时，辨识结果更为理想。

4 算例及仿真

4.1 算例1(基于辨识模型的带噪声观测信号)

为了验证本文提出的改进SVD-Prony算法能够有效辨识永磁同步风力发电机参数，对一台参数已知的发电机进行仿真，设置发电机参数(标幺值)为:R=0.011 62、L=0.378，ψ =1.215，ω =3.5，ud=1，uq=1。根据式(5)构造已知参数观测信号，如图1(a)所示。通过文献［4］中提出的确定最佳采样间隔与采样点数方法，确定当采样间隔Δt=2.5 ms、采样点数N=250时，拟合效果最好。

在已知参数观测信号中加入高斯白噪声(如图2a)生成带噪声的已知参数观测信号如图2(b)所示，从图中可以看到，加入高斯白噪声后在局部改变了理想信号的波形，必然会对参数的精确辨识造成干扰。

由改进SVD-Prony算法计算出的基波拟合模型有效阶数k为32，谐波的拟合模型有效阶数k为33。

用传统Prony算法以及改进SVD-Prony算法进行参数辨识，参数辨识结果(标幺值)如表1所示。

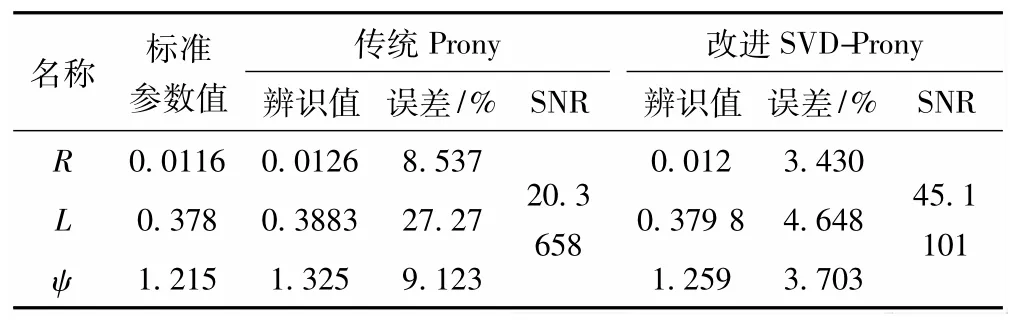
表1 有噪声影响辨识的参数

从表1中看出:在有噪声干扰的情况下，采用传统Prony算法辨识参数，PE最高误差达到27.27%，SNR为20.3658dB，参数辨识精度较低;采用本文提出的改进SVD-Prony算法辨识参数，PE的最大误差仅为4.648%，SNR为45.110 1 dB，参数辨识的精度较为理想。

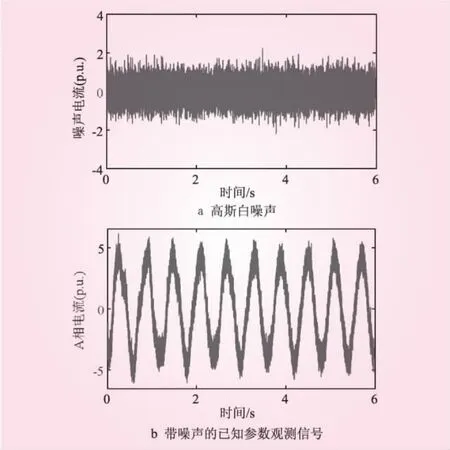
图2 加噪声的观测信号

分别将改进SVD-Prony算法与传统Prony算法辨识的参数代入辨识模型，生成的观测信号与不带噪声的已知参数观测信号拟合波形如图3所示。从图3中可以看出，传统Prony算法辨识参数生成的观测信号偏差较大，而改进的SVD-Prony算法辨识参数生成的观测信号偏差较小。

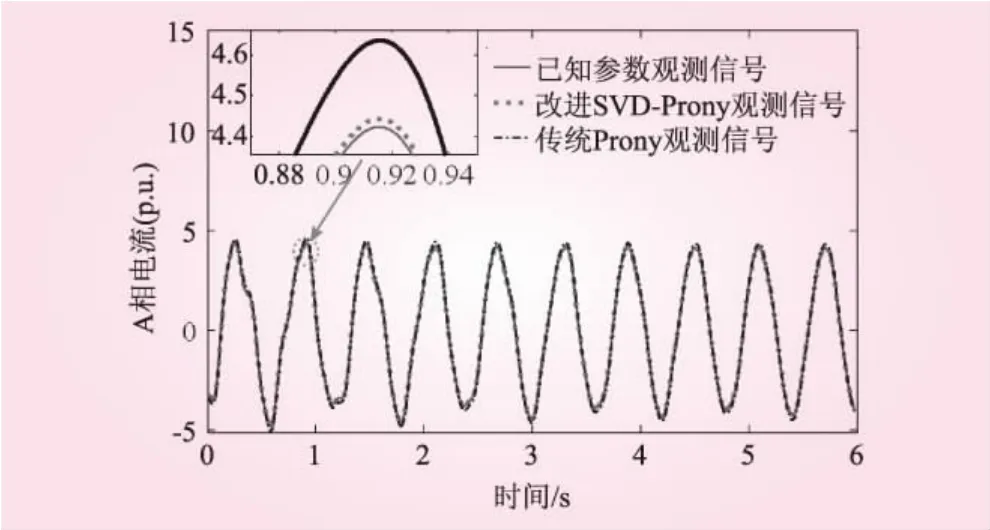
图3 拟合波形

从表1和图3中可以看出本文提出的改进SVDProny算法去噪效果好，辨识的参数较精确。

4.2 算例2(基于Simulink仿真波形)

利用Matlab/Simulink搭建永磁同步风力发电机与电网的仿真模型。设置发电机参数为:R=0.01 Ω，ψ=0.175 Wb，L=0.003 H，发电机出口电压为690 V，经过机侧变压器升压为35 kV，后经输电线路送往220 kV变电站。时间为0.5 s时发生三相短路故障，故障电流波形如图4所示。

由改进SVD-Prony算法计算出基波拟合模型有效阶数k为9，谐波的拟合模型有效阶数k为3。

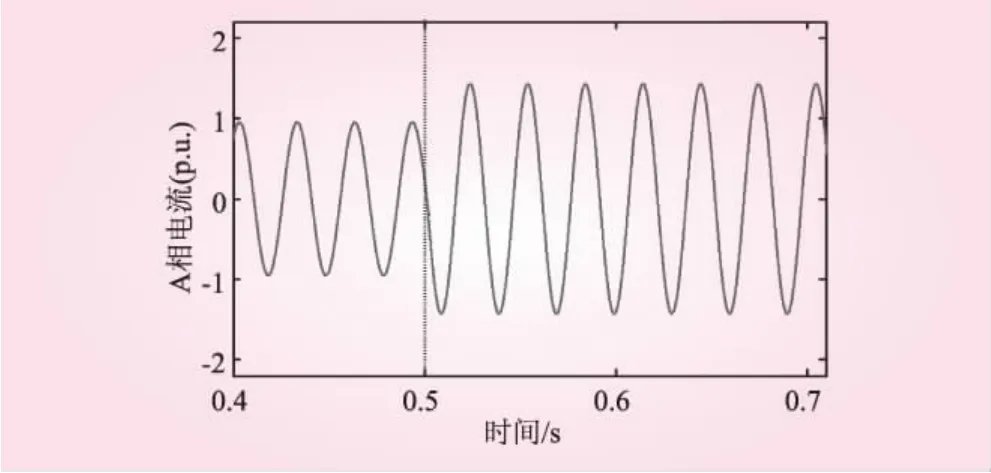
图4 故障电流波形

用改进SVD-Prony算法进行参数辨识，参数辨识结果(标幺值)如表2所示。

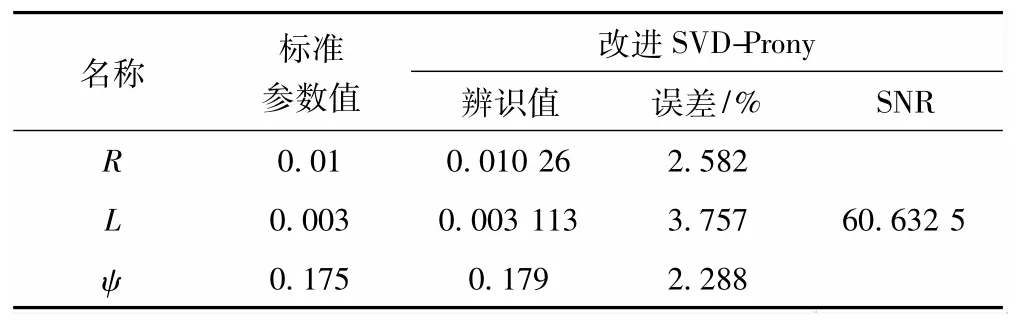
表2 仿真中辨识的参数

从表2中可以看出，采用改进SVD-Prony算法辨识的参数PE皆小于5%，SNR达到了60.632 5 dB，辨识结果较为理想。将辨识参数代入辨识模型生成的观测信号与采集的观测信号拟合波形如图5所示。从图5中发现改进SVD-Prony算法具有很高的参数辨识精度，满足在线辨识的要求。

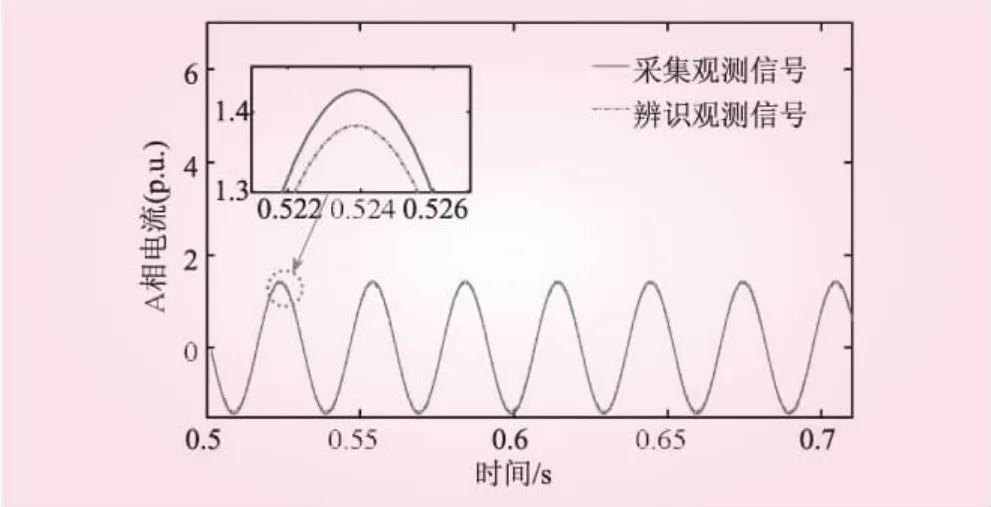
图5 改进的SVD-Prony算法拟合的波形

5 结论

依据永磁同步风力发电机定子侧三相短路电流的基波和谐波分量变化规律由发电机参数决定的特征，建立了发电机定子侧三相短路时短路电流的辨识模型。并在传统Prony算法基础上进行了改进。通过对加入噪声的观测信号和搭建的仿真模型进行参数辨识，结果表明改进SVD-Prony算法在噪声影响和在线条件下皆能较为准确地辨识发电机参数，且比传统Prony算法辨识准确度更高、抗噪性能更好。

［1］康劲松，劳建忠．直驱型风力发电系统中永磁同步发电机的控制技术研究［J］．机电一体化，2010，17(8):13-17．

［2］刘侃，章兢．基于自适应线性元件神经网络的表面式永磁同步电机参数在线辨识［J］．中国电机工程学报，2010，30(30):68-73．

［3］周义杰，年珩．变流器单边可控下开绕组永磁同步发电机的控制技术［J］．电工技术学报，2015，30(10):123-130．

［4］苏小林，周双喜．Prony法在同步发电机参数辨识中应用［J］．电力自动化设备，2006，26(9):1-4．

［5］肖曦，许青松，王雅婷，等．基于遗传算法的内埋式永磁同步电机参数辨识方法［J］．电工技术学报，2014，29(3):21-26．

［6］金宇清，赵泽，鞠平．双馈感应风力发电机的参数辨识分析［J］．高电压技术，2011，37(7):1700-1705．

［7］李兴源，朱瑞可，王渝红，等．基于EMD和Prony算法的同步电机参数辨识［J］．电网技术，2012，36(8):136-139．

［8］张建华，陈星莺，刘皓明，等．双馈风力发电机三相短路分析及短路器最大电阻整定［J］．电力自动化设备，2009，29(4):6-10．

［9］张建华，辛付龙，陈星莺，等．双馈风力发电机三相短路状态下的参数辨识［J］．电力自动化设备，2012，32(6):86-89．

［10］潘学萍，鞠平，徐倩，等．双馈风力发电机参数分步辨识及观测量的选择［J］．中国电机工程学报，2013，33(13):116-126．

［11］RAHMAN K M，HITI S．Identification of machine parameters of a synchronous motor［J］．IEEE Transactions on Industry Applications，2005，41(2):557-565．

［12］LIU K，ZHANG Q，CHEN J T，et al．Online multiparameter estimation of nonsalient-pole PM synchronous machines with temperature variation tracking［J］．IEEE Transactions on Industrial Electronics，2011，58(5):1776-1788．

［13］傅小利，顾红兵，陈国呈，等．基于柯西变异粒子群算法的永磁同步电机参数辨识［J］．电工技术学报，2014，(5):127-131．

［14］李大虎，曹一家．基于模糊滤波和Prony算法的低频振荡模式在线辨识方法［J］．电力系统自动化，2007，31(1):14-19．

［15］任子晖，刘昊岳，徐进霞．基于小波变换和改进Prony方法的电能质量扰动分析［J］．电力系统保护与控制，2016(9):122-128．

［16］竺炜，唐颖杰，周有庆，等．基于改进Prony算法的电力系统低频振荡模式识别［J］．电网技术，2009，33(5):44-47，53．

［17］蔺红，晁勤．并网型直驱式永磁同步风力发电系统暂态特性仿真分析［J］．电力自动化设备，2010，30(11):1-5．