基于动力系统反演理论的马斯京根流量演算误差校正
2017-03-20梁忠民王旭伟宁亚伟李彬权胡义明
梁忠民,王旭伟,宁亚伟,王 军,李彬权,胡义明
(河海大学水文水资源学院,江苏 南京 210098)
0 引言
马斯京根法(以下简称“马法”)物理概念明确,已在世界上众多河流的洪水演算中得到了广泛应用[1]。马法误差的来源包括输入项误差(即上断面及区间入流误差)、模型本身误差(即模型结构及参数估计误差)[2-3]。目前对参数估计误差的研究较多,一般可通过试错法、最小二乘法、非线性规划法以及一些智能算法等[4-8],得到模型的最优参数估计值,以提高演算精度,但关于马法中输入项误差的研究相对较少。而水文系统是一个由许多变量组成的复杂的非线性系统,具有时变、空间分布不均和不确定性等特点[9]。尽管采用完整的动力模型描述水文系统存在困难,但这些模型一般存在一系列特解,这就是多年的观测资料[10]。因此,只要能利用观测资料求解出与数值求解相反的问题,就可以反演出能近似描述水文动力系统运动方程的非线性模式[11-12]。
基于上述思想,本文应用系统反演理论,建立马法中上断面入流项、区间输入项及模型系统本身误差的非线性反演方程,对各误差进行校正,从而构建基于系统反演理论的马法演算误差校正方法,以提高河道下断面水文要素的预报精度。将该方法应用于淮河中游润河集站的洪水预报,取得了较好的预报效果。
1 模型构建
考虑区间入流的马法演算方程可表示为

式中,t+Δt为给定预报时刻;It、It+Δt分别为河道上断面的实测和预报流量;Qt、Qt+Δt为下断面的实测与预报流量;qt+Δt为区间预报流量;K为蓄量关系曲线的坡度;X为流量比重系数。
It+Δt和 qt+Δt一般是通过某种方法预报获得的,因而不可避免地存在预报误差。该误差又会在马斯京根方程演算过程中传递给Qt+Δt,同时马斯京根法本身也存在误差;从而使得最终的预报结果会有一定误差。为了降低最终预报结果的误差,本文根据动力系统反演理论构建上述各项误差的反演方程,分别对其进行校正,以提高“水资源高效开发利用”研究项目的预报精度。
1.1 动力系统反演理论
状态随时间而变的系统称之为动力系统,可由特定的方程(如微分方程)表示。动力系统的反演就是由观测资料反求描述动力系统方程的过程[9]。水文系统的发展变化受多种因素的影响[13-15]。以一个含有3个水文变量x,y,z的系统为例,构建以下方程组来描述系统的运动。即
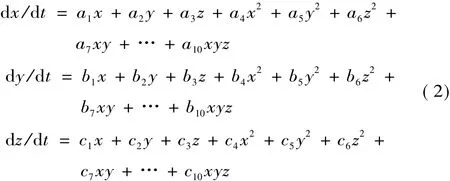
若把系统中变量x随时间的变化作为研究对象,对于上述方程组中的第一个方程,虽然参数a1,a2,a3,…,a10都是未知的,但可从观测资料中找到该方程的特解,同时对上述的微分dx/dt取差分形式则可得到在t时刻的反演方程

若观测数据时间序列长度为n,则对每一个时刻都有上述的方程,合并这些方程便可建立下列的反演方程矩阵

式中,M为变量矩阵;A为系数向量;Δt是时间间隔;n是时间序列的长度。
利用向量的最小二乘估计,即残差平方和极小化方法[16-17],可求出系数向量
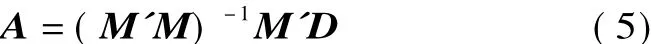
具体应用时,一般可剔除A中一些系数贡献非常小的项,以相对方差作为剔除依据[16]。即

对Wk小于某一规定值的系数项,予以剔除。
1.2 马斯京根演算误差的动力系统反演校正
根据式(1),马法预报结果Qt+Δt的误差来源可分为三部分:It+Δt的误差的误差方程本身的误差考虑上述三种误差的马斯京根方程下断面预报出流的校正值为
式中,M'为M的转置矩阵。

因此,根据t时刻及其之前时刻水文变量的实测值和预报值,按式(1)~式(6)可以构造误差的反演方程,据此计算t+Δt时刻相应的误差值,再由式(7)计算下断面预报流量的校正值。

对式(8)中误差的微分用差分格式代替,则有
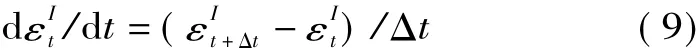
将式(9)代入式(8)得
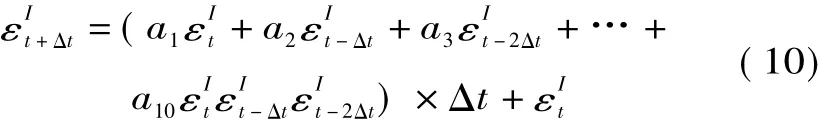
根据式(10)即可得到上断面入流项的误差校正结果;同理,亦可建立区间入流项及马法模型本身误差的反演方程。但区间流域往往缺乏实测洪水数据,这时可以将该两项误差合成(记为ε't+Δt),统一进行系统反演。由式(1)可知

根据历史场次洪水数据以及相应的区间预报值,得到误差 ε't+Δt时间序列,参照式(10)建立其反演方程

求得式(10)的系数向量A和式(12)的系数向量A'后,即可计算出误差再根据式(7) 进行下断面预报值的修正,从而实现马法的动力系统反演校正预报。
2 应用研究
2.1 研究区概况
选用淮河流域润河集站为研究站点,对本文方法进行应用检验。淮河润河集站位于淮河中游,控制流域面积40 360 km2。润河集站断面的洪水来源分为五部分:淮河干流王家坝、官沙湖分洪道钐岗、洪河分洪道地理城、史河蒋家集以及上述入流断面与润合集之间的区间流域入流。流域水系概化如图1所示。
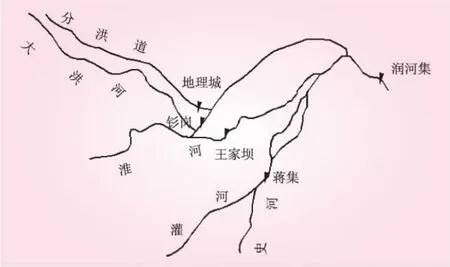
图1 淮河润河集站控制断面流域水系概化
2.2 方法应用
根据淮河流域2004年至2010年的观测数据,采用“先合后演”的马法对润河集站进流量预报,即根据新安江模型预报润合集上游4个站的入流(限于篇幅预报结果略,下同),再合成作为上游河道的总入流;区间入流亦采用新安江模型进行预报,并作为旁侧入流加入马法演算,从而得到润合集断面流量过程(见表1~3);其中,根据河道洪水传播特性,预报时间步长Δt取10 h。
根据已有研究成果[18],确定采用的马法参数为:x=0.087;K=50.7;C0=0.012;C1=0.183;C2=0.805。选用6场洪水资料对反演方程的参数进行率定和检验,其中3场用于反演方程参数向量A和A'的率定,3场进行验证。参数A和A'的率定结果分别见表1和表2,校正前后场次洪水精度统计结果见表3,其中两场洪水校正前后过程线对比如图2所示。

表1 反演方程系数向量A的率定结果

表2 反演方程系数向量A'的率定结果
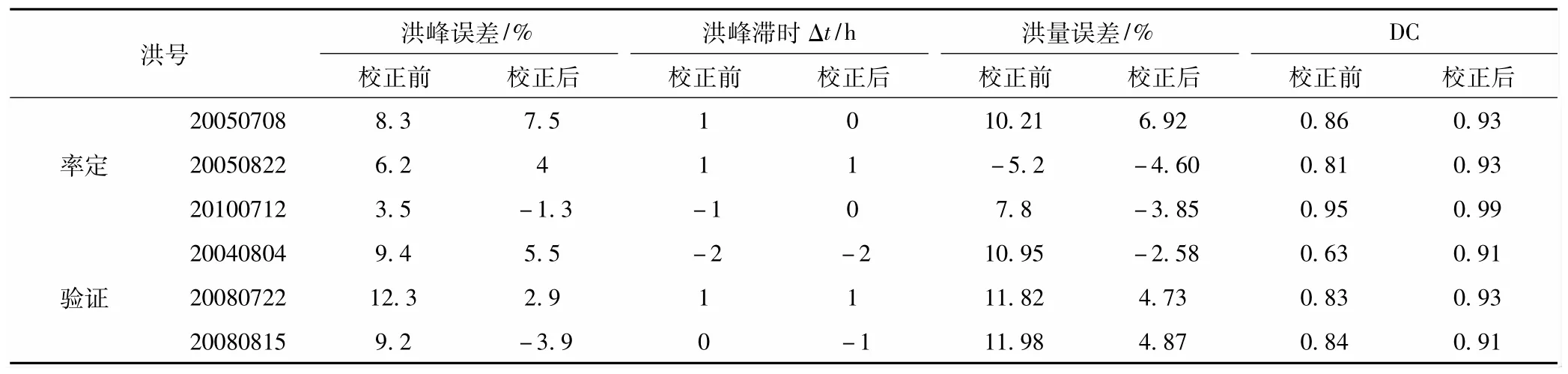
表3 淮河润河集站场次洪水马法演算及校正结果

图2 淮河润河集站洪水马法演算校正前后对比
从表3及图2以看出,马斯京根法较适合于研究区河道的洪水演算,6场洪水校正前的峰/量误差都在15%以内,确定性系数平均达0.80以上;但经过动力系统误差反演校正后,精度可进一步提升,其中峰、量误差均在10%以内,确定性系数在0.90以上。另外,校正前后洪峰滞时差异不甚明显,综合比较而言,校正后的预报精度有较明显提高。
3 结论
本文提出了一种基于动力系统反演的马法河道洪水演算校正新方法,并以淮河干流润河集站为例进行了研究,主要结论如下:
(1)马法河道洪水演算中可能存在三类误差。即,上断面入流项I(t+Δt)的预报误差、区间入流项q(t+Δt)的预报误差以及马法本身模型的误差;动力系统反演作为一种从特解去归纳出系统方程的方法,可用以构建马法误差项的反演方程,实现各项误差的实时校正,从而提高洪水预报精度。
(2)对淮河干流润合集站的应用结果表明,按系统反演技术建立的误差校正模型,可有效降低洪水演算误差,峰量相对误差在10%以内,确定性系数达0.90以上,预报精度有较明显提升。
(3)本文以马法为例构建了基于系统反演的预报校正方法,但方法的思路亦可应用于其他水文预报的实时修正问题。
[1]王家彪,雷晓辉,廖卫红,等.马斯京根模型改进新思路[J].南水北调与水利科技,2016,14(2):87-92.
[2]罗军刚,解建仓,张刚.洪水演算的参数自适应马斯京根法[J].水力发电学报,2011,30(3):57-64.
[3]沈丹丹,包为民,刘可新,等.马斯京根汇流参数抗差估计研究[J].中国农村水利水电,2016(7):72-74.
[4]李小波.多元优化算法在马斯京根模型参数优化中的应用[J].水资源与水工程学报,2016,27(5):158-161.
[5]黄清烜,梁忠民,曹炎煦,等.基于误差修正的BP神经网络含沙量预报模型[J].水力发电,2013,39(1):23-26.
[6]张新明,马艳.马斯京根模型参数反演的改进粒子群算法[J].哈尔滨工程大学学报,2016,37(2):271-277.
[7]程银才,王军,李明华.基于改进模式搜索法的马斯京根法模型参数率定方法[J].水电能源科学,2016(9):4-15.
[8]张悦,李国芳,吴洁,等.基于改进二分法的马斯京根法入流过程反演分析[J].水电能源科学,2015(3):44-47.
[9]张晓伟.水文动力系统自记忆特性及其应用研究[D].西安:西安理工大学,2009.
[10]黄建平,衣育红.利用观测资料反演非线性动力模型[J].中国科学:化学,1991,21(3):331-336.
[11]张文华.用非线性槽蓄方程进行洪水演进计算[J].水利学报,1965(1):41-42.
[12]丁晶,王文圣,赵永龙.反演水文动力模型的探讨[J].水力发电学报,2002(3):7-11.
[13]TANG X N,KNIGHT D W,SAMUELS P G.Volume conservation in variable parameter Muskingum-Cunge method[J].Journal of Hydraulic Engineering,1999,125(6):610-620.
[14]KIM J H,GEEM Z W,KIM E S.Parameter estimation of the nonlinear Muskingum model using harmony search[J].Journal of the A-merican Water Resources Association,2001,37(5):1131-1138.
[15]TAKEUCHI K,AO T,ISHIDAIRA H.Introduction of block-wise use of TOPMODEL and Muskingum-Cunge method for the hydroenvironmental simulation of a large ungauged basin[J].Hydrological Sciences Journal,1999,44(4):633-646.
[16]林振山.非线性科学及其在地学中的应用[M].北京:气象出版社,2003:141-147.
[17]芮孝芳,蒋洪庾.基于时间序列分析最优控制理论的洪水演算方法[J].水利学报,1993(4):41-47.
[18]水利部淮河水利委员会.淮河流域淮河水系实用水文预报方案(上)——淮河干流及支流主要控制站[M].济南:黄河出版社,2002.
