基于LH-OAT与变异系数法的汇流模型参数敏感性分析

李 昂，祝雪萍，武鹏林

(太原理工大学水利科学与工程学院，山西 太原 030024)

0 引言

流域汇流模型是广泛应用于洪水预报系统中的预测工具［1］。各地区根据本地降雨径流情况，研制了各种用于洪水预报的汇流模型。但在实际汇流过程中，由于模型结构的简化和随机性因素的影响，使得确立模型参数的工作量加大，模型参数误差增加，无法精确评价汇流模型各参数的重要性及贡献率，不能保证模型的运行效率和模拟精度。因此，有必要对汇流模型的参数进行敏感性分析。

目前，多数流域水文模型参数敏感性分析多集中在产流模型上，常用的分析方法有扰动分析法、Monte Carlo法、Latin-Hypercube模拟法、随机OAT法以及LH-OAT等。而关于汇流模型参数敏感性的分析比较少见，多数是对参数的优化和改进。周明等［2］对计算瞬时单位线汇流参数m1公式进行了非线性改进;何书会等［3］以纳什瞬时单位线的基本原理为基础，结合当地实测资料，提出了河北地区的汇流参数计算公式;金林［4］运用地貌参数确定了纳什单位线汇流参数，解决了山西省缺乏地区汇流资料的问题。

本文以山西省洪水预报系统中的纳什瞬时单位线汇流模型为研究对象，通过运用LH-OAT敏感性分析法，对汇流模型中所涉及到的参数进行敏感性分析，识别模型输出响应的重要影响参数，减少了模型参数率定过程中的盲目性，提高了模型运行的可靠性与预报精度［5］。

1 模型建立

首先，运用GIS对各流域数字高程模型DEM进行河网提取、子流域划分，提取各流域植被覆盖率、河床糙率与河床平均坡度等水文要素，再结合《山西省水文计算手册》中的汇流参数取值方法，对山西省洪水预报中的纳什瞬时单位线汇流模型参数进行初始设定，最后运用LH-OAT对流域汇流参数进行调试。通过分析调试前后模型输出的洪峰流量、洪水总量的变化，分析汇流模型参数的敏感性。

山西省洪水预报系统中的纳什瞬时单位线汇流模型共有5个汇流参数，除了参数C1、C2外，其他参数均有明确的经验值。根据LH-OAT敏感性分析法的基本原理，其他参数不满足抽样条件，不需要进行调试，其敏感性不做研究。因此，本文只针对汇流模型参数C1、C2进行敏感性研究。

2 研究方法

2.1 研究流域概况

分别选用山西省境内飞岭、固定桥、南庄3个水文站作为研究对象。飞岭水文站位于山西省安泽县府城镇飞岭村的沁河干流上，控制流域内有3处水位站，14处雨量站;固定桥水文站位于山西省大同县吉家庄乡固定桥村西桑干河畔，控制流域内有26处雨量站;南庄水文站位于山西省定襄县南庄村滹沱河畔，控制流域内有42个雨量站。上述3个流域的研究资料皆来自于多年连续记录的降雨量摘录表、洪水摘录表、日蒸发资料。分别选取3个水文站控制流域各5次场次洪水过程，利用标准面积洪峰流量对场次洪水进行等级划分并进行敏感性研究。各流域概况与洪水信息见表1。

由表1可知，所选场次洪水涵盖4个等级，一方面可对比分析不同等级洪水下的参数敏感度;另一方面3个流域的空间尺度、森林覆盖率、主河床平均糙率与河床平均纵坡各不相同，产生的参数有一定差异，可对比分析流域特性对汇流模型参数的影响。

2.2 LH-OAT敏感性分析法

LH-OAT算法是全局敏感性分析法的一种，该算法结合了抽样法(LH)的健壮性与敏感性方法(OAT)的精确性［6］。具体内容如下:①首先进行LH抽样，把每个参数的取值范围均匀分割为层，将每个参数按照先前分割的层级，一一对应进行参数随机抽样，每层每次抽一次，则有n个LH抽样参数组产生，每个参数组包含w个参数;②根据OAT思路，将每个LH抽样参数组中的1个参数进行微小改变，计算目标函数随每次微小改变的变化情况［7］;③由LH-OAT算法可知，模型共进行了n(w+1)次运算。多个目标函数下汇流模型的参数敏感性计算公式如下

表1 流域概况与洪水过程

式中，O为目标函数输出结果;Fi表示模型参数;Ii为参数Fi在1个LH抽样集合的相对敏感度;Δ为参数Fi的定向改变量;Ii为参数Fi的相对敏感度。

根据式(1)计算出的相对敏感度大小，可将参数的敏感性进行分类，分类标准详见表2。

表2 敏感性分类

以第i场洪水中的洪峰流量Qmi、洪量Wi、过程相对误差RE、洪量精度评定指标IVF、洪峰误差PE、模拟流量残差平方和RSS作为此次汇流模型参数敏感性分析的目标函数。计算公式如下

式中，Wi和Wi'为实测和模拟洪量，Qmi和Qmi'为实测和模拟洪峰流量。

2.3 变异系数法的应用

由上文叙述可知，汇流模型参数敏感性大小是相对的，不同目标函数下，其模拟结果是不同的。本文以各有效目标函数为评价指标，采用变异系数法，通过权重将多个指标合成1个指标来最终描述敏感性，即通过计算模型参数的综合敏感性系数来最终描述汇流参数的敏感性，具体计算过程如下:

设有n个评价指标，每个评价指标中有m个指标数值，则各项指标的标准差为

式中，δj为第j项评价指标的标准差。各项指标的变异系数为

式中，vj是第j项评价指标的变异系数。

各项指标在所有评价指标中所占的权重为

式中，wij为第 j项评价指标在所有指标中所占的权重。

3 参数敏感性分析与讨论

运用LH-OAT法，对纳什瞬时单位线汇流模型参数C1、C2分别在其取值范围内分成5层进行LH抽样，抽样结果见图1，图中所示为等比例缩放后的取值。C1为单一地类汇流参数，取值范围为1.00～1.357;C2为复合地类汇流参数，取值范围为0.580～2.950(在同一种地质、地貌条件下，C2值反映流域植被的好与差［8］);然后对2个参数运用改进的LHOAT方法分析计算，根据LH-OAT方法定义，每个流域每场次洪水连续计算5×(2+1)=15次，计算不同目标函数下各流域汇流参数的对应敏感度，计算结果见表3。

由表3可知，目标函数为 IVF、RE、RSS、Wi的敏感性均为0，视为无效目标函数，不做分析研究;目标函数PE和Qmi为有效目标函数。下面将从不同等级洪水、不同目标函数、不同流域特性3方面入手，讨论分析PE和Qmi对汇流参数敏感性的影响。

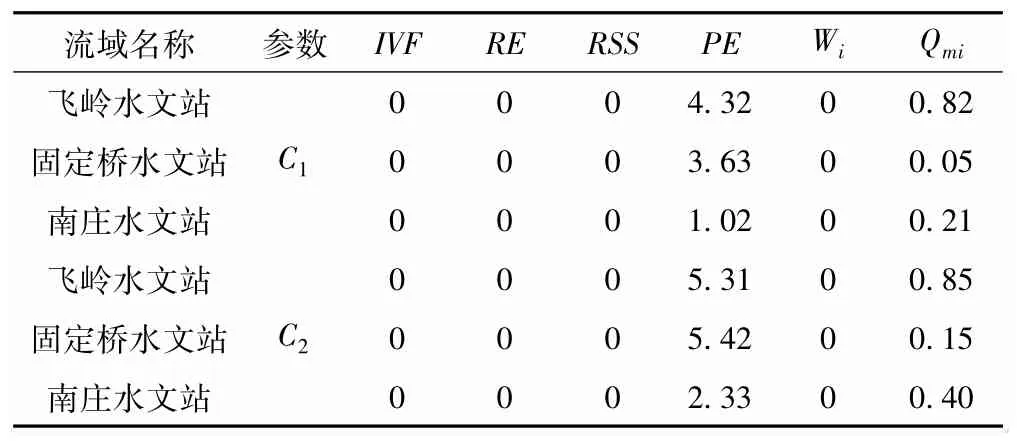
表3 不同流域汇流参数敏感性系数

3.1 不同等级洪水的影响

本文计算了飞岭、固定桥、南庄等3个水文站流域，共15场洪水的模型参数敏感度，并对比分析了3个流域在不同等级洪水下的敏感度变化情况。下面以南庄水文站控制流域为例，以PE、Qmi为目标函数，分析不同等级洪水参数敏感性变化情况。

南庄水文站流域不同等级洪水敏感性见图2。从图2可知，在不同等级洪水中，汇流参数C1、C2的敏感性等级基本上都随着洪水等级的增大而增大，这说明C1、C2均是对洪峰流量有重要影响的参数。在不同等级洪水中，各有效目标函数下，参数C2的敏感性变化特征均大于参数C1，这说明参数C2比参数C1对洪峰流量的影响更大，相关性也更强，是汇流模型中的重要参数。

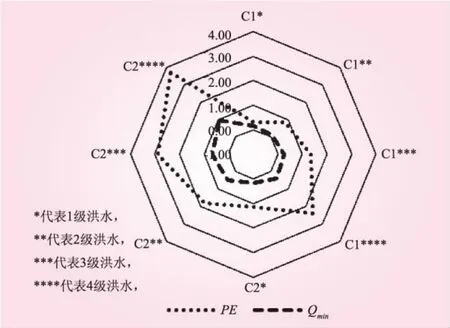
图2 南庄水文站流域不同等级洪水敏感性

3.2 不同流域的对比研究

对3个流域的汇流模型参数在相同目标函数下的敏感度情况进行对比分析，以目标函数PE、Qmi为例，分析纳什瞬时单位线汇流参数的敏感性变化情况。采用格拉布斯法(Grubbs)进行异常值分析，当定检水平p取0.01时无异常，置信概率大于99%，数据可靠。

横向来看，参数C1、C2在同一个流域内均能保持一致的敏感性等级;纵向来看，参数C1的敏感性等级会随着不同流域特性的变化而变化，敏感性不稳定，参数C2的敏感性波动性相对较小且敏感性等级较稳定，这也反映了不同流域特性的差异及汇流过程中存在的不确定因素对不同地类汇流参数敏感性的影响。

不同流域中，在敏感性等级相同的情况下，参数C2的敏感度总是要大于参数C1。

3.3 不同目标函数影响

从LH-OAT计算过程可以发现，汇流模型参数因模型计算结果的评价目标的不同而改变。

(1)各个汇流参数对于目标函数的敏感性整体上表现为C2＞C1。

(2)目标函数PE、Qmi均为有效目标函数。在目标函数PE中，参数C1、C2均达到了极敏感且C2的敏感性变化更明显。这体现出不同汇流地类参数对洪峰流量的影响，复合地类汇流参数对洪峰流量的影响更显著。

(3)对目标函数Qmi而言，随着洪水等级的不同、流域特性的差异，参数C1、C2呈现出了一般敏感性到敏感性的变化，不确定性和波动性更大。

3.4 汇流参数综合敏感性系数的确定

应用变异系数法并结合表3可得汇流模型参数综合敏感性系数，C1、C2综合敏感性系数分别为0.42、0.58。参数C1、C2均为敏感性参数，且C2＞C1。这基本与每个流域中每场次洪水中计算出的汇流参数的敏感性相一致，参数C1、C2均是影响洪水模拟精度的重要参数，符合山西省小流域洪水预报的实际情况。

4 结语

本文以山西省洪水预报系统中的纳什瞬时单位线汇流模型为研究对象，运用LH-OAT法对纳什瞬时单位线汇流模型参数进行抽样及敏感性分析，结合变异系数法确定在多目标函数下汇流模型参数的综合敏感性系数，得出以下结论:

(1)参数C1、C2是山西省洪水预报系统纳什瞬时单位线汇流模型中的重要影响参数，C2的综合敏感性系数大于C1，这与3个研究区域的敏感性分析结果一致。

(2)运用LH-OAT全局敏感性分析法对山西省洪水预报系统中的纳什瞬时单位线汇流模型参数进行敏感性分析，有效地提高了汇流模型参数的量化能力，确定了参数的重要程度，提高了模型模拟精度。

(3)纳什瞬时单位线汇流模型参数的敏感性受不同等级洪水、不同目标函数、不同流域特性的影响而发生改变。在实际汇流过程中，为达到更好的模拟效果，应深入了解纳什瞬时单位线汇流机理，结合不同地区的降雨径流资料及模型的实际运用，识别汇流模型重要的调节参数。

［1］孙颖娜．随机汇流模型及基于随机理论确定Nash模型参数的研究［D］．南京:河海大学，2006．

［2］周明，邓秋良．瞬时单位线汇流参数m1非线性改进方法探讨［J］．湖北水力发电，2006(1):9-11．

［3］何书会，杨慧英．小流域汇流参数分析［J］．海河水利，1997(5):15-16，48．

［4］金林．确定Nash模型参数方法的探讨［J］．水资源与水工程学报，2008，19(4):116-118．

［5］CIBIN R， SUDHEER K P， CHAUBEY I．Sensitivity and identifiability of stream flow generation parameters of the SWAT model［J］．Hydrological Processes，2010，24(9):1133-1148．

［6］MCKAY M D，BECKMAN R J，CONOVER W J．A comparison of three methods for selecting value of input variables in the analysis of output from a computer code［J］．Technometrics，1979，21(2):239-245．

［7］徐会军，陈洋波，李昼阳，等．基于LH-OAT分布式水文模型参数敏感性分析［J］．人民长江，2012，43(7):19-23．

［8］张泽宇，张永爱，梁存锋．流域水文模型在临界雨量分析中的应用研究［J］．人民黄河，2015，37(1):38-41．