一种基于TOPMODEL模型求解流域蓄水容量分布的方法

张 莹，李致家，缪成晨，孙如飞，姚 成

(1.河海大学水文水资源学院，江苏 南京 210098;2.扬州市水利局，江苏 扬州 225001;3.宁波市水利水电规划设计研究院，浙江 宁波 315192)

0 前言

概念性分布式模型自提出以来，其网格单元的蓄水容量求解问题始终是水文学者研究的热点和难点之一。传统的集总式水文模型从统计学角度提出了流域蓄水容量曲线的概念，在一定程度上解决了下垫面条件空间分布的不均匀性;但无法反映某个具体网格单元的蓄水容量与土壤类型、土壤特性和地形地貌之间的物理联系，使得流域蓄水容量曲线难以在分布式模型中广泛应用［1-2］。BEVEN和KIRKBY于1979年提出的TOPMODEL模型［3］为解决这一难题提供了思路，其中地形指数综合考虑流域地形地貌和土壤因素对流域径流形成的影响，饱和地下水面距地表深度与包气带厚度存在一定的物理联系。考虑到流域地形指数分布曲线与流域蓄水容量曲线所具有的相似性，石朋［4］等从统计学角度分析了网格单元蓄水容量与流域地形指数分布的定量关系，但忽略了蓄水容量与土壤、植被之间的内在联系的;向小华［5］等以VanGenuchten模型表述的土壤水分特征曲线为基础，推导出流域网格单元蓄水容量的计算方法，但其计算公式和相关参数求解复杂，在实际应用中具有一定的局限性。

考虑到目前求解网格单元蓄水容量方法的局限性，本文结合蓄水容量定义，分析TOPMODEL模型中饱和地下水面深D与网格单元蓄水容量WM的物理联系，构建了一种基于地形属性和土壤类型的网格单元蓄水容量的计算方法;并利用统计学方法推求出流域蓄水容量分布曲线，为概念性分布式水文模型参数的求解提供了参考。

1 网格单元蓄水容量计算方法构建

赵人俊教授在定义流域蓄水容量时认为，土壤中张力水是介于田间持水量和凋萎系数之间的含水量［6］;由此，可以得到计算流域内第i个网格单元蓄水容量WMi的计算公式

式中，WMi为第i个网格单元蓄水容量，mm;Hi为第i个网格单元包气带厚度，mm;θf，i为第i个网格单元田间持水量;θw，i为第i个网格单元凋萎系数。流域内每个网格单元的θf和θw可以根据对应网格单元的土壤类型确定［7］。由此可知，求解Hi是本研究的关键。

回顾包气带厚度H的定义，发现与TOPMODEL模型中饱和地下水面深D内涵一致，都是描述饱和地下水表面距离流域地表的深度，因此式(1)可以转化为

在TOPMODEL模型中，认为流域内某点饱和地下水面深Di由该点的地形指数来控制［8］，流域内某点饱和地下水面深

式中，Di为第i个网格单元饱和地下水面深，mm;D为流域平均饱和地下水面深，mm;Szm，i为第i个网格单元非饱和区最大蓄水容量，mm，即Szm，i=WMi;TIi为第i个网格单元地形指数;λ为地形指数均值。

地形指数也是TOPMODEL模型中提出的概念，第i个网格单元地形指数可由流域DEM数据计算得到，其具体的计算为

由式(3)和(4)代入式(2)可得第i个网格单元蓄水容量

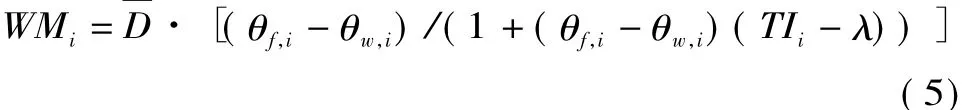
分析可知，求解第i个网格单元蓄水容量WMi，只需知道研究流域的平均饱和地下水面深D和地形指数分布情况，地形指数分布可以通过流域的DEM数据进行求解，关键在于如何求解D值。

相关研究表明，地形指数越大的网格，蓄水容量越小;地形指数越小的网格，蓄水容量越大［9］。假定流域内第K个网格单元地形指数最大，其值为TImin;则对应的蓄水容量最大值

将式(6)代入式(5)可得

式(7)为流域内网格单元蓄水容量求解公式。由式(7)可知，网格单元蓄水容量WMi由对应的土壤类型、地形指数TIi和流域单点最大蓄水容量WMmax控制。针对某个流域，只需给定流域单点最大蓄水容量WMmax，即可求出流域内蓄水容量的分布情况。

2 方法合理性验证

选取东湾流域为研究对象，其流域控制面积为2 789 km2，其多年平均降雨量为780 mm左右。东湾流域受人类活动影响较小，西部为山地森林地区，地形变化幅度较大，平均坡度较大;东部为丘陵灌木地区，地形变化幅度较小，平均坡度小。本次研究所利用的DEM数据是美国SRTM地形数据，土壤数据采自中国科学院土壤所公布的中国1∶100万的土壤数据库。东湾流域土壤类型主要为壤土、砂质粘土、粉砂土、粘土。利用公式(4)计算得到的东湾流域地形指数分布。

2.1 蓄水容量分布曲线特征分析

选取东湾流域2000年～2011年期间12场洪水过程对新安江模型进行参数率定，由模拟结果统计可得:径流深合格率为83.3%，洪峰合格率为83.3%，平均确定性系数为 0.85，依据 GB/T 22482—2008《水文情报预报规范》，洪水模拟结果达到乙级精度［10］，模型参数合理可靠，其中东湾流域的流域平均蓄水容量WM=180 mm，流域蓄水容量-面积分布曲线指数B=0.3。

为了保证两种曲线具有可比性，控制公式(7)中WMM值与新安江模型率定结果一致，即WMM=234 mm［5］，利用东湾流域的DEM数据和土壤类型数据，根据公式(7)计算流域内每个网格单元的蓄水容量值，得到流域蓄水容量-面积分布曲线，见图1。

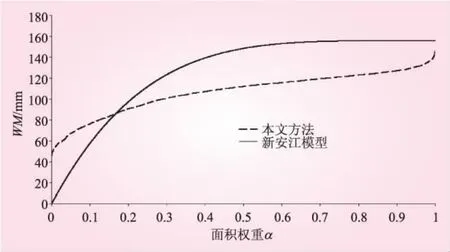
图1 流域蓄水容量-面积分布曲线

图1中两种曲线都呈抛物线，流域平均蓄水容量基本相同。但是，本文方法计算的流域蓄水容量-面积权重曲线较为平缓，蓄水容量空间分布差异较小，大多在100～200 mm之间，流域单点最小蓄水容量不为0，区别于新安江模型曲线。分析其原因为:①东湾流域地形变化幅度相对较小，土壤类型区域分布差异较小导致流域蓄水容量空间变化较小;②本文方法是以网格为计算单元，单点蓄水容量描述的是某个网格单元的平均情况，其值大小与网格单元内水面和坡面所占的比例有关，因此出现单点最小蓄水容量不为0的现象。

2.2 洪水模拟分析

利用本文方法计算得到的蓄水容量曲线对东湾流域2000年～2009年期间9场洪水进行参数率定，2010年～2011年的3场洪水进行参数验证，分别对径流深相对误差、洪峰相对误差和确定性系数进行统计，并与新安江模型进行比较，洪水模拟特征值统计见表1。两种方法的模拟结果比较:

(1)从均值角度看，新安江模型的径流深平均误差为12.7%，洪峰相对误差均值为10%，确定性系数均值为0.85;本文方法的径流深平均误差为11.8%，洪峰相对误差均值为11.1%，确定性系数均值为0.84。本文方法在径流深模拟方面优于新安江模型，洪峰模拟方面劣于新安江模型，两种方法整体模拟效果基本一致。

(2)从极值角度看，新安江模型径流深相对误差最大为26.53%，最小值为0.04%;洪峰相对误差最大值为36.52%，最小值为0.57%;确定性系数最大值为0.98，最小值为0.6。而本文方法径流深相对误差最大为28.35%，最小值为1.64%;洪峰相对误差最大值为33.7%，最小值为1.18%;确定性系数最大值为0.93，最小值为0.67。单从极值方面考虑，新安江模型略优于本文方法。

综上所述，本文方法计算得到的蓄水容量分布曲线在东湾流域洪水模拟中，应用效果良好。表明本文所提出的基于TOPMODEL模型的求解流域蓄水容量分布的方法是合理可靠的，可用于实际应用与研究。

3 结论与展望

本研究以蓄水容量的定义为出发点，探究流域蓄水容量分布求解方法，提出了基于TOPMODEL模型的流域蓄水容量分布计算方法，建立了网格单元蓄水容量与地形、土壤类型的定量关系，对概念性分布式水文模型参数的求解具有一定的参考意义。根据东湾流域的地形和土壤分布特征，分析本文方法与新安江模型蓄水容量-面积曲线存在差异的原因，并通过洪水模拟分析，验证了本文方法的合理性，为概念性分布式水文模型参数的离散化计算提供了新思路，增加了分布式水文模型发展的可能。但是，本方法并未考虑不同分辨率的DEM数据和土壤类型数据对流域蓄水容量分布的影响，需要后期进一步的深入探究。

［1］芮孝芳，黄国如．分布式水文模型的现状与未来［J］．水利水电科技进展，2004(2):55-58．

［2］董艳萍，袁晶瑄．流域水文模型的回顾与展望［J］．水力发电，2008，34(3):20-23．

［3］BEVEN K J， KIRKBY M J．A physically based variable contributing area model of basin Hydrology［J］．Hydro Science Bulletin，1979，24(1):43-69．

［4］石朋，芮孝芳，瞿思敏，等．一种通过地形指数计算流域蓄水容量的方法［J］．水科学进展，2008，19(2):264-267．

［5］向小华，宋琪峰，陈喜，等．融合地形和土壤特征的流域蓄水容量模型［J］．水科学进展，2013，24(5):651-657．

［6］赵人俊．流域水文模拟—新安江模型与陕北模型［M］．北京:水利电力出版社，1984．

［7］姚成．基于栅格的新安江(Grid-xinanjiang)模型研究［D］．南京:河海大学，2009．

［8］谢帆，李致家，姚成．TOPMODEL和新安江模型的应用比较［J］．水力发电，2007，33(10):14-18．

［9］邓慧平，李秀彬．地形指数的物理意义分析［J］．地理科学进展，2002，21(2):103-110．

［10］GB/T 22482—2008 水文情报预报规范［S］．