测压管路对抽蓄机组过渡过程测试结果的影响

唐拥军，邓 磊，周喜军，刘 锋

(国网新源控股有限公司技术中心，北京 100161)

0 引 言［1-2］

随着我国经济社会的快速发展和调结构转型升级，抽水蓄能电站在电力系统中，尤其是可再生能源开发利用中发挥着越来越重要的作用。现阶段我国抽水蓄能事业迎来了发展高峰期，目前已有大量的电站处于运行或在建状态，未来还有一大批即将建设的项目。抽水蓄能电站的安全运行对于保证大电网的稳定至关重要。由于抽水蓄能机组具有转速快，水头高的特点，因此，水力过渡过程尤其发电方向甩负荷成为抽水蓄能机组安全运行所关注的重点。新建机组在启动调试时会进行各种水力过渡过程的试验并进行相关测试，若压力测点位置选择不当或测压管路过长则可能造成测试结果不正确，从而对机组的水力过渡过程性能形成错误评价。本文以某抽水蓄能机组甩100%额定负荷过程为例，用经验模态分解方法(EMD)对甩负荷过程机组压力进行了分析，论证了上述观点的正确性。

1 机组基本参数

该抽蓄机组的基本参数如表1所示。该机组过渡过程参数蜗壳进口压力与转速上升率保证值中，蜗壳进口中心线处最大压力值不大于850 m水柱;所有过渡过程工况中机组产生的转速上升率不大于50%。

表1 机组基本参数统计表

2 经验模式分解EMD［3］

经验模式分解EMD(Empirical Mode Decomposition)，是一种自适应的信号分解方法，它把复杂信号分解为有限的基本模式分量IMF(Intrinsic Mode Function)及一个余项的和。

EMD方法是用波动上、下包络的平均值去确定“瞬时平衡位置”，进而分解出各IMF分量，考虑一个信号序列x(t)，经验模式分解过程如下:

(1)确定信号所有的局部极值点，然后用三次样条线将所有的局部极大值点连接起来形成上包络线，再用三次样条线将所有的局部极小值点连接起来形成下包络线，上、下包络线应该包络所有的数据点。上、下包络线的平均值记为m1，求出

理想地，如果h1是一个IMF，那么h1就是x(t)的第一个分量。

(2)如果h1不满足IMF的条件，把h1作为原始数据，重复步骤(1)，得到上下包络线的平均值m11，再判断h11=h1－m11是否满足IMF的条件，如果不满足，则重循环 k次，得到 h1(k－1)－m1k=h1k，使得h1k满足IMF的条件，记c1=h1k，则c1为信号x(t)的第一个满足IMF条件的分量。

(3)将c1从x(t)中分离出来，得

将r1作为原始数据重复步骤(1)、(2)，得到x(t)的第2个满足IMF条件的分量c2，重复循环n次，得到信号x(t)的n个满足IMF的分量。这样就有

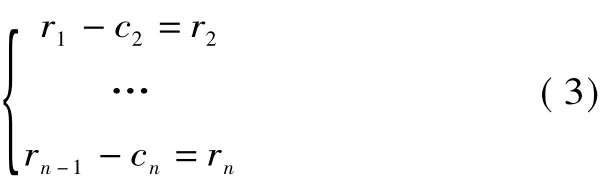
当rn成为一个单调函数不能再从中提取满足IMF的分量时，循环结束。这样由式(2)、(3)得到

因此，可以把任何一个信号x(t)分解为n个基本模式分量和一个残量rn之和，分量c1，c2，…，cn分别包含了信号从高到低不同频率段的成分，而且不是等带宽的。所以，经验模态分解是基于与不同时间尺度有关的能量的直接提取上进行的。

3 测试结果与分析［4］

该机组甩100%额定负荷过程，测量了机组的压力、转速和振动摆度等，本文就机组压力中的球阀后压力进行分析。球阀后压力进行了两个位置的测量，一处位于蜗壳层球阀后压力钢管上，另一处为用测压管路将球阀后压力引致水轮机层的水力测量表盘处，引压管路长度约为5 m，两测点的高程差为3 m。

该机组甩100%额定负荷过程，球阀后压力蜗壳层测点与水轮机层测点变化曲线见下图1，由图1可知，水轮机层测点的最大值为8.139 MPa，蜗壳层测点的最大值为7.656 MPa。尽管两测点的数值均满足合同保证值要求，不过，两者相差0.483 MPa(未考虑两测点高程差)，相差数值还是较大的。为分析两者之间的差异，采用经验模态分解EMD来进行分析，分析时段选取图1中5～15 s。

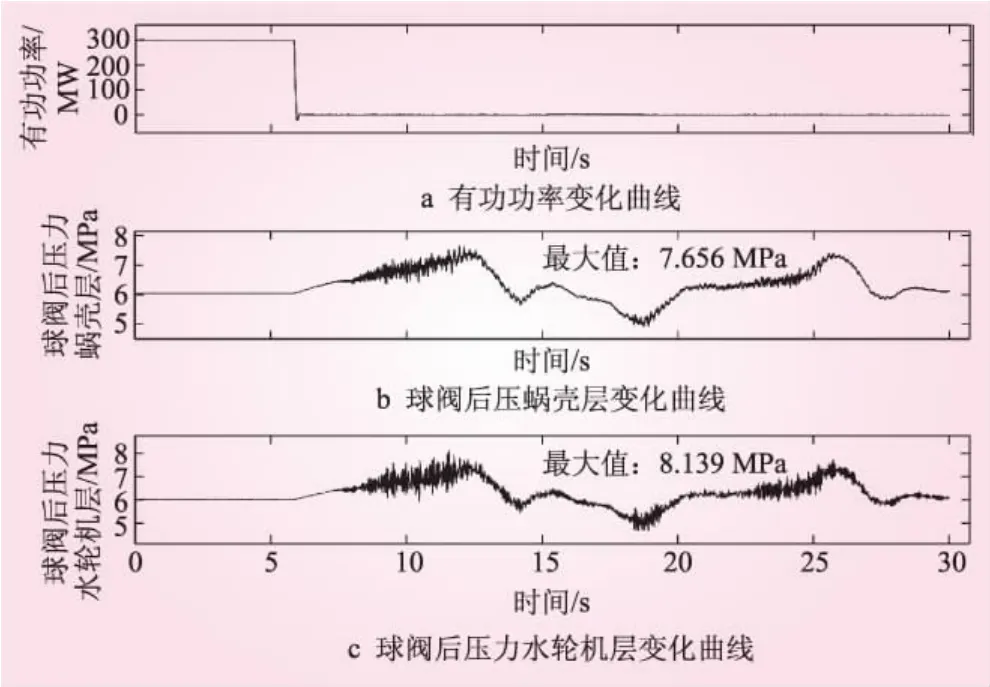
图1 甩300 MW负荷过程有功功率与球阀后压力时域变化曲线

先对球阀后压力水轮机层与蜗壳层测点进行EMD分解，两测点均分解得到9个IMF和1残量，然后对分解得到的各IMF和残量进行FFT变换，进而得到的频域幅值谱两测点前4个IMF的频域幅值谱如图2、3所示，由分析结果可知，球阀后压力蜗壳层测点中有430～500 Hz的高频成分，而水轮机层测点中没有;水轮机层测点中16～20 Hz的频率成分幅值较大，其中20 Hz左右频率成分双幅值达到了0.14 MPa，而蜗壳层测点中20 Hz左右频率成分的双幅值仅为0.01 MPa左右，两者相差约14倍。

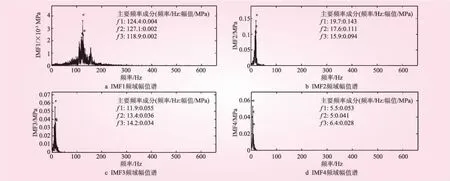
图2 球阀后压力水轮机层测点前4个IMF对应的频域幅值谱

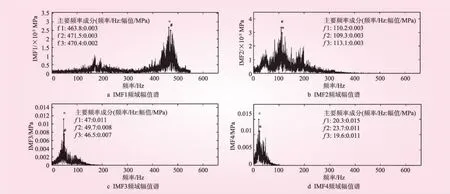
图3 球阀后压力蜗壳层测点前4个IMF对应的频域幅值谱

水轮机层测点EMD分解中的IMF2舍去，剩下的各IMF与残量重构得到球阀后压力水轮机层，蜗壳层测点EMD分解中的IMF1舍去，剩下的各IMF与残量重构得到球阀后压力蜗壳层，这两个重构信号的对比见图4。

由图4可知，两者的变化趋势基本一致，此外，球阀后压力蜗壳层最大值为7.649 MPa，球阀后压力水轮机层最大值为7.684 MPa，两者相差仅0.035 MPa，相比之前的0.483 MPa减小了0.448 MPa(约93%)。可见球阀后压力水轮机层测点中16～20 Hz的频率成分是由测压管路额外引入的。

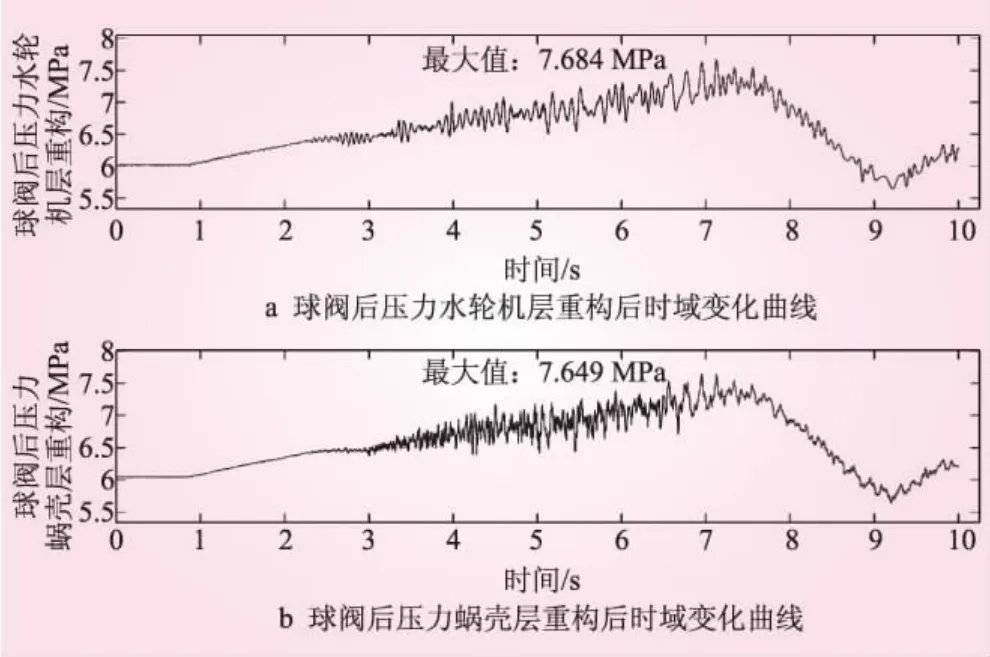
图4 球阀后压力水轮机层与蜗壳层重构信号对比曲线

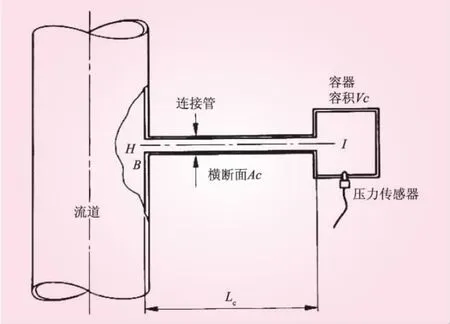
图5 有连接管时压力传感器安装示意

如果压力测量采用的结构如图5所示，则传感器在I处测得的信号与在II处测得的信号相比将发生偏差。当信号的频率达到第一临界频率fC时，这一偏差将特别显著。当壁面为刚性、系统中没有气泡时，并且忽略阻尼、假定为小振幅脉动及管路直径与aC/fC)相比很小，VCACLC时，第一临界频率fC的计算公式为

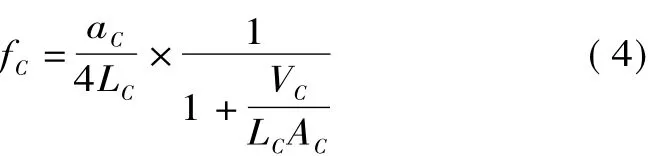
式中，aC为连接管中压力波的传播速度;LC为压力测量连接管长度;AC为压力测量连接管直径;VC为压力传感器安装处容器容积。

查阅相关文献可知，水压力波速为1 200 m/s左右，又测压管路长约为5 m，因此可计算得到第一临界频率fc的近似值为60 Hz，这与16～20 Hz相差较大，由此可知造成球阀后压力水轮机层测点压力偏大的原因不是第一临界频率，而很可能是与引压管路排气未尽或引压管路固定不牢固有关。

4 结语

(1)测量引压管路对压力脉动中的高频成分有明显的阻尼作用。

(2)测量引压管路可能会引入额外的频率成分，从而造成压力测量结果偏大，影响对机组过渡过程性能的正确评价。

(3)压力测点布置应尽可能接近被测量部位，测压管路应可能地短。建议主机厂家在设计时考虑测试用的测点开孔和测压管路布置。

(4)经验模态分解EMD具有自适应分解特性，非常适用于过渡过程等非平稳信号的分析。

［1］发改能源2014—2482号 国家发展改革委关于促进抽水蓄能电站健康有序发展有关问题的意见［S］．

［2］袁寿其，方玉建，袁建平，等．我国已建抽水蓄能电站机组振动问题综述［J］．水力发电学报，2015(11):1-15．

［3］崔玲丽，高立新，张建宇，等．基于EMD的复合故障诊断方法［J］．北京科技大学学报，2008(9):1055-1060．

［4］GB/T 17189—2007 水力机械(水轮机、蓄能泵和水泵水轮机)振动和脉动现场测试规程［S］．

［5］程军圣，于德介，杨宇．EMD方法在转子局部碰摩故障诊断中的应用［J］．振动、测试与诊断，2006(3):24-27．

［6］田锋社．水轮机压力脉动测试的分析与探讨［J］．水利水电科技进展，2006(4):37-40．

［7］叶复萌，朱渊岳，樊红刚，等．抽水蓄能电站复杂管系的自激振动研究［J］．水力发电学报，2007(8):135-140．

［8］周攀，周东岳，邓磊．基于EMD方法的水力测量信号分析［J］．水电与抽水蓄能，2016(2):39-43．

［9］陈喜阳，闫海桥，孙建平．基于EMD-FFT的水电机组振动信号检测［J］．水力发电，2014，40(5):51-54．

［10］游光华．天荒坪机组甩负荷试验压力钢管压力上升分析［J］．水电站机电技术，2002(2):76-78．

［11］李承军．抽水蓄能机组压力脉动的测试与分析［J］．水力发电，2001(5):53-55．

［12］邓磊，宋德强，周攀，等．抽水蓄能电站过渡过程蜗壳压力设计研究［J］．大电机技术，2016(5):42-47．