新拌自密实混凝土DEM接触模型开发及其数值实现
2017-03-20黄小龙宋慧芳
崔 溦,黄小龙,宋慧芳,李 明
(天津大学水利工程仿真与安全国家重点实验室,天津 300354)
0 引言
在密布钢筋和复杂模板形态下采用自密实混凝土(SCC)进行浇筑具有极大优势。现有设计中,由于室内试验真实再现实际复杂施工环境存在一定难度,采用数值模拟手段研究SCC浇筑施工就成为一个较好的选择[1]。基于连续介质力学的CFD(计算流体动力学)模拟和基于非连续介质力学的离散模型都可以用来对新拌混凝土进行模拟。在已有的模拟方法中,SCC经常被当作是一种均匀各向同性连续的物质,其力学行为在连续力学或者流体力学框架下进行研究[2]。但严格来讲,像混凝土这种由于组分颗粒粒径(从纳米尺度到厘米尺度)存在显著差异的各向异性材料,其与一般流体介质有较大区别,采用CFD模拟精度较差[3],同时,亦不能评价其通过能力和抗离析能力。依据离散建模的方法,可以把混凝土看作是各向异性的多相材料。因此,离散单元法(Discrete Element Method)很适合以细观角度研究 SCC 的宏观行为[2,4]。
离散元理论的核心是颗粒间的接触模型。对于SCC来说,粗骨料之间的接触作用与砂浆密切相关,同时,间距直接影响到骨料之间的摩擦、粘结作用,间距过大甚至会导致骨料连接断开,在现有的研究水平下,尚没有能完全契合这种接触关系的本构模型。考虑到工作量和计算精度,本文将SCC的3D离散元模型看作是粗骨料颗粒-砂浆-粗骨料颗粒的两相体系进行简化计算[5],其中砂浆的影响用液桥模型和hertz弹簧加以体现。
本文首先对自定义SCC的3D离散元接触模型进行理论研究,并使用PFC3D(Particle Flow Code in Three Dimension)平台进行开发,通过算例验证程序编制的正确性。根据真实级配生成粗骨料颗粒,利用自定义接触模型对L型箱试验进行数值模拟,分析新拌SCC的流动性和通过能力,对比数值模拟结果和试验结果验证自定义离散元接触模型的准确性和可行性。
1 离散元原理
在离散单元法中,颗粒之间的相互作用被认为是向整个材料颗粒内部合理平衡状态靠近的动态方程。离散元通过时步差分算法循环计算,对每个颗粒反复应用牛顿第二定律。对于每个接触反复运用接触关系,不断更新模型的单元位置和单元间的作用力,直到每一个颗粒都不出现不平衡力和不平衡力矩为止。每个单元的运动都可以通过平移和旋转运动相关的合力和合弯矩的方程组表示。把每个单元都当成球体,得到单元质量mi,位置矢量γi,惯性矩Ii,控制方程如下

2 接触模型的开发
2.1 自密实混凝土离散元模型的建立
目前,按SCC组分简化方式不同,主要数值模拟方法可分为单向流体、颗粒流、悬浮液三类。本文采用真实级配的球形颗粒来描述粗骨料,物料中其他组分被当作是存在于粗骨料之间的流动砂浆。假定将砂浆看成是连续、各向同性的均一流体,其在数值模拟时通过影响粗骨料间的相关力学模型参数,直接作用在粗骨料上。最终,本文将SCC离散成密相颗粒—填隙流体的两相介质。
在离散单元中增加液体的考虑时,颗粒间必然会产生复杂的粘附作用,然而目前还没有针对浆液与颗粒间相互作用的理论模型。本文参考近似非饱和状态下的液桥模型来描述有液体存在时粗骨料之间的力学行为,同时考虑骨料与骨料受压时,法向上采用非线性元件Hertz弹簧[6]描述力与位移之间的关系,而切向采用库伦摩擦准则。
2.2 模型理论
自定义模型SCContact(见图1)提供了一个无限小的非线性摩擦平面,接触平面有表面接触力Fs和液桥力Fm两种作用力。其中,表面作用力Fs包括Hertz力Fh和阻尼力Fd,两者的力学元件相互平行,分别表示为由于Hertz弹簧不能承受拉力因此接触面的力矩Mc≡0,摩擦片通过摩擦系数μ与法向力关联并产生切向力,遵循库伦极限准则。同时,在颗粒的法向上引入液桥力Fm[7]。

图1 自定义模型-SCContact
2.3 力与位移关系定律
接触力总和为

式中,Fm为液桥力;Fs为表面作用力由Hertz力和阻尼力组成

表面接触力 Fs可以分解为法向力Fs,即和切向力



2.4 力的更新
力和位移准则在自定义模型中的更新分为以下三步:
(1)当Fm≤0时,按照如下公式对Fm进行更新

式中,gc为颗粒间距;scr为颗粒临界间距,scr=2R0=(R1+R2)R0,其中,R1,R2分别为两球半径,R0为平均半径;Fm,max为最大液桥力,其中,τeq为等效表面张力系数。
(2)法向表面力更新准则

(3)切向力更新推导如下:

Hertz切向力
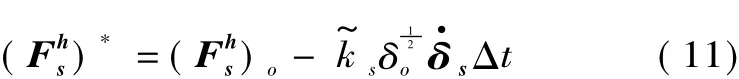


切向力更新
2.5 模型的数值实现流程
PFC自定义模型根据以上给出的位移增量,得到新的接触力,模型文件的编写主要包括:基本类的描述、成员函数的描述、模型注册、模型与PFC之间的信息交换,通过C++面向对象的语言编写而成,根据模型的微观设计理论编写模型,以动态链接文件的形式进行存储,将文件放在PFC的指定安装目录中,在计算过程中通过加载命令,主程序会自动调用用户指定的接触模型。自定义接触模型的整个使用方法如图2所示。
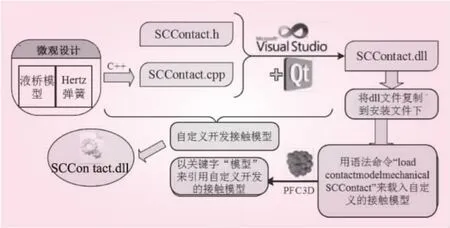
3 算例验证
自定义模型在调试成功后,为了验证该模型中接触力随位移的变化情况,通过两个颗粒之间的相互作用验证自定义模型的正确性。模型所采用的相关力学参数见表1。模拟使用半径分别为5 mm和7.5 mm的两个小球,分两种情况进行:①颗粒之间受压模拟Hertz弹簧,过程为蓝色颗粒固定,绿色颗粒沿y轴负方向运动0.001 m停止,如图3a所示;②颗粒之间受拉模拟液桥模型,过程为从两颗粒相互接触开始,蓝色颗粒固定,绿色颗粒以较小的速度沿着y轴正向运动,直至颗粒间距离大于临界距离0.012 5 m。颗粒间的液桥断裂,接触消失,如图3b所示。

表1 接触模型的力学参数
4 实例分析
L型箱是测试评价SCC工作性能的常见仪器之一,能够很好地模拟新制SCC的半静态浇筑条件,通过测试拌和物从竖向柱内通过钢筋间隙后流向水平槽的能力,反映了SCC拌和物的流动性和间隙通过性[8]。
4.1 试验用混凝土材料性质及配比

图3 程序计算结果与理论计算结果对比
各国关于SCC配合比共同点是:强调粗骨料的体积分数。粗骨料对SCC拌和物的自密实性能起着与浆体一样的关键作用。参照 EFNARC[9]推荐的SCC配合比参数范围和配合比设计方法,采用的混凝土配合比如表2所示。粗骨料宜采用连续级配或者2个及以上单粒径级配搭配使用[8],对于复杂结构工程不宜大于20 mm,具体级配见表3。

表2 自密实混凝土配比

表3 粗骨料颗粒分布
4.2 试验方法
测试时,将L型箱放在水平面上,用水润湿模具内部,在仪器垂直部分装满混凝土试样,将SCC静置1 min后再提起闸板,同时记录SCC流经各刻度标注点的时间以及最终时刻的流动形态。为了进一步验证开发接触模型的科学性,对SCC的L型箱试验进行DEM模拟。数值模拟的球体粒径级配按照表3生成。每个粒径组的粒径分布符合正态分布。
4.3 结果分析
室内试验确定该SCC的坍落度为617 mm,以此结果为基础,确定主要细观参数取值如表4所示。

表4 接触模型的力学参数
试验结果表明,混凝土流动到距离闸板200 mm时,试验值为2.0 s,模拟值为1.6 s;混凝土流动到距离闸板400 mm时,试验值为5.1 s,模拟值为4.8 s;混凝土流动到距离闸板600 mm时,试验值为11.2 s,模拟值为10.8 s。流动状态对比见图4,流动停止时表面形态对比见图5。

图4 流动状态对比

图5 流动停止时表面形态对比
从图4可以看出,流动到相同位置时,数值模拟的时间均短于相应的试验值,这是因为数值模拟时闸板瞬间打开,而在室内试验时,闸板开启时有一定的时间延迟,但结果相差不大,平均误差为4%。从图5可以看出,流动停止时模拟和试验的流动液面状态有一定差别,主要是由于以圆球代替不规则的粗骨料,比真实的SCC颗粒间的空隙更大,但总体吻合较好。试验值H2/H1=0.84≥0.8,模拟值H2/H1=0.83≥0.8,因此配制的SCC具有良好的间隙通过能力。从上述分析可知,基于DEM开发的3D接触模型对SCC工作性能的模拟能对模板内混凝土的流动时间和流动形态进行预测分析,可以为工程实践提供参考。
5 结论
(1)考虑粗骨料间距离影响,结合液桥理论和Hertz弹簧开发了新拌SCC离散元接触模型,该模型较好地揭示了粗骨料—砂浆—粗骨料之间的粘结、摩擦、断开等相互作用,且细观参数较少,也更易确定。
(2)采用面向对象的编程技术开发了新拌SCC离散元接触模型子程序,并通过算例进行验证,结果表明理论解和数值解基本一致。
(3)对SCC在L型箱内的流动时间和流动形态的试验值和模拟值进行了对比分析,结果表明:流动时间的模拟和试验值平均误差为4%,结果接近;SCC最终流动形态的模拟值和试验值吻合较好,描述其通过能力的关键指标也基本一致,表明建立的离散元接触模型能够较精准地模拟SCC的工作性能。
[1]OKAMURA H,OUCHI M.Self-compacting high performance concrete[J].Progress in Structural Engineering & Materials,1998,1(4):378-383.
[2]ROUSSEL N,GEIKER M R,DUFOUR F.Computational modeling of concrete flow:General overview[J].Cement& Concrete Research,2007,37(9):1298-1307.
[3]HOOMAHAD H,KOENDERS E A B,van BREUGEL K.Toward the development of self-compacting no-Slump concrete mixtures[J].Epitoanyag-Journal of Silicate Based and Composite Materials,2015,67(4):135-138.
[4]MECHTCHERINE V,GRAM A,KRENZER K,et al.Simulation of fresh concrete flow usingdiscrete element method(DEM)[J].Materials& Structures,2014,47(4):615-630.
[5]HOORNAHAD H,KOENDERS E A B.Simulating macroscopic behavior of self-compacting mixtures with DEM[J].Cement& Concrete Composites,2014,54:80-88.
[6]MINDLIN R D,DERESIEWICZ H.Elastic spheres in contact under varying oblique forces[J].Journal of Applied Mechanics 1953,20(3):327-344.
[7]LIAN G, THORNTON C, ADAMS M J.A theoretical study of the liquid bridge forces between two rigid spherical bodies[J].Journal of Colloid & Interface Science,1993,161(1):138-147.
[8]JGJ/T283—2012自密实混凝土应用技术规程[S].
[9]HIRT C W,NICHOLS B D.Volume of fluid(VOF)method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39(1):201-225.
