关于初中生锐角三角函数概念理解水平的调查分析
2017-03-20孙牟昕景敏
孙牟昕+景敏
[摘 要] 在数学课程标准和各版本教材中没有将锐角三角函数分列到函数领域,但是锐角三角函数的名称和数学本质都明确地体现出函数的味道。通过问卷的方式,对九年级学生对锐角三角函数概念的理解情况进行调查,并分析部分学生不理解锐角三角函数中的自变量和因变量以及对应关系,不能区分锐角三角函数与已学函数之间异同。
[关键词] 锐角三角函数;调查研究
在日常教学中,初中数学教师普遍反映初中学生学习锐角三角函数比较困难,特别是对于三角函数概念的理解更显得困难。同时初中数学教师也反映学生对锐角三角函数理解存在很多问题。为全面了解初中生学习锐角三角函数时的困难,以及困难产生的原因,我们进行了本次抽样调查。同时也希望通过本次调查,能够寻找和确定合理教学要求,适度调整教与学方式方法,从而使学生高水平地理解三角函数概念。
一、关于锐角三角函数的认识
在相似的直角三角形中,当锐角大小确定以后,直角三角形中某两边的比值就随之确定,且有唯一比值与之对应。这就是说,针对每一个锐角,都有唯一一个数值与它对应。基于初中阶段的函数定义:“设在一个变化过程中有两个变量X与Y,如果对于X的每一个值,Y都有唯一的值与它对应,那么就说X是自变量,Y是X的函数”,锐角三角函数符合初中阶段函数定义。但与一次函数、反比例函数和二次函数相比,锐角三角函数是一类特殊的函数。其特殊性主要体现在对应关系及其表示方式上。例如,一次函数对應关系中,函数值是通过对自变量的代数运算得到的,并且这种对应关系直接借助于该运算表达式进行表示。而锐角三角函数的函数值不是通过对自变量(角度)的代数运算表达式来表示,而是依托于直角三角形,通过确定与该角具有某种位置关系的某两边的比值得到的,并且使用比较抽象的符号表示某两个边的比值,且不同两边比值采用不同符号。
二、研究方法
(一)样本
调查样本选自三所学校,其中两所学校是辽宁省课程改革示范校,共从中随机选取九年级四个班的147名学生;另一所学校是鞍山市城乡结合部某普通初中,从中随机选取九年级一个班级的29名学生。由于这三所学校都采取了阳光分班,因此,这样选择调查样本保障了样本的代表性。
此外,调查的时间选择在学生均已学习过一次函数、二次函数、反比例函数和锐角三角函数。
(二)调查工具
根据调查目的——调查学生对锐角三角函数概念的理解水平,将问卷分为以下三个方面:学生对函数基本概念的理解,对锐角三角函数概念的理解和锐角三角函数与其他函数的差异。为了考查学生对函数概念的理解情况,我们要求学生写出函数的概念。为了考查学生对锐角三角函数本质的理解,问卷中设计了三个题目。一个是“你认为锐角三角函数的本质体现了什么”并给出三个选项,意在考查学生在有错误选项的干扰下能否选出锐角三角函数的本质描述。第二个题目是“只要角的大小确定了,那么这个角的三角函数值的大小也就确定了,请问你同意这种说法吗?并写出理由”,意在考查学生在特定情境下能否准确表述出锐角三角函数的本质。第三个题目是关于表达式中自变量与因变量的区分,目的为了考查学生在三角函数正弦表达式中能否准确运用函数的概念区分出自变量与因变量。此外,问卷中第四题让学生叙述锐角三角函数与其他函数的不同,意在调查学生对已学知识的整理程度。在问卷题目的设计与修改过程中,我们对特级教师和数学教育研究者进行了访谈,寻求建议,经过反复修改最终确定了问卷的有效性。
三、调查结果
本次调查回收问卷176份,有效问卷161份,整理后得到以下数据。
(一)学生对函数概念的理解水平
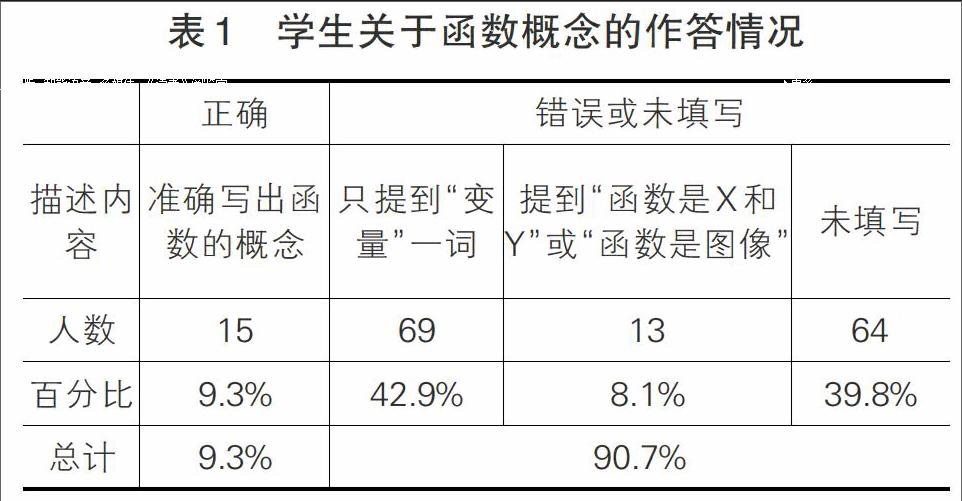
试卷中第三题是对学生函数概念理解水平的考查,要求学生写出函数的概念,学生的答案基本分为四类,如表1所示:
9.3%的学生能正确书写出函数的概念“设在一个变化过程中,有两个变量X与Y,如果对于X的每一个值,Y都有唯一的值与它对应,那么就说X是自变量,Y是X的函数”。有42.9%名学生的答案中提到“变量”这一词,例如,有学生写到“函数就是两个变量之间的关系”或“函数是变量X与变量Y的变化过程” 。但没有进一步说明对应关系指的是什么,等等。可见,学生对函数概念理解的准确程度很低。还有一部分学生,虽然知道函数概念,但在表述上不准确不完整。
(二)学生对锐角三角函数本质的理解
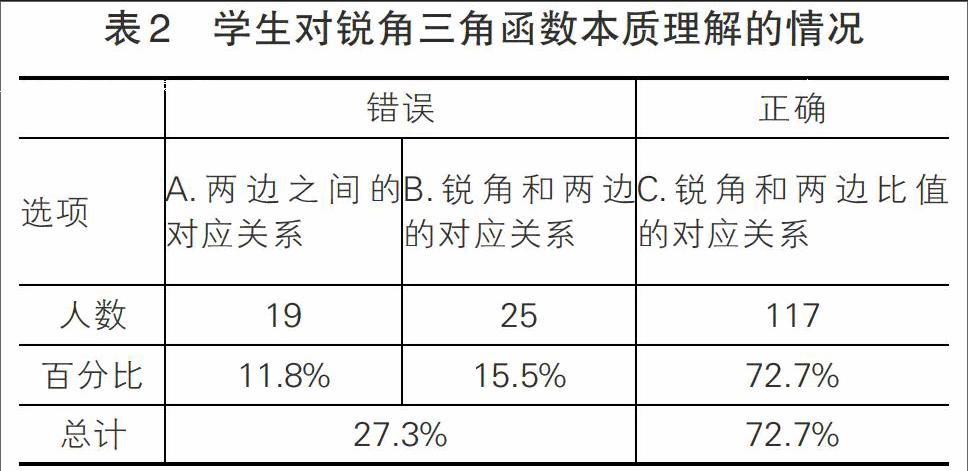
试卷中第二题、第五题和第六题考查了学生对锐角三角函数本质的理解。第二题设计为“你认为锐角三角函数的本质体现了什么?”,并给出表2中的三个选项,其中C为正确答案。数据如表2所示:
从上题可以看出,学生正确选出锐角三角函数的概念的人数比较多。但仍旧有27.3%的学生不理解锐角三角函数的概念,分不清锐角三角函数中是哪两个变量之间的对应关系。
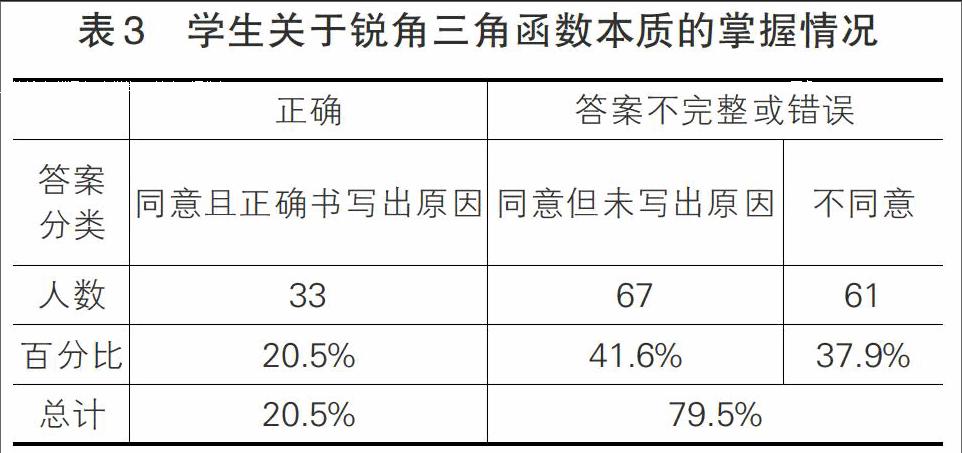
第五题是考查学生对锐角三角函数本质理解的判断题,题目设计为“只要角的大小确定了,那么这个角的三角函数值的大小也就确定了,请问你同意这种说法吗?并写出理由”正确答案应是同意该说法。数据如表3所示:
从表3我们可以看出,学生对锐角三角函数本质的理解水平较低,只有20.5%的学生正确判断并写出自己的理由。例如,回答正确的学生提到“因为三角函数值是直角三角形中一个锐角的对边和邻边的比,跟三角形的大小无关”或“大小不同的三角形是相似三角形,所以对应边成比例,只要角一定,边长比就一定”。无法表述原因或完全错误的学生占了大多数(79.5%)。
卷中第六题设计为关于表达式中自变量与因变量的区分,数据如表4所示:
本题为问答题,正确答案为∠A是自变量,是因变量。从问卷上可以看出还是有16.8%的学生能够区分自变量与因变量的,说明这些学生理解锐角三角函数中函数变量的对应关系。而其余学生(83.2%)将边长或∠A的正弦值当作变量的情况值得我们注意。
(三)关于学生对锐角三角函数与其他函数的区分
问卷中第四题考察了学生是否能准确区分锐角三角函数与其他函数的不同,请学生写出关于锐角三角函数与其他函数的区别,数据如表5所示:
本题为问答题,请学生写出锐角三角函数与一次函数、反比例函数和二次函数的区别。学生的答案可分为三类:“表达式不同”、“锐角三角函数是在固定的图形中解决问题”、完全错误。数据显示,学生在学习初中阶段涉及到的各种类型函数后,对知识间的联系程度较低,其表现是74.5%的学生说不出各个函数间的相同与不同之处。
四、讨论
通过问卷调查,本次研究得到的结论是,学生对函数概念的理解水平较低,部分学生不理解锐角三角函数本质,大部分学生不能找出各个函数之间的不同之处。下面我们将从三个方面来分析学生产生问题的原因。
从锐角三角函数的表达式方面来看,由于给三种锐角三角函数赋予了特定的符号(sin、cos、tan)。这三個符号在一定程度上没能够直观地给学生所谓的解析式的印象,隐去了函数与自变量之间的关系,即不能像一次函数那样直接呈现函数与自变量的关系,使得学生理解锐角三角函数中的函数与自变量的关系变得困难。
从教材编排看,部分教材将《锐角三角函数》这节课放在一次函数、反比例函数甚至是二次函数之后出现,因此,一次函数、二次函数、反比例函数的学习对三角函数学习产生负迁移,即导致学生误认为函数总是可以用X的解析式来表达的思维定式,从而影响了学生对锐角三角函数的理解。这种思维定式直接导致部分学生分不清锐角三角函数中的自变量和因变量,使得学生对锐角三角函数本质的理解出现困难。
从教师授课方面来看,教师没有从函数概念的高度引导学生理解锐角三角函数,没有说明锐角三角函数是明显地存在“对应”关系的函数,更多的是关注特殊角度所对应的两边比值。这样可能会导致一部分学生无法理解锐角三角函数的本质及与其他函数之间的不同之处。同时,大部分教师在讲授函数部分知识的时候,重视习题练习要多于给学生传授函数思想的应用,这样会弱化学生在函数概念和函数思想上的认识。
[参 考 文 献]
[1]石瑛.九年级学生对锐角三角函数的认知[D].华东师范大学,2009.
[2]濮安山.初中生函数概念发展研究[D].东北师范大学,2011.
(责任编辑:张华伟)
