基于因子分析的我国31个主要城市大气评估

陈 威

(华北科技学院,北京 东燕郊 065201)

0 引言

主成分分析[1-3]也被叫做主分量分析,其主要目的是从原始的多个变量中选取若干个线性组合,最大程度地保留原始变量中的信息。在运用统计学原理研究多变量的问题时,变量数太多则会大大增加计算量以及增加分析问题的复杂性,人们往往希望在进行数据分析时,研究较少的变量,得到较多的信息量。

本文通过运用主成分分析方法,对我国主要城市空气环境污染状况进行了总体比较和评价。数据研究表明, 哈尔滨、重庆、北京、石家庄、西安、太原等地大气环境污染比较严重; 大气环境质量比较理想的地区是海口、拉萨、南昌、长沙、广州、杭州等地。

1 主成分分析的原理和步骤

主成分分析主要是利用降维的思想，其主要原理是将多个互相之间有关联的数值变量转化成少数几个可解释总体数据但相互关联不大的综合指标的统计方法。这些综合指标就是原来多个变量的主成分，每个主成分都由初始变量的线性组合而成，而且各个主成分之间的相关性很小[4-6]。

利用主成分分析问题的主要计算步骤是：首先对原有变量进行标准化，然后计算各个变量之间的相关矩阵以及该矩阵的特征根和特征向量，最后将特征根由大到小排列，分别计算出对应的主成分。

主成份分析的主要目的是从原始多个变量中选取若干个线性组合,最大程度地保留原始变量中的信息,从原始变量到新变量是一个正交变换。设有X=(X1,X2,...,X3,XP) ,是一个p维随机变量,有二阶矩阵,考虑它的线性变换

(1)

从中容易得出如果要用Y1尽可能多地保留原始的X的信息,通常的方法是使Y1的方差尽可能大。其他Yi(i=1,...,P)也希望最大程度地保留X的信息,但前面的Y已保留的信息就不能再保留。一般的以累计贡献率达到85%为标准,对于一些特殊的问题也可适当的放宽只70%。它表示选定的主成分基本保留了原来变量的大部分信息[7-8]。在SPSS中主成分分析经常被嵌入到因子分析过程之中。

2 主成分分析法与环境污染指标降维

2.1 原始数据

表1数据来源于2016年中国统计年鉴，31个主要城市在2015年气体污染物物排放量,其中共有六个检测指标,包括: 工业二氧化硫 (X 1) ; 工业氮氧化物( X 2) ; 工业烟尘( X 3) ;生活二氧化硫( X 4) ; 生活氮氧化物( X 5) ;生活烟尘( X 6) 。

表1 各地区主要污染物排放情况

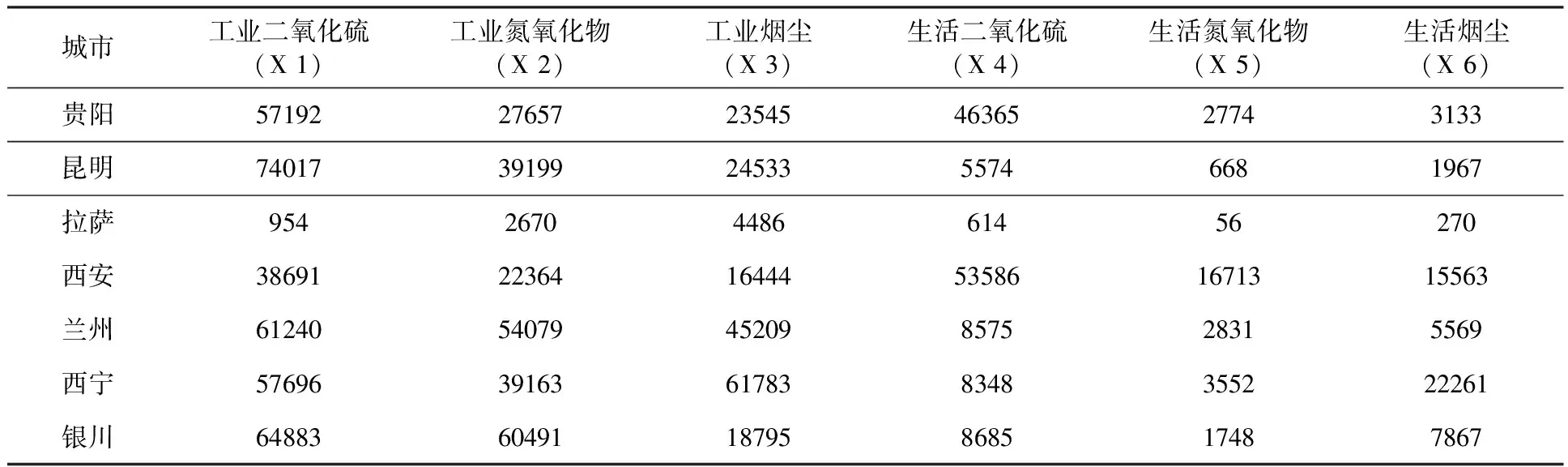
续表

2.2 数据分析

利用SPSS软件对原始数据作做主成分分析计算,在计算结果中提取了样本中协方差矩阵里两个大于1的特征值,其对方差的贡献率分别是51.255%和34.158% ,总贡献率高达85.413% ,超过85% ,主成分分析法适用于此类问的分析。

2.3 分析结果

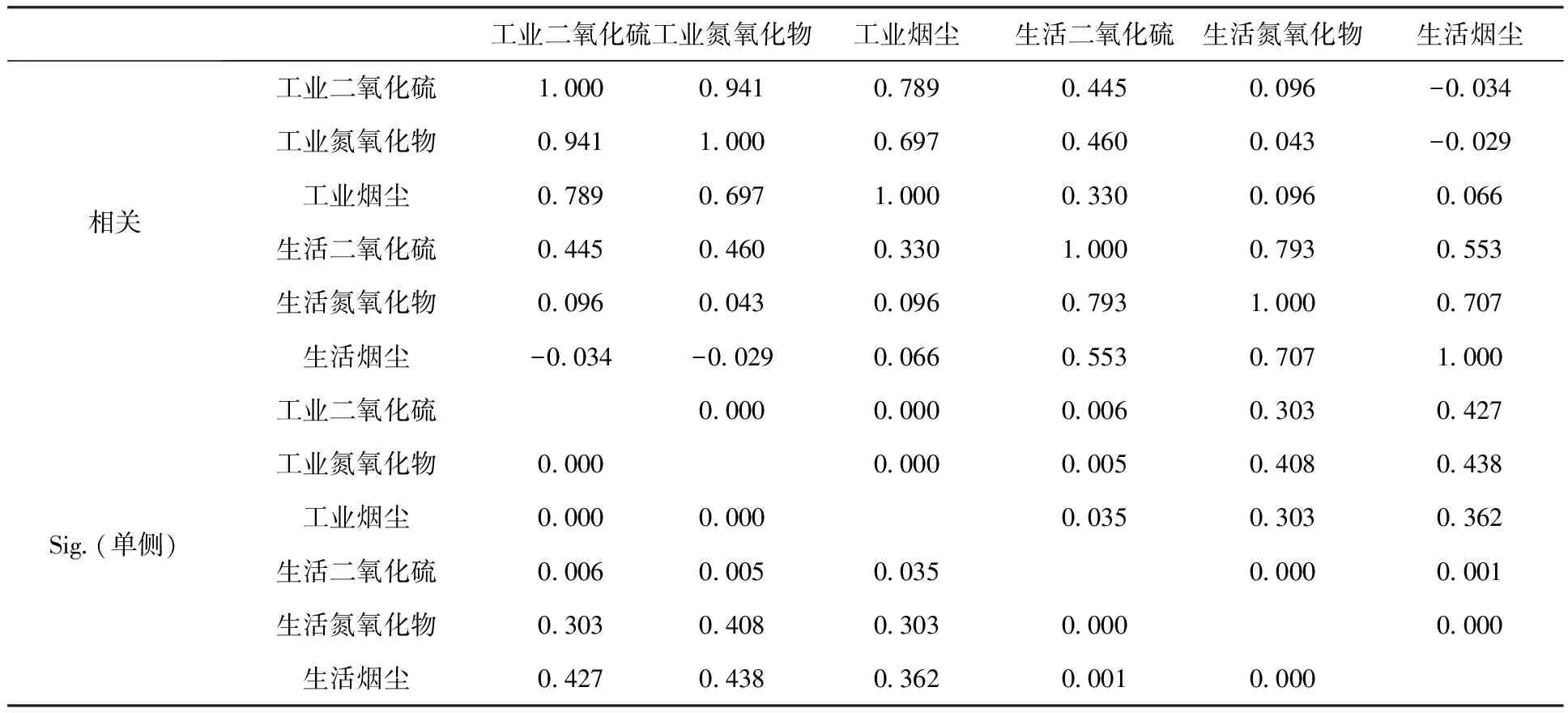
表2 污染物相关矩阵

由下表3球形检验可以看出KMO值为0.602，数据可以做主成份分析。显著性sig值为0.0001，该值比0.05小，线性相关强，并且小于0.01，说明差异性极其显著。综合考虑KMO与 Bartlett 检验，说明该数据相关性很强，适合做主成分分析。

表3 球型检验

根据表4和表5，我们可以看到6个主成分的特征值，方差贡献率以及累计方差贡献率，因为在标准值大于1时，累计贡献率达到85.413%，已经大于85%，同时根据碎石图(见图1)在第二个点位置出现拐点，第三个点位置之后折线趋于平缓，所以综合考虑选用2个主成分代替本来的6个指标，大大简化原数据信息。通过表6污染物排放的成分矩阵，得出成分矩阵最重要的两个主成分的关系式：

F1=0.856X1+0.828X2+0.767X3+0.796X4+0.530X5+0.392X6

(2)

F2=-0.473X1-0.470X2-0.397X3+0.473X4+0.784X5+0.781X6

(3)

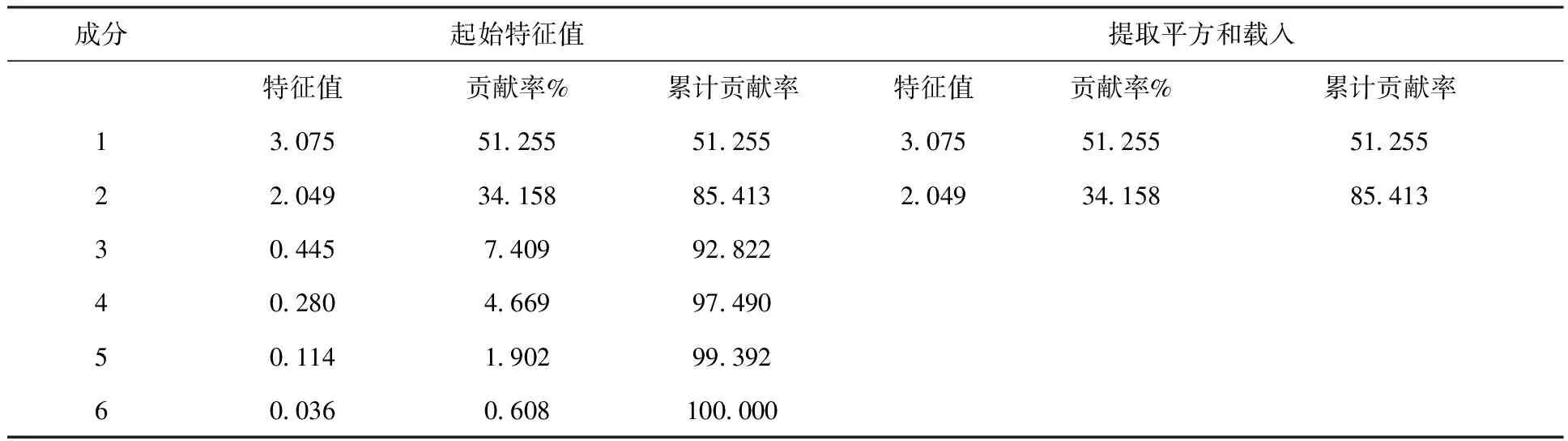
成分起始特征值提取平方和载入特征值贡献率%累计贡献率特征值贡献率%累计贡献率13 07551 25551 2553 07551 25551 25522 04934 15885 4132 04934 15885 41330 4457 40992 82240 2804 66997 49050 1141 90299 39260 0360 608100 000

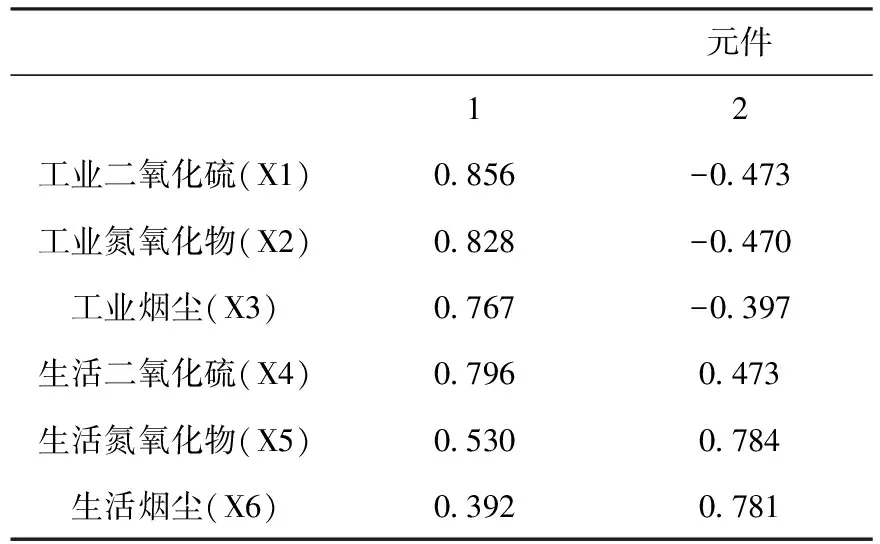
表6 污染物排放成分矩阵

在表6污染物排放成分矩阵中不难看出，与第一主成分密切相关的是工业二氧化硫、工业氮氧化物、工业烟尘以及生活二氧化硫，他们与第一主成分的相关性绝对值都超过75%，其贡献率达到51.3%，说明工业废气和生活二氧化硫对空气环境的影响较大。再看与第二主成分相关的是生活氮氧化物和生活烟尘，说明人类的生活多空气环境的影响也是较大的。通过对主成分因子一得分排序可知工业污染对空气影响较为严重的城市有重庆、上海、天津等城市，对主成分因子二得分排序可知生活污染对空气影响较为严重的城市有哈尔滨、北京、西安、石家庄等，通过加权得分公式：

F=(0.513F1+0.342F2)/0.855

(4)

式中，F为加权得分;F1为主成分因子一得分;F2为主成分因子二得分。

表7 各城市主因子一、二和加权得分降序表

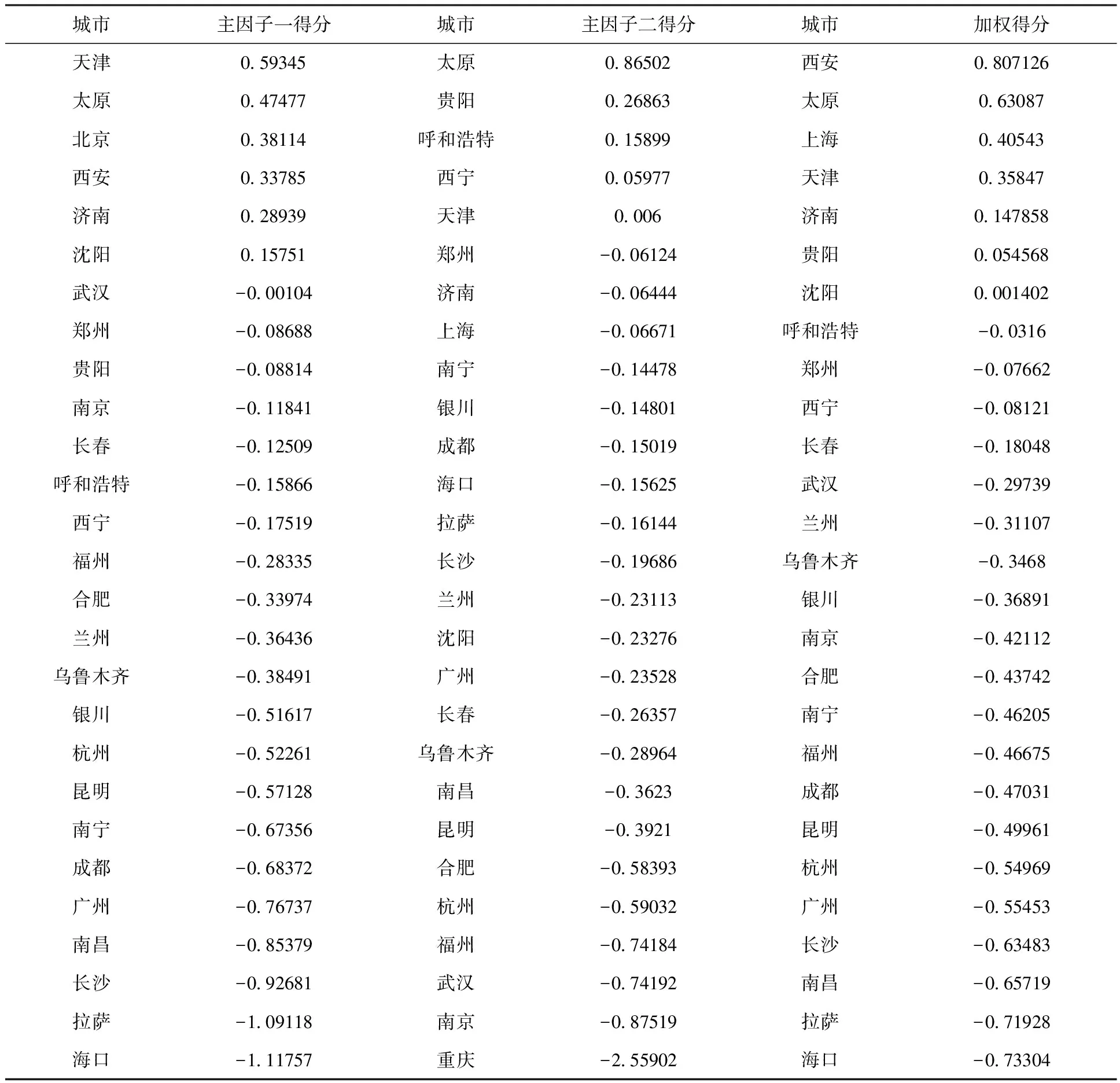
续表

得出各个主要城市的因子得分情况。根据表7可知重庆、上海、天津等城市工业污染对空气环境的影响较大，而哈尔滨、北京、西安、石家庄等城市生活污染对空气环境影响比较大。综合考虑两种主成分可知空气污染排在前几位的是: 哈尔滨、重庆、北京、石家庄、西安、太原等，空气质量较为理想的地区是海口、拉萨、南昌、长沙、广州、杭州等地。

3 结论

城市空气污染源于很多因素，各因素之间也有或多或少的联系。而运用主成分分析法来综合评价空气污染可以在较小损失的情况下得出影响空气质量的主要因素。根据上述方法对31个主要城市的空气质量统计综合分析得出重庆、上海、天津等城市工业污染对空气环境的影响较大，而哈尔滨、北京、西安、石家庄等城市生活污染对空气环境影响比较大。综合考虑两个主因素得知：哈尔滨、重庆、北京、石家庄、西安、太原等城市的空气污染严重，以工业污染废气污染为主。近几年，对于空气污染问题，我国提出了诸多相关的政策，对工业污染整治情况较为良好，同时也建议上述地区有关部门能够积极响应国家政策，对有关工厂加大治理力度，创造更加美好的生活环境。

[1] 王静龙. 实用多元分析[M].北京: 科学出版杜，2011：205-214.

[2] 李连香，许迪，程先军，等. 基于分层构权主成分分析的皖北地下水水质评价研究[J].资源科学，2015，37(1)：61-67.

[3] 李莉，孙永霞. 基于均值化主成分分析的雾霾环境分析与研究[J].计算机应用研究，2015，32(5)： 1373-1375.

[4] 张润. 基于主成分分析的南京地区空气质量影响因素分析[J]. 科技传播，2014(5)：135-136.

[5] 屈家安，曹杰. 主成分分析与聚类分析在青岛夏季气温变化研究中的应用[J].大气科学学报，2014，37(4)：517-520.

[6] 廖国礼，吴超. 主成分分析法在矿山空气污染监测点优化中的应用[J]. 金属矿山，2005(5)：44-47.

[7] 武松，潘发明，等. SPSS统计分析大全[M]. 北京: 清华大学出版社，2014：334-344.

[8] 刘臣辉，吕信红，范海燕. 主成分分析法用于环境质量评价的探讨[J].环境科学与管理，2011，36(3)：183-186.