例谈数列求和的几种方法
2017-03-17湖北省孝感高级中学李志红
☉湖北省孝感高级中学 李志红
例谈数列求和的几种方法
☉湖北省孝感高级中学 李志红
数列求和具有复杂多变、综合性强、解法灵活等特点,是数列问题中的基本题型,问题技巧性很强,对同学们来说难度较大.不过,只要弄清规律,数列求和问题便可迎刃而解.本文将通过例题简单介绍数列求和的一些基本方法.
一、直接用公式法求和
直接利用等差数列、等比数列的前n项和公式求和,除了等差、等比数列的前n项和公式以外,还要常用公式也应当熟记:


还要记住一些正整数的幂和公式:

例1已知等差数列{an}中,a3a7=-16,a4+a6=0,求其前n项和Sn.
解:因为a4+a6=a3+a7,则a3a7=-16,a3+a7=0,
所以a3=4,d=-2或a3=-4,d=2.
所以数列的前n项和是Sn=n2-9n或Sn=-n2+9n.
二、通项公式法求和
利用通项公式写出数列各项,进而将其和重新组合为可求数列的和.
例2求5,55,555,…的前n项和.
三、裂项相消法求和
把数列的通项拆成两项之差,an=bn-bn+m,n,m∈N,在求和时中间的一些项可以相互抵消,从而求得其和.
例3若{an}是各项均不为0的等差数列,求证:
证明:设等差数列{an}的公差为d.若d=0,要证结论显然成立;若d≠0,得

四、倒序相加法求和
如果一个数列{an}直接求解很困难,它的前n项中首末两端等“距离”的两项的和相等或等于同一个常数,那么求这个数列的前n项和可用倒序相加法.
例4求包含在正整数m与n(m<n)之间的分母为7的所有不可约分数之和.
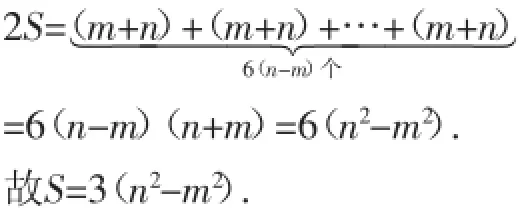
五、错位相减法求和
如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n项和即可用此法来求,如等比数列的前n项和公式就是用此法推导的.
例5已知首项都是1的两个数列{an},{bn}(bn≠0,n∈N*)满足anbn+1-an+1bn+2bn+1bn=0.
(2)若bn=3n-1,求数列{an}的前n项和Sn.
解:(1)cn=2n-1.
(2)得an=bncn=(2n-1)·3n-1,先写出Sn的表达式:
Sn=1·1+3·31+5·32+7·33+…+(2n-1)·3n-1.①
把此式两边都乘以公比3,得
3Sn=1·31+3·32+5·33+…+(2n-3)·3n-1+(2n-1)·3n.②
①-②,得
-2Sn=1+2·31+2·32+2·33+…+2·3n-1-(2n-1)·3n,
-2Sn=(2·30+2·31+2·32+2·33+…+2·3n-1)-(2n-1)·3n-1.
由等比数列的前n项和公式,得
-2Sn=3n-1-(2n-1)·3n-1,
2Sn=-3n+1+(2n-1)·3n+1=(2n-2)·3n+2,
Sn=(n-1)·3n+1.
此题解答步骤多,每一步都容易出错,学生在复习备考中,应彻底弄清、完全掌握,争取做到不丢分.
六、分类讨论法求和
对于有些数列的求和问题,需根据不同的情况进行分类讨论才能正确地获解.
例6求Sn=1-3+5-7+…+(-1)n(2n-1).
解:当n为偶数时,Sn=1-3+5-7+…+[(-1)n-2(2n-3)+
当n为奇数时,Sn=1+(-3+5)+(-7+9)+…+[(-1)n-2
故Sn=(-1)n+1n.
七、分组法求和
一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成,则求和时可得出两个或几个等差数列或等比数列,进而利用等差数列或等比数列的求和公式分别求和,从而得出原数列的和.
例7数列{an}的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=3x+1上,n∈N*.
(1)当实数t为何值时,数列{an}是等比数列?
(2)在(1)的结论下,设bn=log4an+1,cn=an+bn,Tn是数列{cn}的前n项和,求Tn.
解:(1)因为点(Sn,an+1)在直线y=3x+1上,
所以an+1=3Sn+1,an=3Sn-1+1(n>1,且n∈N*).
所以an+1-an=3(Sn-Sn-1)=3an,所以an+1=4an(n>1,n∈N*),a2=3S1+1=3a1+1=3t+1,
所以当t=1时,a2=4a1,数列{an}是等比数列.
(2)在(1)的结论下,an+1=4an,an+1=4n,bn=log4an+1=n,cn=an+bn=4n-1+n,
所以Tn=c1+c2+…+cn=(40+1)+(41+2)+…+(4n-1+n)
=(1+4+42+…+4n-1)+(1+2+3+…+n)

八、待定系数法求和
当求和过程中一些量直接求比较困难时,可以采取待定系数的方法,先设出相应的量,再列方程求解.
例8数列{(2n-1)·3n}的前n项和Sn=________.
解:设等差数列{an}的公差为d,等比数列{bn}的公比为q(q≠1),得
am·bm=[a1+(m-1)d]·b1qm-1(m=1,2,…,n).
先用错位相减法求数列{an·bn}的前n项和Sn:


所以有下面的结论成立:
若{an},{bn}分别是等差数列、等比数列(其公比q≠1),且a1,b1均是与n无关的常数,则数列{an·bn}的前n项和Sn=(an+b)qn-b,其中a,b是与n无关的常数.
由此结论就可以用待定系数法快速求解本题:可设Sn=(an+b)·3n-b(其中a,b是常数),
可得S1=3,S2=3+27=30,所以解得所以Sn=(n-1)·3n+1+3.
九、求导法、积分法求和
观察所给式子的特征,有时可以通过求导解决.
(3)求数列{(2n-1)·3n}的前n项和Sn(例6).
解:(1)当x=0时,显然成立;当x≠0时,由等比数列的前n项和公式知,待证结论也成立.
(2)视(1)的结论为两个函数相等,两边求导后即得欲证成立.
(3)(2n-1)·3n=6(n·3n-1)-3n.
由(2)的结论中令x=3,得数列{n·3n-1}的前n项和为,又数列{3n}的前n项和为所以数列{(2n-1)·3n}的前n项和为(n-1)·3n+1+3.
数列求和的方法千变万化,但是数学试题具有“源自教材,但高于教材;题在书外,但是根在书内”的特点,因而在课堂解题教学活动中,需要时刻注意立足教材,回望教材,“一切从教材中来,一切又回到教材中去”,从教材提炼数学思想方法,使得学生体会到解决问题的思路、策略、方法源自教材,从而有效地提高创新能力.在平时的解题过程中不断总结,才能取得长期的收益.
