基于数学核心素养的“一元二次不等式的解法(1)”教学设计
2017-03-17上海大学附属中学顾晨曦
☉上海大学附属中学 顾晨曦
基于数学核心素养的“一元二次不等式的解法(1)”教学设计
☉上海大学附属中学 顾晨曦
一、引言
高中数学新一轮课标的修订接近尾声,本次修订的总目标是发展“四基、四能、形成六大数学核心素养:数学抽象,逻辑推理,数学建模,数学运算,直观想象,数据分析”.在新课改下数学课堂教学应该呈现什么?应该教什么?怎样才能促进形成六大数学核心素养?
这些都是需要探讨的问题.本文尝试针对沪教版高一第一学期2.2一元二次不等式的解法(第一课时),基于数学核心素养进行教学设计,以期初探高中新课标下教学设计讨论的大门,也为其他关于数学核心素养问题的讨论起抛砖引玉的作用.
二、设计目标和思路
本课的设计力求通过实际问题的解决提升学生的操作数据、分析数据的能力,在这个过程中,培养数学建模、直观想象、数据分析的核心素养;通过图形计算器绘制函数图像,编制不等式求解的数学活动,让学生从探索问题中使用归纳推理,完成从具体问题到数学方法的归纳过程,贯穿一元二次不等式与二次函数,一元二次方程之间的内在联系,进行合理的推断和直观想象;利用学生当堂生成的题目,进行数学运算的训练,掌握一元二次不等式的解法.
三、教学过程
1.引入:利用数学实验构建数学模型,初探数据分析的魅力
问题:一家面粉生产厂引进一条生产线,由于受设备成本、人工、不同产量运输方式的不同等因素影响,这条生产线产出的面粉x吨,与每吨面粉的收益y万元之间有如下关系:
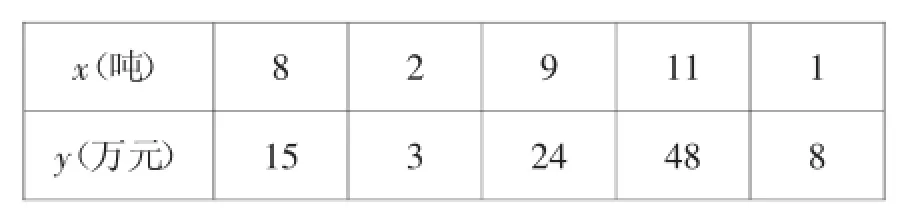
x(吨)829111 y(万元)15324488
如果你是该厂厂长,请你决定面粉产量在什么范围内可盈利?
利用图形计算器(TI-nspire CX-C CAS)输入数据,得到散点图,利用回归分析,拟合得出图像解析式,(见下图)根据实际意义,得到不等式:x2-8x+15≥0.



设计说明:俗话说“好的开始是成功的一半”,新课程的引入往往是最值得推敲的部分.对于本节课的引入,是采取情境引入法?还是直接利用一元二次方程的定义,将“等号”改为“不等号”类比引入?教材的设计采用了前者,意图以期学生能把实际问题抽象为数学问题,并建立一元二次不等式求解,体会一元二次不等式解法的必要性.
在尊重教材对于核心素养培养的基础上,笔者在引入时思考,既然需要“建模”,不如将“建模”进行到底.不等式关系如何得出的?在学生今后面临的实际工作和生活中,没有人会给你明确的函数关系式,你面对的是信息,是数据.这时,数据分析能力,数学抽象能力就起了很大作用.所以,笔者在引入中,采取只给出情境和数据的方法,抓住这个难得的机会,利用TI-nspire手持机,让学生体会了一把真正的建模,在众多未知因素面前,体会到现代技术在数据分析功能上的强大作用.
虽然在技术层面上,受课堂时间和高一学生知识储备所限,这个建模不太严格,有些理想化,然而“不入园林,怎知春色如许?”本节课对于数学建模走入常规课堂做了一个初探.学生对于这种引入,也感到新颖,并且理解得也较有深度.在课堂上,学生主动提出对于模型中x取值范围为正数的修正,在学生的对话中确定了范围.在课后的统计中,100%的学生认为此课的引入形式具有创新性,84.2%的学生认为这种引入相比传统形式“培养了数学建模的能力”,15.8%的学生表示对这个问题“说不清”,没有学生在这个问题上选“否”.
2.新授:没有例题的“例题讲解”,逻辑推理得出解法
本节课对于一元二次不等式解法的讲解,大胆采用了没有一道教师预设例题的方法,由学生根据使用计算器绘制的函数图像编制不等式形成例题,结合TI-nspire图像跟踪功能的使用,直观地呈现了符合要求的解的区间.以下呈现几个典型图形以及相关问题串.

针对每个图形,教师与学生依如下问题串对话:
请你根据这个函数图像,编制一个不等式.
x轴上方(或下方)的点有什么共同特征?
这些点的横坐标代表什么意义?
它们在x轴上投影的范围有什么特点?
你能由此得到相应的不等式的解集吗?
设计说明:在解法的教授中,侧重图像法,充分体现数形结合的思想,体现数学符号语言和图形语言的翻译.学生利用计算器辅助学习,自主编制题目并求解,这些新鲜出炉的、自己创造的题目,更能引起学生的学习欲望.令课堂教学变得灵活生动起来,让学生亲自体验到自己是课堂的主体,将数学运算的核心素养渗透到课堂的活动当中.
利用问题串,将学生的思维过程层层解构,再在解法的得出中进行重组,在从特殊到一般的方法总结过程中,培养逻辑思维和推理能力.
在课堂上,即使是学习能力偏弱的学生,在图形和问题串的帮助下,可以自行得出不等式的解集.笔者还提了这样一个问题,“请根据图形构建一个解集为一个区间的不等式”,这个问题在课堂上激起了小小的浪花,学生惯性思维于解决诸如y>0的问题,对于逆向的构造问题,势必陌生.此问题正是一个良好的训练机会,契合了依据逻辑规则推出一个命题的逻辑推理要求.
3.练习:再探数学实验,技术支撑你我的梦想
在本节课的练习部分,解含参不等式x2-3ax+2a2<0借助图形计算器,通过游标功能改变参数a的取值,得到不等式的解集.(见下图)


设计说明:含参数的不等式解法一直是学生学习中的难点,而数学实验作为数学建模的重要组成部分,随着计算机的发展,日益凸显其作用.根据数学教育家弗赖登塔尔所提倡的教学理念:“学一个活动最好的方法就是做”当代数学教育不能仅教给学生现成、静态的数学,如何让学生通过再创造体会到作为活动的数学?体会到数学知识的发现过程?数学实验是一个绝佳的实施平台.
通过图形计算器中的游标功能,做出相应的函数图像,学生在实验中发现a的取值范围直接影响了题目的答案,形成分类讨论的数学思想.这个过程所留下的印象在学生脑海中是深刻的,虽然花费了一定的时间,然而浓厚的兴趣常常是维系长久的有创造的研究和学习的主要动力,在课堂的主阵地上给予学生探索的时间和机会,这个时间应该说花得值.
4.小结:智能计算思维立意下的方法总结,授之于“方法”之“渔”
本节课的小结突破传统,使用如下求解一元二次不等式的程序框图进行方法总结:

设计说明:
智能计算思维被界定为一种运用计算机科学基本概念解决问题、设计系统以及理解人类行为的方式方法.在现代社会中,它是一种每个人都应该有的应用态度和技能.建立在学生信息课所学的基础上,利用流程图总结一元二次不等式的解法,意在示范学生一种解决问题的思维过程,是一种可得到通法通则的方法.如果说题目的解决是“授之于鱼”,方法的教授是“授之于渔”,那么思维的过程则是形成方法的过程,“授之于渔”的“渔”.在这个过程中,通过分类,解决疑难,排除故障.在讨论中修正解法,理解内部的关系,形成系统思维的习惯.
四、教后反思
教学中,学生对于计算器使用的掌握比预想中要好,没有因为计算器操作出现不必要的时间浪费.图形计算器在本节课中让学生深刻体会到了数学建模的强大作用,体会到了数形结合解题的必要性和便捷性,课堂对话中发现学生对于图形法解不等式也理解得比较到位.当堂检测中,学生可以独立完成基础题目,并自己纠错和订正,说出错误原因和正确做法,基本达到了本堂课的教学目标.对于Δ=0,Δ<0的题目,学生掌握的不是太好,出错率较高,约50%,在教材的设计上,这原属于第二课时的内容,在重组教材时,笔者将其放在了第一课时.这提示我们在重组教材时,应关注学生在思维层次上的不同,给予学生更充分的内化时间.
本节课主要存在的问题是,引入部分还是略长,所占篇幅削弱了正题的讲解,是否应该考虑更加简洁实用?另外,也有教师提出建议,使用图形计算器,便捷了,但削弱了对学生画图能力的训练,毕竟考试时无法使用,所以在此处使用是否是一个好的选择?其实,这些声音的根本,求问的是一个一直困扰一线教师的问题:应试与能力,如何双赢?路漫漫其修远兮,吾将上下而求索.
