不平等的度量指标与分解方法的梳理及展望

张世君

山西财经大学统计学院

不平等的度量指标与分解方法的梳理及展望

张世君

山西财经大学统计学院

不平等问题是一个非常普遍而又值得研究的社会问题。本文在不平等测度思想上，系统梳理了不平等测度的指标以及不平等的分解方式。详细讨论了各指标的特性、适用范围和局限性，并指出在未来不平等测度中应该着重研究的方向。

不平等；指标分解；基尼系数；夏普里分解

一、不平等指标

(1)极差。极差即最小收入到最大收入的距离，极差作为不平等度量指标有着明显的缺陷，它忽略了两个极值之间的所有分配情况。

(2)方差。方差是一个常用的统计量，它将收入与平均值的离差平方后相加，更加凸显了对平均值的离散程度。方差符合庇古-道尔顿转移支付原理。缺点在于方差大小依赖于平均收入水平，一种分配可能比另一种有更大的相对差距，但却具有更小的方差。

(3)变异系数。对方差稍加变动即可得到变异系数，变异系数克服了方差的上述缺陷并保留了符合转移支付原理的品质。变异系数为方差的平方根处以收入均值。

(4)对数方差。比起真实的方差或标准差来说，对数形式的一种好处是它消除了测度单位的任意性和绝对水平，构造方式是所有指标先取对数，在计算方差。

(5)基尼系数。基尼系数是当前测度不平等使用最为广泛的指标之一。基尼系数可由洛仑兹曲线转化而得到。

(6)广义熵指数族。泰尔引用了信息论中“熵”的概念，提出了泰尔指数作为测度不平等的一种方法。在此基础上Cowell定义了更一般性的广义熵指数族。

(7)不平等指标性质。上述指标各自的满足的性质如表1所示：

二、不平等的分解

1.按人口子群分解

人口子群分解即先将人口按照性别、区域、社会阶层等属性分组，然后将总的不平等分解为小组间不平等与小组内不平等的形式。

组间不平等：当每组内部皆为平等分配，总的不平等表现为小组间平均收入不平等的时候，认为只存在组间不平等而不存在组内不平等，因此即为反应组间不平等。

组内不平等：当小组间人均收入都相同时，此时认为不存在组间不平等，总的不平等表现为小组内部分配不平等的加权和。反应的即为组内不平等。

Shorrocks(1980，1984)证明了唯一满足人口子群分解性质的相对指标体系为广义熵指数族：

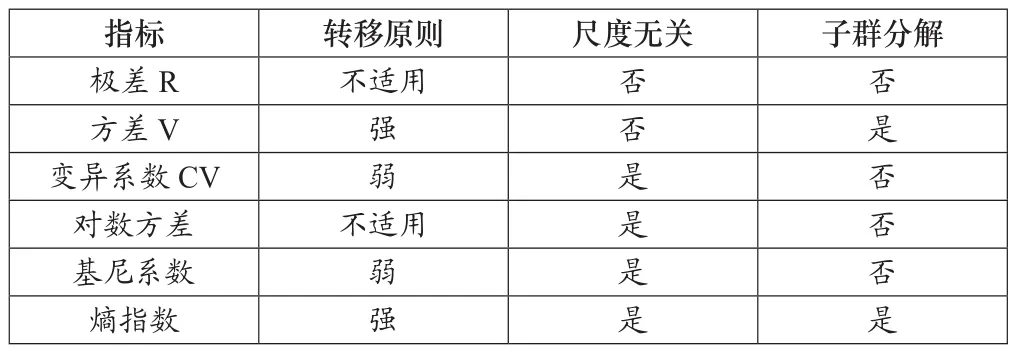
表1

2.按影响要素分解

夏普里分解(Shapley decomposition)：考虑一个统计指标I，其值完全决定于m容量的因子集，可以写作。是影响因子的标量或向量。用F(S)表示当因子被剔除时I的取值，据此可以很方便的根据因子集K和函数定义一个模型结构，记为＜K，F＞。由于因子集全部解释了I，因此可以得到，即当所有因子被剔除时指标I为0。

分解规则必须满足如下因素：首先，在任何给定因子贡献的意义上，其应当是对称的；其次，分解必须是绝对的并具有分解可加性，即：。

到此为止，最自然的分解为考虑各影响因子边际影响如下：

该分解具有对称性质，但是分解值非绝对，它存在路径依赖问题。即从因子集中剔除因子的顺序会影响到最终分解结果。

若要取得绝对的分解值解决路径依赖问题，只需考虑所有可能的因子排序并且求得期望值即可，m因子剔除排序共有m!种可能，则产生最终分解规则 。

三、结语与评论

本文系统梳理了不平等测度中不同的测度指标及其各自的性质，并且也整理了目前较为新颖的分解方式。从指标特性上来看，熵指数由于其适用性广泛且具有可分性，因此在研究不平等的跨人群比较或跨区域比较中使用率较高；而基尼系数由于其和洛伦兹曲线的直观联系使得在一般测度时使用率更为广泛。

在不平等的分解方面，原先的分解主要是依靠指标自身的分解性质来进行，如果指标本身不可分解则倾向于使用其他指标。而夏普里分解的方法则是针对所有指标都可以进行分解，因此很大程度上解决了不平等指标的分解问题，本文也是推荐在指标不可分解时使用夏普里分解方法。

[1]阿玛蒂亚森，论经济不平等/不平等之在考察[M]，社会科学文献出版社，第一版

[2]万广华，不平等的度量与分解[J].经济学(季刊)，2008，8(1): 347-368

[3] Mauro Mussini，A subgroup decomposition of theinequality change over time[J]，Applied Economics Letters，2013，20，P386-390