螺旋槽干气密封压差扰动下的瞬态特性研究

胡松涛,黄伟峰,刘向锋,王玉明

(清华大学 摩擦学国家重点实验室，北京 100084)

螺旋槽干气密封压差扰动下的瞬态特性研究

胡松涛,黄伟峰,刘向锋,王玉明

(清华大学 摩擦学国家重点实验室，北京 100084)

干气密封的瞬态特性是密封动力学研究中的重要内容，而现有研究主要关注于密封稳态特性的研究。本文针对密封内外压差波动这一典型工况开展仿真分析，研究螺旋槽干气密封在扰动工况下的瞬态特性。计算中，将润滑方程、接触方程与动力学方程耦合求解，以轴向膜厚、角向偏摆角、泄漏率和端面接触载荷为主要指标。结果表明：密封侧压力突降相比较于突升，更易引起密封环震荡，但后者更易诱发端面接触。对于扰动引起的瞬态震荡，密封的角向行为引起震荡时间的延长与震荡幅值的减小，其与轴向行为共同决定端面接触的可能性。动静环间的极薄气膜不仅将动环的行为传递给静环，同时通过弱化轴向与角向行为的相互影响来缓解扰动所引起的密封瞬态震荡。

螺旋槽;干气密封;瞬态特性;扰动

1 前言

螺旋槽干气密封(图1)作为一种典型的气体非接触式机械密封，在泵、压缩机等旋转机械中得到广泛的应用。合理设计的干气密封需要依靠其动态特性，在满足较小泄漏量指标的同时，避免端面接触的发生。现有的螺旋槽干气密封动态特性研究，多关注于密封在稳定运行状态下的性能分析。事实上，干气密封的运行环境极为复杂，往往面临着变工况、多干扰工况等扰动因素的影响。因此，在设计及研究螺旋槽干气密封时，需研究密封在扰动工况下的瞬态特性。

图1 螺旋槽干气密封结构示意

机械密封的动态特性研究在Etsion后逐渐成为热门研究领域[1～3]，考虑其可压缩性与非线性特征，目前全数值方法与半解析方法被视为主要研究手段[4～15]。Shapiro和Colshe通过分别独立求解润滑方程和动力学方程来准动态地研究一种飞机引擎轴端气体密封的动态特性[4]。Miller和Green提出一种将气体润滑方程和动力学方程转化为空间格式，进而实现同步求解的数值方法[5]。该方法随后被Green和Barnsby用于研究气体锥度密封在稳定运行状态下的动态特性[6,7]。虽然全数值方法能详细、准确地提供干气密封的动态特性，但其需要耗费大量计算时间，效率较低，且对于硬件的要求较为苛刻。对于大批量、高密度的数值仿真计算工作，半解析方法更为有效。Zirlelback和San Andres使用摄动法计算气膜轴向的线性化刚度与阻尼系数[8]，进而讨论了密封参数对于干气密封动态特性的影响[9]。Ruan进一步耦合密封角向行为[10]，得到气膜轴向和角向的线性化刚度与阻尼系数以完善摄动法。与此同时，在Elrod等于气体轴承领域提出阶跃法后[11]，Miller和Green进一步提出了适合于螺旋槽干气密封的半解析方法[12]。可以发现，上述干气密封的动态特性研究主要关注于密封的稳定性与追随性，并未考虑端面接触问题。

事实上，非接触式干气密封在启停阶段必然存在端面接触[13]，其在作业阶段受扰时亦存在发生端面接触的可能性[14]。在粗糙峰接触研究领域，Greenwood和Williamson率先提出了粗糙表面间的弹性粗糙峰接触模型(GW模型)[15]。Chang、Etsion和Bogy基于GW模型，利用塑性变形体积守恒，提出了粗糙表面间的弹塑性粗糙峰接触模型(CEB模型)[16]。为克服上述统计学模型对于分形表面的不足，Majumdar和Bhushan利用Weierstrass-Mandelbrot函数建立了第一个粗糙表面间的分形粗糙峰接触模型(MB模型)[17]。Morag和Etsion认为MB模型中随接触载荷增加粗糙峰由塑性变形转化为弹性变形的结论与经典的接触机理相违背[18]。他们通过修正粗糙峰的变形量，建立起单一粗糙峰的修正弹塑性粗糙峰接触模型。这些粗糙峰接触模型已经逐步被应用于干气密封的动力学研究。Harp和Salant将Abbott-Firestone塑性粗糙峰接触模型应用于轴向动力学研究[19]。Green则将CEB模型应用于气体锥度密封的启动特性研究[20]。在Ruan将 CEB模型应用于螺旋槽干气密封启停特性的研究后[21]，Hu等先后采用CEB与MB模型开展动力学研究[22,23]。

现有的干气密封动态特性研究大多关注于密封稳态特性的研究，少量涉及启停阶段的瞬态特性，缺乏密封在扰动工况下的瞬态特性研究。因此，本文针对密封内外压差波动开展仿真计算，分析螺旋槽干气密封在扰动工况下的瞬态特性。

2 研究方法

2.1 密封全数值动力学模型建立

对干气密封的结构进行简化，将动环与静环的几何形状简化为圆环，建立如图2所示的动力学模型。

图2 干气密封动环结构与密封动力学模型示意

动环的环面上开有N个深度为δg的螺旋槽，螺旋角为α，环的内径、外径及槽坝边界分别为ro,ri和rg。进一步，定义β= (rg-ri)/(ro-ri)，λ=Wg/(Wg+Wl)。将动环偏摆角γr、静环偏摆角γs及两者的相对偏摆角γrel分解为X轴和Y轴的分量[5,10,12,21]：

(1)

式中ω——旋转轴转速t——时间

此时，静环上任意点(x,y)的气膜厚度h为：

h(x,y)=c+yγx-xγy-γrycos(ωt)

+γrxsin(ωt)-zr+〈δg〉

(2)

式中c——动静环间的中心膜厚zr——动环的轴向窜动 〈δg〉——螺旋槽深度

对于动静环间的气膜，假设其为理想气体且等温，忽略动静环表面形貌影响，则可使用可压缩形式的Reynolds方程建立气膜的流场模型[5～7,10,12,20～23]：

(3)

式中p——气膜压力分布μ——气体动力粘度r——半径iθ——θ方向的单位矢量

流场模型的边界条件为：

(4)

考虑支撑弹簧和副密封提供的刚度和阻尼，建立静环的轴向-角向动力学模型[5,10,12,21,22]：

(5)

式中m,I——静环的质量和转动惯量Fclosing——静环处于平衡位置时施加在其背面的闭合力，由压差和柔性装置共同构成

Fg——气膜开启力

Fc——端面接触力

Mgx,Mgy,Mcx,Mcy——Fg,Fc在X与Y方向的弯矩

Msi——静环由于弹簧不均或安装误差等受到的弯矩，假设其完全作用在X轴上，其与静环静态偏摆角γsi的关系为Msi=ksγγsi

ksz,csz——支撑弹簧和副密封在轴向上的刚度和阻尼

ksγ，csγ——角向的刚度和阻尼，ksγ，csγ可以依据Green和Etsion的模型建立[24]：ksγ=kszro2/2，csγ=cszro2/2

式(5)中，广义载荷Fg，Fc，Mgx，Mgy，Mcx和Mcy可通过在名义接触面积An(密封面积)上对气膜压力分布p与接触载荷分布pc积分获得：

(6)

针对密封端面接触，本文采用已得到广泛使用的CEB模型。在CEB模型中，粗糙峰平均接触压力pc为[16,25]：

(7)

式中ηs——粗糙峰密度E——Hertz弹性模量Rs——粗糙峰平均曲率半径ωc——由弹性进入塑性的临界形变量zs——粗糙峰高度φ()——粗糙峰概率密度函数(本文采用高斯分布)

K——最大接触压力因子

H——软材料硬度

2.2 模型计算流程

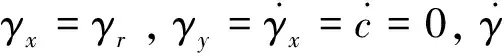
3 参数研究

表1为基础参考算例。表2列出了6个参数研究算例，每个算例包含2列。

表1 基本算例参数

与算例A相比，算例B只考虑密封轴向的动力学行为。以4种典型参数作为动态特性的评价指标：中心膜厚c用于表征静环的轴向位置，角向偏摆角γrel用于表征静环的角向追随性能，泄漏率Q用于表征密封性能，接触载荷Fc用于表征密封间的接触性能。

图3示出了瞬时的压差波动诱发中心膜厚(图3(a))、角向偏摆角(图3(b))、泄漏率(图3(c))与端面接触载荷(图3(d))的震荡。针对图3(a)～(c)，比较算例A1与算例A2发现，扰动幅值越大，震荡越激烈。比较算例A1与算例A3发现，尽管两者外压波动的比例相同，但算例A3震荡的幅值较大，震荡次数较少。其原因为：算例A1中，外压瞬时变为10 MPa，此时，静环受到的闭合力与开启力都极大，限制了静环震荡的幅值，但同时增加了震荡次数；而算例A3中，外压瞬时变为0.1 MPa，静环被流体开启力推离动环，而此时，静环受到的开启力较小，闭合力仅由柔性装置提供，静环震荡不受限制，震荡幅值较大但更易达到稳定状态。由此可见，降压比升压更易造成静环震荡。然而，由于降压会引起中心膜厚的增加，增压会引起中心膜厚减小，因此增压更易诱发端面接触(如图3(d))所示，算例A3并未出现端面接触)。此外，图3(c)特别给出了算例A1在稳定状态(0.036～0.038 s)下的内外径处泄漏率的变化，结果表明，内外径处泄漏率存在差异，该差异由气膜的挤压效应造成，通过挤压效应，气膜将动环的运动传递给静环。进一步研究发现，静环的动力学行为的震荡诱发其外径处泄漏率出现较大的震荡，但其内径处泄漏率震荡极小，表明气膜的挤压效应同时有助于缓解密封震荡。

图4以算例A1与算例B1为例，讨论角向行为对于静环整体动态特性的影响。图中，算例A1的轴向膜厚、泄漏率与端面接触载荷的震荡幅值较小，但震荡持续时间较长，由此可见，密封的角向行为可通过延长震荡时间的方式来减小震荡幅值。

(a) 中心膜厚c

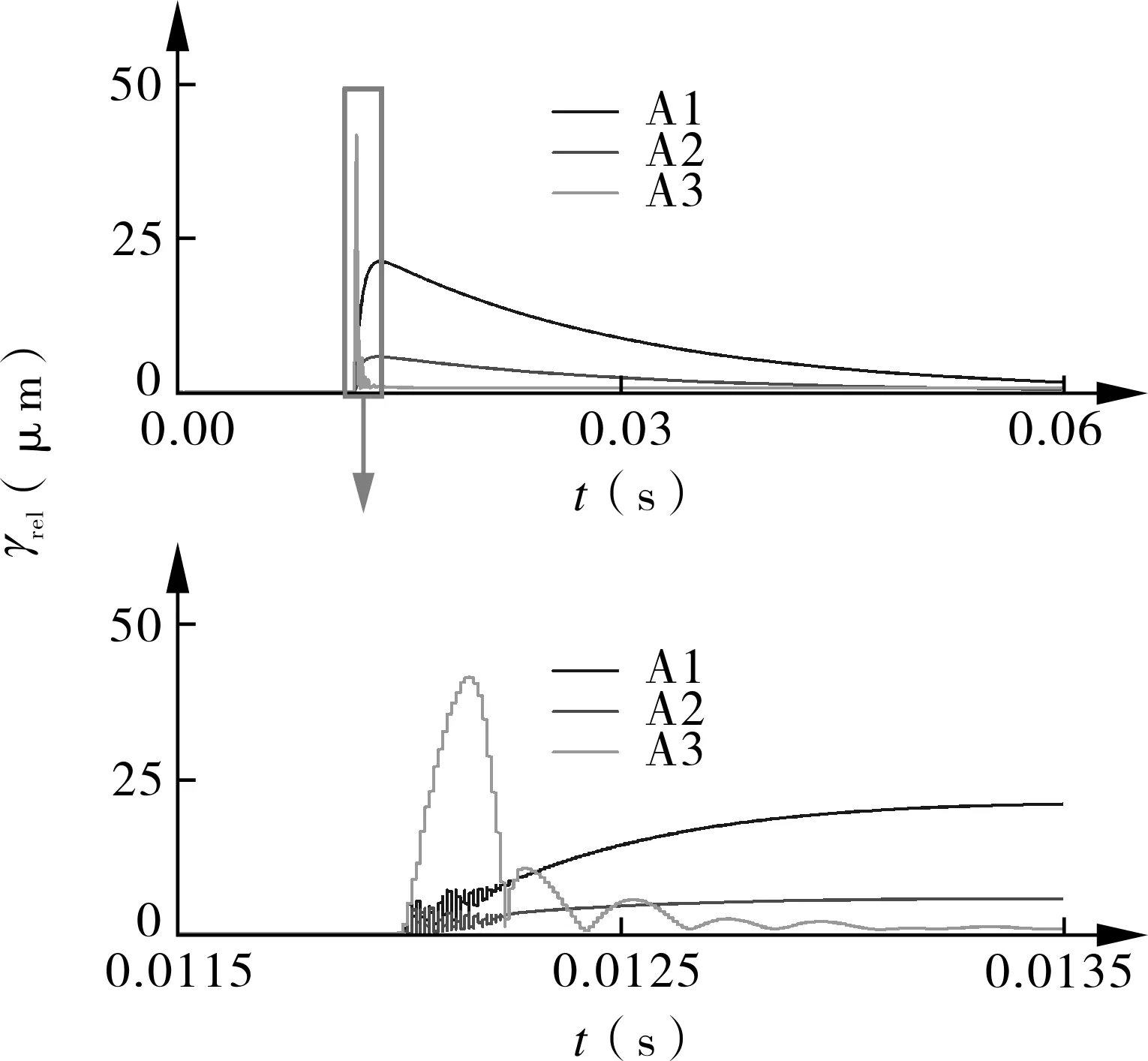
(b)角向偏摆角γrel

(c)内外径处泄漏率Qi和Qo

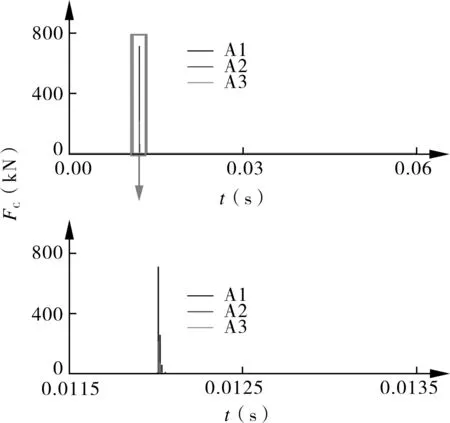
(d)端面接触载荷Fc

(a)中心膜厚c

(b)内径处泄漏率Qi

(c)端面接触载荷Fc

4 结论

(1)密封侧压力突降相比较于突升更易引起密封环震荡，但后者更易诱发端面接触。

(2)对于扰动引起的瞬态震荡，密封的角向行为引起震荡时间的延长与震荡幅值的减小。鉴于其与密封轴向行为共同决定端面接触的可能性，在密封研究设计时应该给予重视。

(3)动静环间的极薄气膜不仅将动环的行为传递给静环，同时通过弱化轴向与角向行为的相互影响来缓解扰动所引起的密封瞬态震荡。

[1] Etsion I.A review of mechanical face seal dynamic [J].Shock and Vibration,1982,14(3):9-14.

[2] Etsion I.Mechanical face seal dynamics update [J].Shock and Vibration,1985,17(4):11-16.

[3] Etsion I.Mechanical face seal dynamics 1985-1989 [J].Shock and Vibration,1991,23(4):3-7.

[4] Shapiro W,Colsher R.Steady-state and dynamic analysis of a jet engine,Gas Lubricated Shaft Seal [J].ASLE Transactions,1974,17(3):190-200.

[5] Miller B A,Green I.Numerical formulation for the dynamic analysis of spiral-grooved gas face seal [J].Journal of Tribology,2001,123(2):395-403.

[6] Green I,Barnsby R M.A simultaneous numerical solution for the lubrication and dynamic stability of noncontacting gas face seals [J].Journal of Tribology,2001,123(2):388-394

[7] Green I,Barnsby R M.A parametric analysis of the transient forced response of noncontacting coned-face gas seals [J].Journal of Tribology,2002,124(1):151-157.

[8] Zirkelback N,Andres L S.Effect of frequency excitation on force coefficients of spiral groove gas seals [J].Journal of Tribology,1998,121(4):853-863.

[9] Zirkelback N.Parametric study of spiral groove gas face seals [J].Tribology Transaction,2000,43(2):337-343.

[10] Ruan B.A Semi-analytical solution to the dynamic tracking of non-contacting gas face seals [J].Journal of Tribology,2002,124(1):196-202.

[11] Elrod H G,Mccabe J T,Chu T Y.Determination of gas-bearing stability by response to a step-jump [J].Journal of Lubrication Technology,1967,89(4):493-398.

[12] Miller B A,Green I.Semi-analytical dynamic analysis of spiral-grooved mechanical gas face seals [J].Journal of Tribology,2003,125(2):403-413.

[13] Huang W,Lin Y,Liu Y,et al.Face rub-impact monitoring of a dry gas seal using acoustic emission [J].Tribology Letters,2013,52(2):253-259.

[14] Huang W,Lin Y,Gao Z,et al.An acoustic emission study on the starting and stopping processes of a dry gas seal for pumps [J].Tribology Letters,2013,49(2):379-384.

[15] Greenwood J A,Williamson J B P.Contact of nominally flat surfaces [J].Proceedings of the Royal Society,London,1966,A295:300-319.

[16] Chang W R,Etsion I,Bogy D B.An elastic-plastic model for the contact of rough surfaces [J].Journal of Tribology,1987,109(2):257-263.

[17] Majumdar A,Bhushan B.Fractal model of elastic-plastic contact between rough surfaces [J].Journal of Tribology,1991,113(1):1-11.

[18] Morag Y,Etsion I.Resolving the contradiction of asperities plastic to elastic mode transition in current contact models of fractal rough surfaces [J].Wear,2007,262(5):624-629.

[19] Harp S R,Salant R F.Analysis of mechanical seal behavior during transient operation [J].Journal of Tribology,1998,120(2):191-197.

[20] Green I.A transient dynamic analysis of mechanical seals including asperity contact and face deformation [J].Tribology Transaction,2002,45(3):284-293.

[21] Ruan B.Numerical modeling of dynamic sealing behaviors of spiral groove gas face seals [J].Journal of Tribology,2002,124(1):186-195.

[22] Hu S,Huang W,Liu X,et al.Influence analysis of secondary O-ring seals in dynamic behavior of spiral groove gas face seals [J].Chin.J.Mech.Eng.2016,29(3):507-514.

[23] Hu S,Huang W,Liu X,et al.Numerical model for dynamic behavior of spiral groove gas face seals using fractal contact model [C].The 70th STLE Annual Meeting,Dallas,May 17(21,2015,150.

[24] Green I,Etsion I.Stability threshold and steady-state response of noncontacting coned-face seals [J].ASLE Transactions,1985,28(4):449-460.

[25] Hu S,Brunetiere N,Huang W,et al.Continuous separation method for characterizing and reconstructing bi-gaussian stratified surfaces [J].Tribol.Int.,2016,102:454-462.

Transient Response Analysis of Spiral Groove Gas Face Seals under Pressure-drop Fluctuation

HU Song-tao,HUANG Wei-feng,LIU Xiang-feng,WANG Yu-ming

(State Key Laboratory of Tribology,Tsinghua University,Beijing 100084,China)

Transient performance under fluctuation conditions is important component of the dynamic behavior of spiral groove gas face seals,the current research for which mainly focuses on the steady-state performance.A research on the transient response to pressure-drop fluctuation is performed.The results show that the decrease of sealed pressure will cause greater oscillations in the motions while the increase of sealed pressure is easier to cause face contact.Angular motions will reduce the oscillation amplitude but prolong the oscillation time.It importantly affects the occurrence of face contact together with the axial motion.The squeeze flow effect of gas film can not only transfer the motion of the rotor to the stator,but also reduce the interactive influence of the axial and angular modes to relief oscillations caused by fluctuations.

spiral groove;gas seal;transient response;fluctuation

1005-0329(2017)02-0022-06

2016-07-05

2016-08-22

国家973重点基础研究项目(2012CB026003);国家重大科技专项(ZX06901);国家科技支撑计划项目(2015BAA08B02)

TH136

A

10.3969/j.issn.1005-0329.2017.02.005

胡松涛(1989-)，男，博士研究生，主要从事机械密封方向的研究，通讯地址：100084 北京市清华大学机械工程系李兆基科技大楼A1046-2，E-mail：HSTTAOTAO@163.com。