dq0坐标系下微网电压电流双闭环下垂控制方法及其逆变器设计

李燕青，王子睿

(华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003)

dq0坐标系下微网电压电流双闭环下垂控制方法及其逆变器设计

李燕青，王子睿

(华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003)

下垂控制是在微网中广泛使用的一种控制策略，下垂控制的逆变器联网运行时，微源输出功率为下垂曲线在频率等于50 Hz处的功率值，逆变器相当于恒功率输出。在介绍了下垂控制的基本原理和具体实现方法的情况下，研究了下垂控制的逆变器并网运行时的特性，得出了线路阻抗和下垂系数均象征着并网过程中系统阻尼的结论，设计了下垂控制的功率控制器和逆变器输出端滤波器的参数取值，利用matlab模型对设计进行仿真,并设计了下垂控制离网运行时的频率恢复控制方法。

下垂控制；联网运行；解耦控制；双闭环控制；稳定；频率

0 引 言

下垂控制属于微网对等控制范畴，其宗旨是不借助互联线仅根据逆变器本地电压电流信息实现各逆变电源之间的功率分配，当微网系统负荷变动时，保证负荷点电压幅值和频率处在允许范围内。

下垂控制用于微网并网时具有无需改变控制策略的优点[1]，并网后逆变电源会发出电网额定频率处对应的有功功率，相当于恒功率控制[2]。现有文献已经对下垂控制策略做了大量的研究，有通过建立微网孤岛运行时下垂控制的小信号模型来研究系统某一参数变化时对系统特征根轨迹的影响，从而找到影响系统稳定性的关键因素，为控制器参数设计找到依据，如文献[3-6]；有对下垂控制的电压电流控制器的设计做改进以提高控制性能的，如文献[7]；也有文献研究逆变器并网性能的，如文献[8]研究了并网条件了PQ控制和PV控制的动态性能，得出了PV控制瞬时性能优于PQ控制的结论；文献[9]则在忽略电压电流控制环和滤波器动态效应下建立了采用下垂控制的三相逆变器与配电网(假设为无穷大系统)并联的瞬时数学模型，分析了并网过程中频率的变化情况。

本文针对下垂控制的并网特性做了专门研究，本文首先介绍了下垂控制的基本原理，介绍了下垂控制各个模块的具体实现，然后设计了下垂控制的功率控制器和逆变器输出端滤波器的参数取值，从闭环系统带宽的角度设计了dq0坐标系下电压电流双闭环控制器的控制参数，利用matlab模型对设计出的下垂控制器进行了微网离网和联网运行条件下的仿真，又针对离网运行时微网负荷过大会导致系统频率偏差过大的缺陷，设计了下垂控制离网运行时的频率恢复控制方法，最后总结了全文。

1 下垂控制的基本原理

传统下垂控制的整体结构图如图1所示，按照功能可分为三个模块：功率控制器、电压控制器、电流控制器[10]。

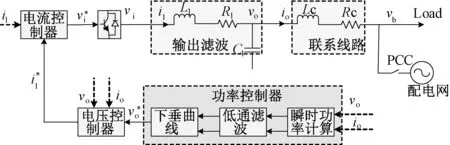
图1 下垂控制整体结构图Fig.1 Droop control overall structure diagram

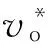
下面对下垂控制各模块的具体工作过程做一介绍：(以有功频率调节为例)

如图2所示，假设系统初始运行与A点，有功为P0，频率为ω0。现由于某种原因系统中有功负荷增加，功率控制器检测到负荷增大，经过下垂曲线降低参考电压的输出频率，电压控制器和电流控制器按照新给出的参考电压共同作用，使逆变器输出端电压频率降低，在一般交流系统里，系统传输的有功与线路两端电压相角差有关，进而与电压频率有关，当输出端电压频率降低时，逆变器发出的有功功率一般会降低，这一趋势与原来系统负荷增加的趋势相反，形成一个负反馈，当两个趋势达到平衡时，系统即达到新的稳态运行点A’，有功功率为P1，频率为ω1。对于无功与电压的调节具有相似的道理。

由以上的分析过程可以看出，下垂控制得以保持系统稳定的一个前提是在局部范围内系统中有功功率具有随着频率下降而降低的趋势，无功功率具有随着电压幅值下降而降低的趋势，这两个关系也是在传统电力系统中调节发电机端电压以适应负荷变化并保持系统稳定的依据。

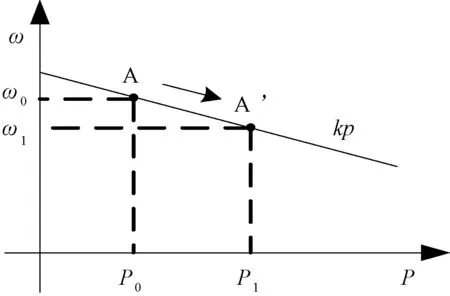
图2 有功频率调节示意图Fig.2 Schematic diagram of active power frequency regulation

2 下垂控制的具体实现

2.1 功率控制器

按照功率控制完成的功能，其内部结构如图3所示。

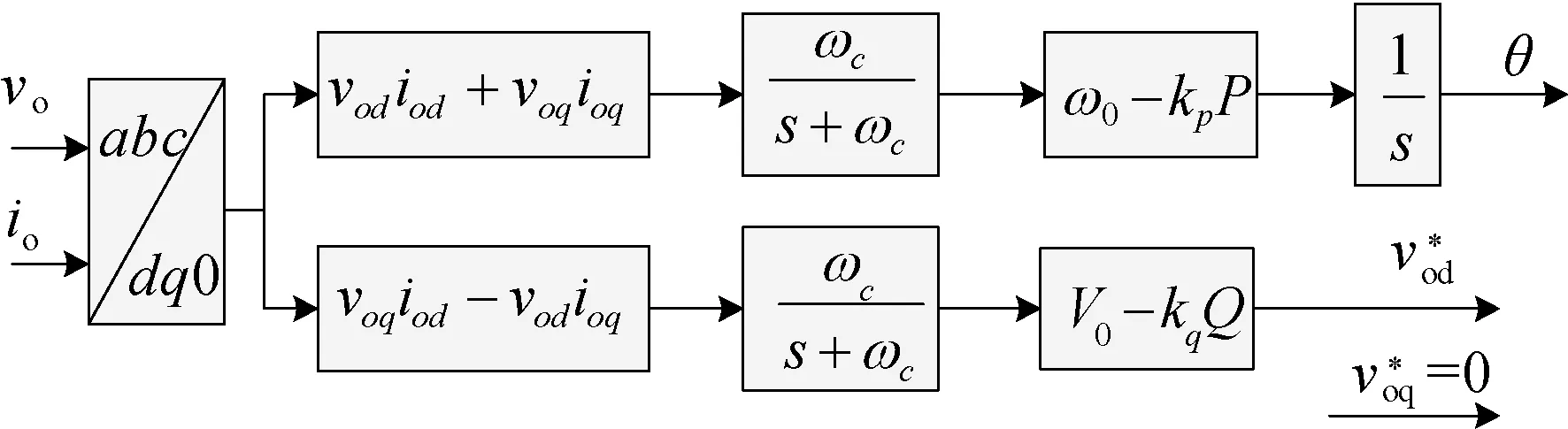
图3 功率控制器内部结构图Fig.3 Internal structure of power controller

图中经过dq0变换的vo，io变为四个分量，vod，voq，iod，ioq经过图中运算得到瞬时有功和无功功率，经过低通滤波环节得到平均功率，ωc是滤波器的截止频率，通常取为31.4 rad/s，对应的频率为5 Hz，时间常数为0.032 s，相比于电压控制和电流控制环节，此环节具有较大的时间常数，属于慢动态环节。

平均功率经过下垂曲线部分得到参考电压的幅值和频率，下垂系数的选取与逆变器的容量和要求的电压频率波动范围有关，通常情况下按下式确定：

式中：Pmax，Qmax分别为逆变器最大输出功率；ωmax，ωminvomax,vomin分别为系统允许的频率和电压最大最小值。

参考频率经过积分得到相位角，此相位角用于帕克变换的参考角度，一般情况下让电压参考值作输出电压d轴分量，令q轴分量为零，即实现输出电压的按d轴定向。

2.2 电压控制器和电流控制器的结构

为完整体现电压控制器和电流控制器的控制原理和结构，本文画出了包括逆变器开环部分在内的完整控制框图，如图4所示。

图4 逆变器电压电流控制器控制原理图Fig.4 Control principle diagram of inverter voltage and current controller

图中介于d轴分量与q轴分量之间的交叉项是为了抵消由abc坐标系变换到dq0坐标系时出现的耦合量而引入的，即所谓的前馈解耦，这样做可以将一个两输入两输出的耦合系统解耦成两个单输入单输出的系统，简化控制规律的设计。

图中电流控制器与开环部分之间实际上省略了逆变器本身的动态过程，由于用于与调制波比较的载波频率一般在6 000～8 000 Hz，逆变器开关频率很高，通常情况下可以忽略逆变器本身的动态效应。

如此一来，电流控制环的前馈解耦部分与系统开环部分由于dq0变换而出现的耦合量正好抵消，电流控制环作用到逆变器系统之后的等效框图如图5所示。

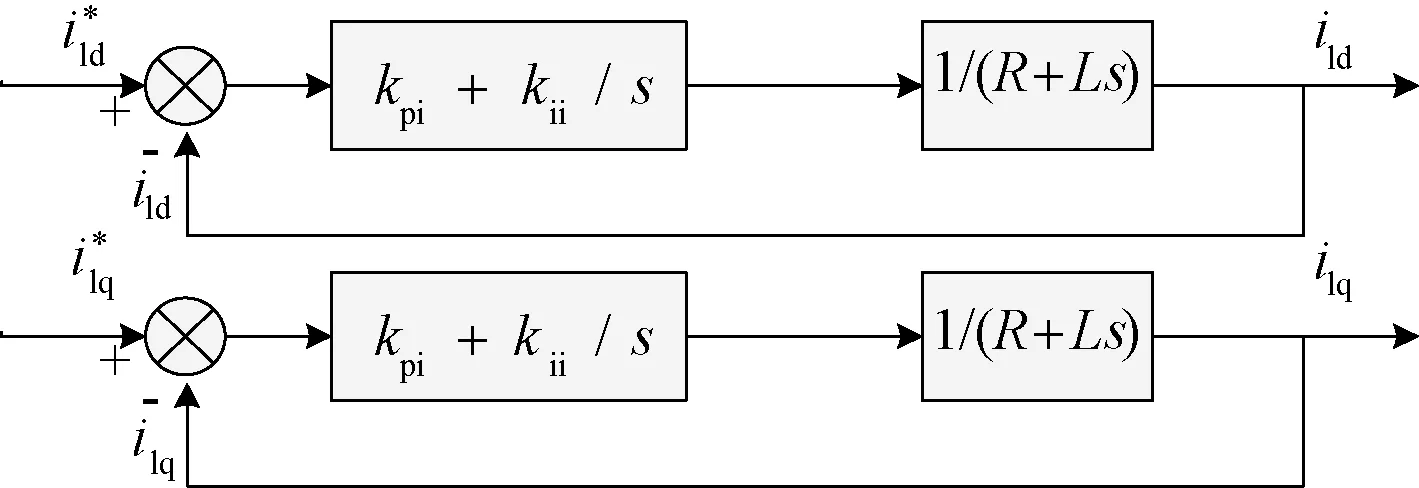
图5 电流控制器解耦后控制框图Fig.5 Control block diagram after decoupling of current controller

可以看出d轴与q轴分量实现了解耦，按照控制系统的设计方法，合理设计电流控制器的比例系数kpi和积分系数kii，可以得到满足系统要求的电感电流动态过程指针。

由于电流控制器处在电压控制器的内部，所以电流控制器又叫内环控制器，电压控制器又叫外环控制器。在内环控制实现解耦之后，电压控制器作用在逆变器系统上的等效框图变成图6所示。

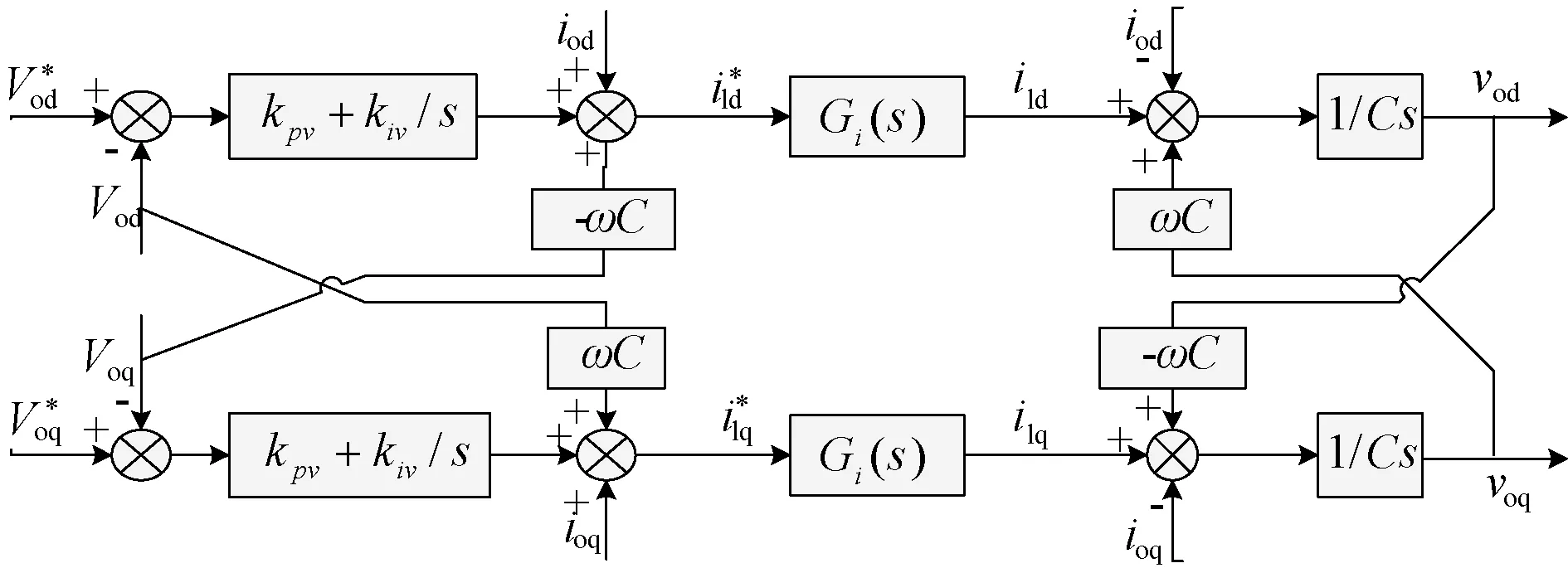
图6 解耦后电压控制器控制框图Fig.6 Control block diagram of voltage controller after decoupling

可以看出，从整个系统的角度来说，图所示的控制结构并没有实现真正意义上的电压解耦，因为电压控制器是经过电流控制环作用于开环系统的，只有在电流控制环的传递函数是1的情况下电压控制才达到完全解耦，这在实际系统中是不可能做到的。通常的做法是将电流控制环的带宽设计得很大，尽量减小电流控制环的动态过程对电压控制的影响。在文献[10]中作者设计的电流控制器带宽为1 600 Hz，电压控制器的带宽为400 Hz，按照控制理论的知识[11，12]，电流控制器的动态响应要比电压控制器快4倍，所以可以近似认为实现了解耦。

3 下垂控制的设计与仿真

3.1 功率控制器设计

图1中的功率控制器主要分为功率计算部分与功率滤波部分。功率计算部分采用dq0坐标系下的瞬时功率形式，对于功率低通滤波环节，一般选择低通滤波器的截止频率为电网额定频率的十分之一，这样通过滤波器的是变化缓慢的平均有功功率和平均无功功率。如果电网角频率为314 rad/s，则低通滤波器的截止频率ωc为31.4 rad/s。功率控制器的数学形式如图7所示。

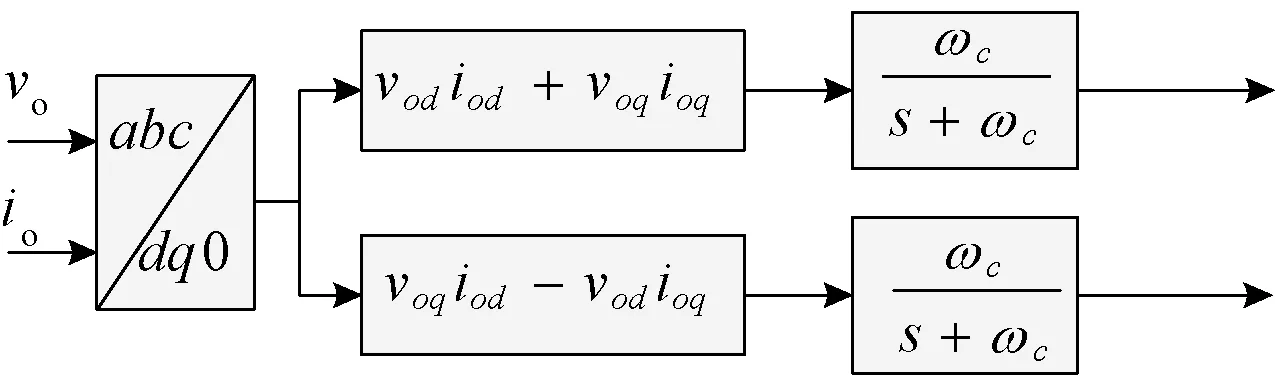
图7 功率控制器的数学形式Fig.7 Mathematical form of power controller

3.2 下垂系数的选择

下垂系数的选择应保证各逆变型电源在负荷变化后分担的功率变化量与其自身额定功率成比例，即满足：m1P01=m2P02=m3P03=…mnPn，当有功频率下垂系数取值不同时，各逆变型电源承担的负荷功率变化如图8所示：

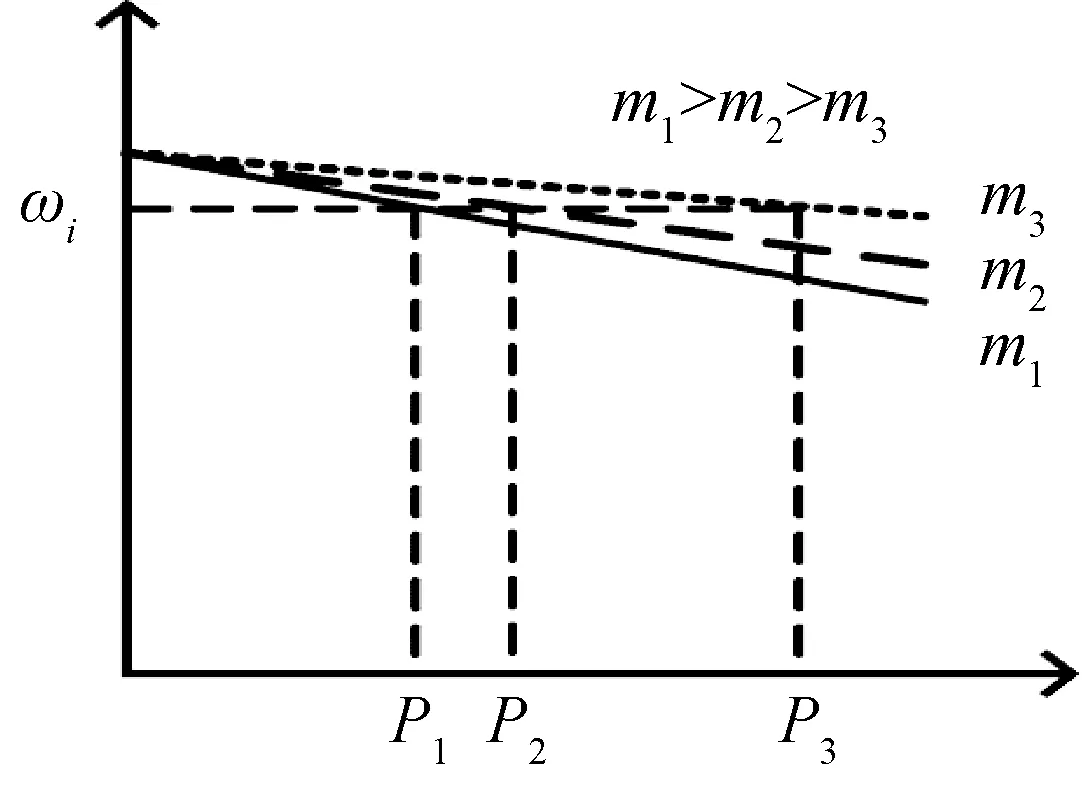
图8 不同有功频率下垂系数的功率变化情况Fig.8 Power variation of droop coefficient of different active power

可以看出，对应额定容量大的逆变电源在平衡负荷变动时承担较大的功率变动量。对于一个具体的逆变电源，其下垂系数的取值可以按下式确定：

(3)

(4)

式中：Pmax，Qmax为逆变器最大输出功率；ωmax，ωmin，vomax，vomin为系统允许的频率和电压最大最小值。

3.3 滤波器设计

采用正弦波脉宽调制技术(SPWM)时，在负载与逆变器直接输出端之间加输出滤波器起到接口作用，使得逆变出来的电压可以满足负载或者后续系统联接的要求，同时这个滤波器也是闭环控制系统得以控制逆变器输出电压的一个桥梁和通道。

LC滤波器一相的结构如图9所示。

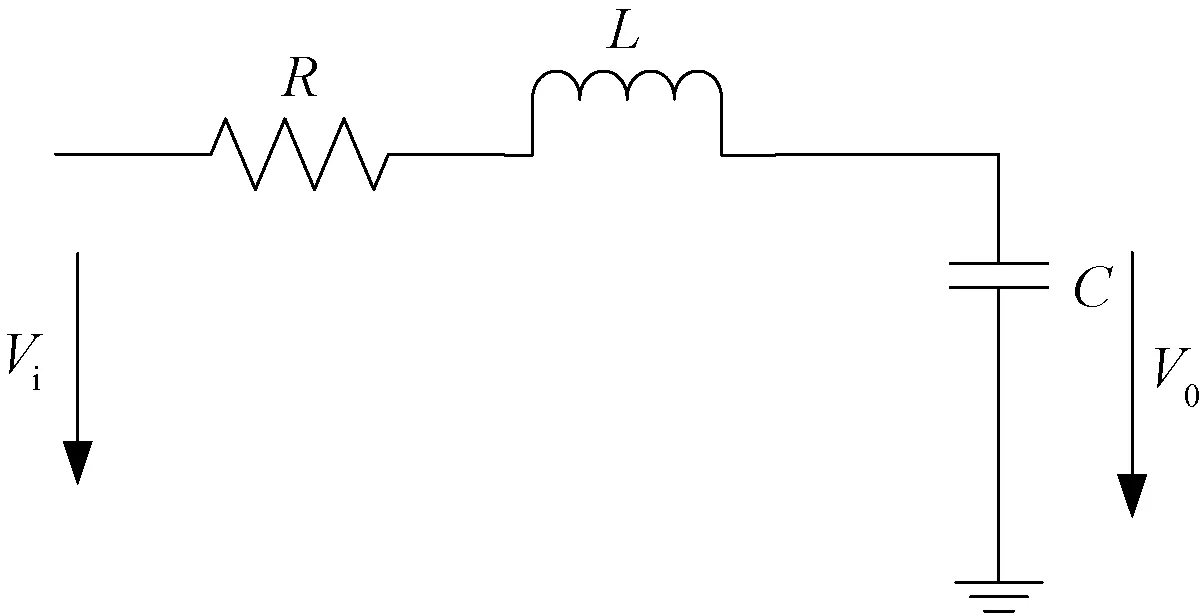
图9 LC滤波器单相的结构Fig.9 Single phase structure of LC filter

图中R代表电感的内电阻；L代表电感；C表示电容。

以Vi作为输入，Vo作为输出的传递函数为

(5)

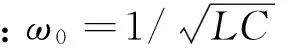
实际工程中确定ω0的一般原则是使其满足：

10fn≤f0≤fs/10，f0=ω0/2π

式中：fn为微网额定频率，fs为调制过程的载波频率。如果fs取6 000 Hz，fn为50 Hz的话，取滤波器参数为R=0.01 Ω，L=0.6 mH，C=1 500 μF，则可以得较好的滤波效果，通过仿真可以验证滤波器的效果显著。

3.4 载波频率的选择及逆变器本身的动态效应

在逆变器的控制过程中，三相逆变器的6个开关管IGBT的控制脉冲是由三角形载波与调制波幅值进行比较后得到的[13]，本文选择三角载波的频率fs=6 000 Hz；这既不会使逆变出的PWM波总谐波失真率过小，也不会增加管子的开关损耗，也不会使逆变出的PWM波总谐波失真率过大，给滤波系统造成负担。

3.5 电压电流双环控制的设计

3.5.1 电流环的设计

内环电流环通过前馈补偿实现解耦后，d轴与q轴分量可以单独控制，其中d轴电流的传递关系如图10所示。

图10 等效电流环的结构Fig.10 Structure of equivalent current loop

该系统的开环传递函数为

(6)

由此可以看出当电流环采用比例积分控制时，电流调节器是一个Ⅰ型系统，可以实现阶跃信号的稳态无误差跟踪。

闭环传递函数为

(7)

上两式中kpi，kii分别为为电流调节器的比例和积分系数。

由闭环传递函数看出，电流环是一个具有零点的二阶系统，只要kpi>-R,kii>0，闭环系统即可保证稳定，但两个变量变化的自由度较大，可以从系统的频率域出发进行设计解决，如果设计电流环的闭环系统的带宽频率ωb为1 600 Hz，则由带宽频率的定义有以下方程：

(8)

当滤波器参数取R=0.01 Ω，L=0.6 mH时，满足以上方程的kpi，kii取值如表1所示。

表1 kpi, kii取值表

由表格可以看出，积分系数kii的取值并不敏感，如果取kpi=6.041，kii=10，利用matlab软件绘出闭环系统的对数频率特性曲线和闭环系统的阶跃响应曲线，可得闭环系统的带宽越宽，则响应速度越快的结论，当ωb为1 600 Hz，可以得阶跃响应的上升时间约为0.2 ms。

3.5.2 电压环的设计

不计电流内环的动态效应，电压环的传递关系如图11所示：

图11 不计电流环的电压环传递关系Fig.11 Relationship between voltage loop and current loop

同样，其开环和闭环传递函数分别为

(9)

(10)

式中：kpv，kiv为电压调节器的比例系数和积分系数。

仿照电流环的设计方法，如果令电压环的闭环系统带宽为400 Hz，则可得到满足要求的调节参数取值为：kpv=3.766，kiv=10。利用matlab绘出电压环的闭环频率特性和阶跃响应曲线可以得出上升时间约为0.8 ms。

由于所设计动态指标也只是针对dq0坐标系内阶跃信号输入引起的响应，借助文献[14]的变换方法可以得到等效到ABC坐标系的输入电压与输出电压的关系，A相与B相之间具有耦合关系。

3.6 下垂控制在不同运行方式下的仿真

仿真所用模型如图12所示，其中包含三个微源，DG1和DG2采用本文设计的下垂控制，DG3采用恒功率控制(PQ)，且都带有其本地负荷，并通过公共母线和公共点耦合开关PCC与大电网相连，公共母线上还有一个公共负荷，模拟负荷变化，来考察控制策略在负荷变化时的工作效果。

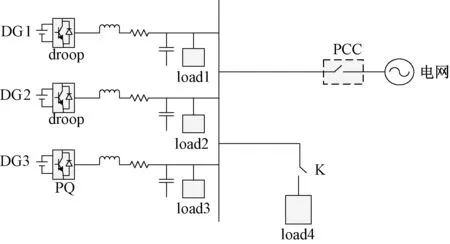
图12 仿真模型图Fig.12 Simulation model diagram

3.6.1 离网运行时下垂控制的仿真

离网运行仿真时仿真模型中PCC断开，负荷投切开关打开，仿真时间设为1.5 s，假定0.5 s时刻三个带有本地负荷的微源均已达到稳定运行状态，0.5 s时闭合负荷开关，得如图13所示仿真结果。

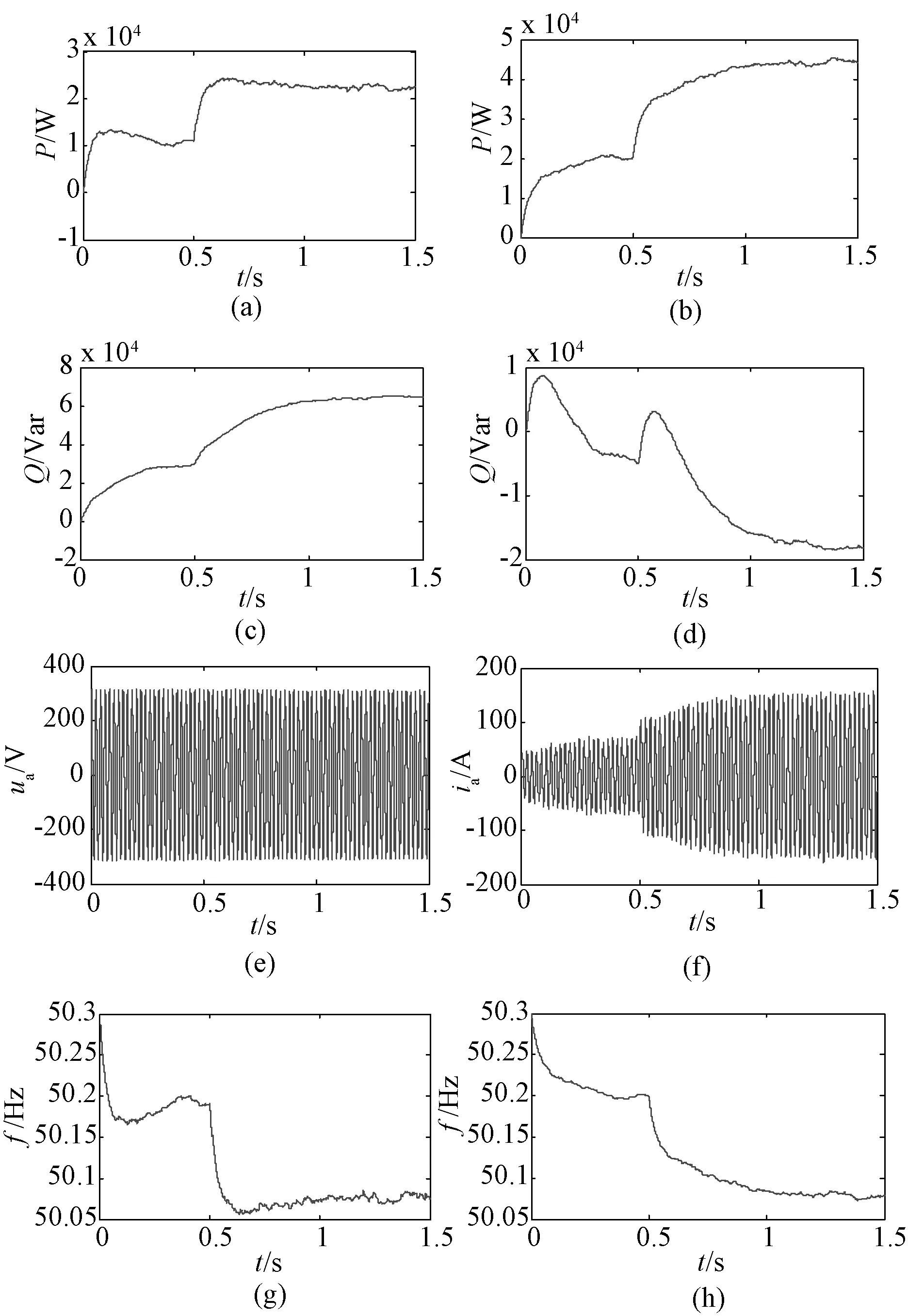
图13 离网运行时的仿真结果Fig.13 The simulation results

图(a)与图(b)是两个采用下垂控制的微源DG1和DG2有功功率变化的曲线，负荷增加时，两个微源增大了有功出力，且幅度与额定容量成比例；图(c)与图(d)是DG1与DG2无功功率变化曲线，DG2的发出无功功率为负值，说明两个逆变电源之间存在环流，这是两逆变器的参数不完全对称造成的，实际应用中，应避免此类环流，否则会造成电源容量浪费；图(e)与图(f)是DG1输出A相电压与电流变化曲线，负荷增加，输出电压幅值变化不明显，输出电流增加明显；图(g)与图(h)是DG1与DG2频率变化曲线，下垂控制曲线方程在负荷增加后会降低输出电压频率，所以两微源的频率在负荷增加后都有所降低，达到稳态则具有相同频率。

以上描述说明，离网运行时设计的下垂控制基本能满足微网系统的要求，下垂控制不借助通信线实现逆变电源之间的功率共享在一定条件下可以实现，但因为电压变量并不能像频率在达到稳态后系统处处相等，无功功率得不到很好的控制，所以这种控制策略只是侧重于有功功率在逆变电源之间的分配。

3.6.2 联网运行时的仿真

仿真模型中PCC闭合，负荷投切开关在开始处于打开状态，仿真时间设为2 s，假定1 s时刻三个微源与电网组成的系统已达稳定运行状态，1 s时闭合负荷开关，得如图14所示的仿真结果。

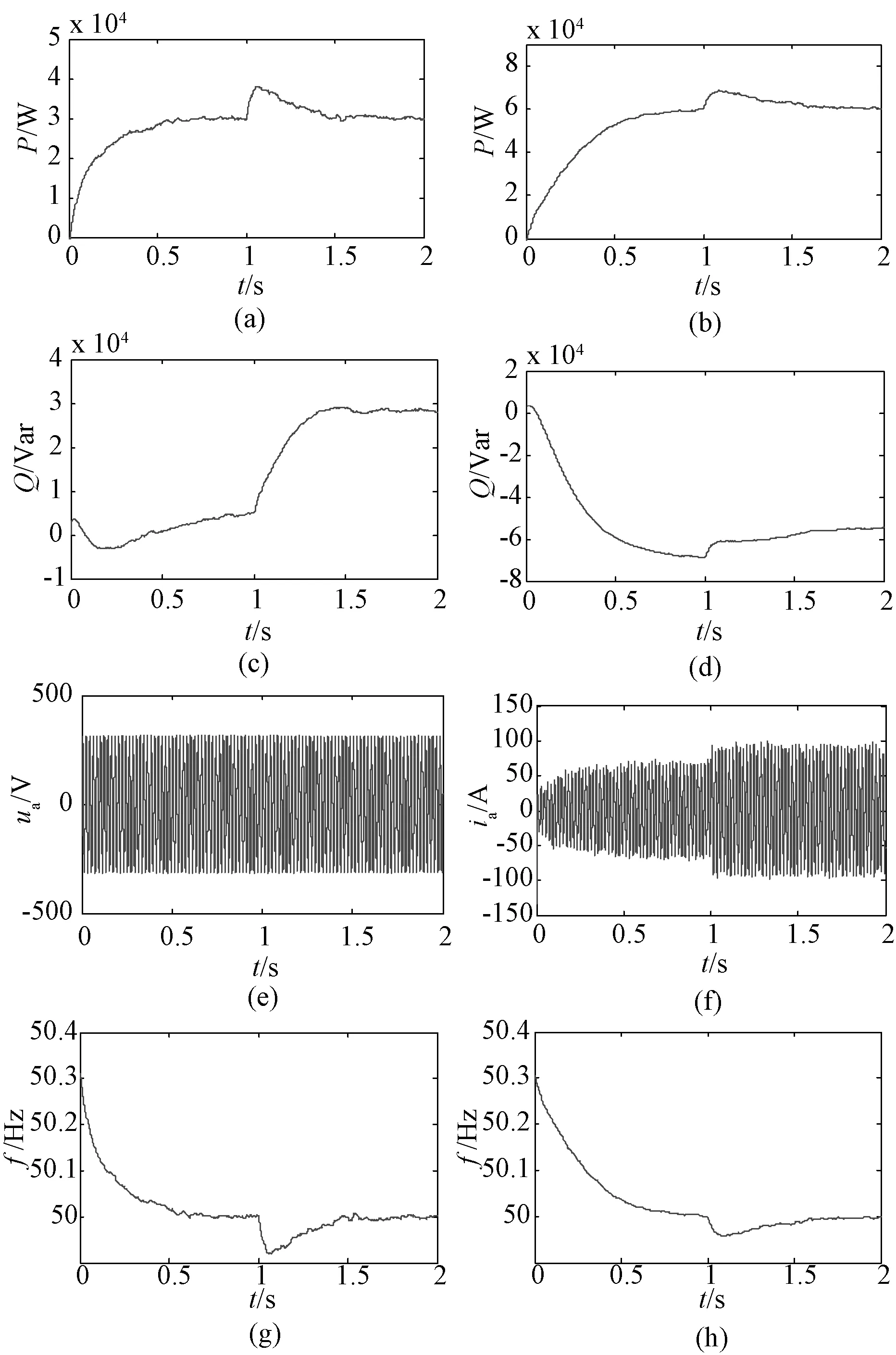
图14 联网运行时的仿真结果Fig.14 Simulation results of network operation

图(a)与图(b)为DG1和DG2有功功率变化曲线， DG1与DG2在负荷增加前后有功功率维持不变；图(c)与图(d)为DG1和DG2无功功率变化曲线， DG1发出无功变化大，DG2发出的无功变化小，可以看出负荷的增加对DG2的影响不大，而主要反映在电网和DG1之间，有功功率增加全部由电网承担，无功功率增加由电网和DG1共同承担，这再次说明了传统下垂控制对无功功率的控制乏力；图(e)与图(f)为DG1输出A相电压和电流变化波形，电流幅值在负荷增加后变大，反映DG1输出无功增加；图(g)与图(h)是两微源在负荷增加前后频率波形，由于联网运行，达到稳态后二者的频率都是电网频率50 Hz。

3.7 离网运行时下垂控制的频率恢复

离网运行时下垂控制是逆变型微源输出电压频率随着负荷的增加而减小，反之则使系统频率偏离额定值过大，不满足负荷用电的要求，这时需要考虑离网运行时下垂控制的频率恢复办法。

离网运行时下垂控制的有功频率特性改进如图15所示。

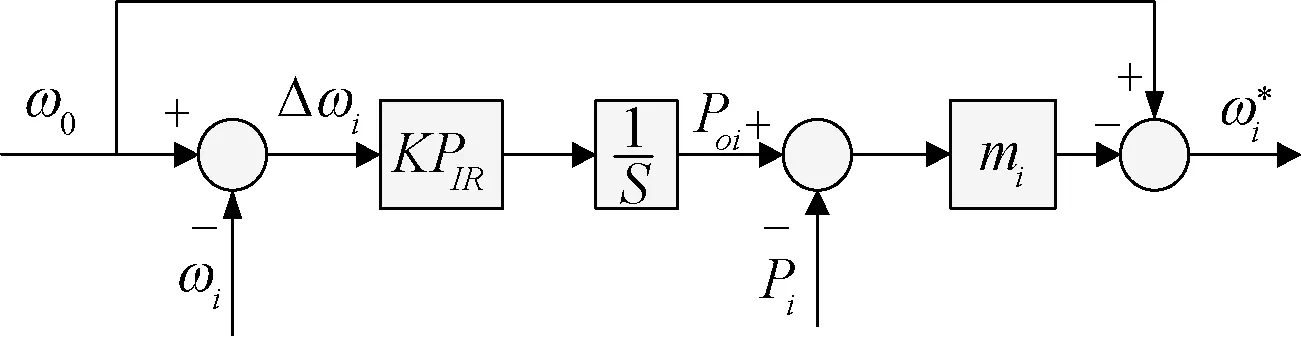
图15 离网时改进有功频率下垂特性Fig.15 Improved active frequency droop characteristic when off grid

图中PIR是逆变器额定功率，K是影响频率调节速度的比例因子。原固定不变的P0i变为受频率偏差Δωi影响的变量，由于前向通道中有一个积分环节，使得微网系统进入稳态后，系统频率ωi与额定频率ω0偏差Δωi为零。该过程中，P0i的值不断改变，调节过程中仍可以保证微源按比例分担负荷。实际上，改变P0i使离网系统频率恢复额定值的过程相当于传统电力系统的二次调频过程，此改进相当于为微网系统增加了调频器，而传统下垂控制却只能进行一次调频。

图16为DG1和DG2在改进下垂控制下的仿真曲线，稳态后系统频率得以恢复到额定值，也保证了两微源按比例分担增加的负荷，验证了所提策略的有效性。

图16 离网时改进有功频率下垂特性仿真曲线Fig.16 Simulation curve of improved active frequency droop characteristic

4 结 论

本文研究了微网中采用下垂控制的逆变器与配电网并网运行时的特性。首先通过结构图对下垂控制的调节原理作了分析，接着对下垂控制各个功能模块的实现作了介绍，重点介绍了电压电流控制器的实现原理，接着进行了下垂控制各个环节的设计，其中包括功率控制器设计，下垂系数选择，滤波器设计，电压电流双环控制参数设计等，并对下垂控制器在微网联网和离网两种运行方式下的控制效果进行仿真并得出结论：下垂控制策略可以控制有功功率在各逆变电源之间的按比例分配，但电源发出无功功率主要受网络结构和线路参数影响，单纯依靠下垂控制调节，并不能实现无功功率在各电源之间按比例合理分布，因此对实际运行的微电网，保证经济有功损耗最小，实现无功潮流的优化分布，应考虑控制无功分布的问题，最后对离网运行重负荷时的频率恢复问题做了研究，设计了微网频率恢复控制结构，并通过仿真验证了所提策略的有效性。

[1] 杨新法,苏剑,吕志鹏,等. 微电网技术综述[J]. 中国电机工程学报,2014,34(1)：57-70.

[2] 艾欣,邓玉辉,黎金英. 微电网分布式电源的主从控制策略[J]. 华北电力大学学报(自然科学版),2015,42(1)：1-6.

[3] 张建华,苏玲,刘若溪，等. 逆变型分布式电源微网小信号稳定性动态建模分析[J]. 电力系统自动化, 2010, 34(22): 97-100.

[4] COELHO E A A, CORTIZO P C, GARCIA P F D. Small signal stability for single phase inverter connected to stiff ac system[C]// Thirty-Fourth IAS Annual Meeting, Conference Record of the 1999 IEEE, 03 Oct 1999-07 Oct 1999, Phoenix, AZ, America: 2180-2187.

[5] 李洋,张辉,苏冰,等. 含多微源的微电网离网运行小信号稳定性分析[J]. 电力自动化设备,2015,35(1):159-164.

[6] COELHO E A A, CORTIZO P C, GARCIA P F. Small-signal stability for parallel-connected inverters in stand-alone AC supply systems[J]. Industry Applications, IEEE Transactions on, 2002, 38(2): 533-542.

[7] RYAN M J， LORENZ R D. A high performance sine wave inverter controller with capacitor current feedback and back-emf decoupling[C]// Power Electronics Specialists Conference, 18-22 Jun 1995, Atlanta, GA: 507-513.

[8] 张建华,苏玲,刘若溪，等. 逆变型分布式电源微网并网小信号稳定性分析[J]. 电力系统自动化, 2011, 35(6): 76-80.

[9] ANDRADE F, CUSIDLJ, ROMERAL L. Transient stability analysis of inverter-interfaced distributed generators in a microgrid system[C]// Proceedings of the 2011-14th European Conference, Aug. 30 2011-Sept. 1 2011, Birmingham, UK: 1-10.

[10] POGAKU N， PRODANOVIC M， GREEN T C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid[J] Transactions on Power Electronics,2007,22(2):613-625.

[11] 胡寿松. 自动控制原理(第五版)[M]. 北京: 科学出版社, 2006.

[12] 李鹏,杨世旺,殷梓恒. 基于相对增益矩阵的微网稳压解耦下垂控制方法[J]. 中国电机工程学报,2015,35(5):1041-1050.

[13] 张庆海,彭楚武,陈燕东,等. 一种微电网多逆变器并联运行控制策略[J]. 中国电机工程学报,2012,32(25):126-132.

[14] ZMOOD D N， HOLMES D G， BODE G H. Frequency-domain analysis of three-phase linear current regulators[J]. IEEE Transactions on in Industry Applications, 2001,37(2):601-610.

Double Closed Loop Droop Control Method and Design for Inverter of Voltage and Current in Micro-grid indq0 Coordinate System

LI Yanqing, WANG Zirui

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003,China)

The droop control is one of the widely used control strategies in micro-grid. When droop-control inverter operates with connection to the grid, the output power of micro-source equals to the power value of sagging curve with 50 Hz. The inverter acts as constant power output. This paper introduces the basic principle of droop control and the implementation method, also it studies the characteristics of droop-control inverter when it is connected to the distribution network, drawing the conclusion that line impedance and droop coefficient are the system damping during the process of grid connection. Parameter values of droop-control power controller and filter at the output inverter are determined. Simulation has been made for the design with Matlab, and control method of frequency recovery was proposed for droop-control with off-grid operation.

droop control; grid-connected operation; decoupling; double closed loop control; stability; frequency

10.3969/j.ISSN.1007-2691.2017.01.06

2016-04-22.

TM712

A

1007-2691(2017)01-0039-07

李燕青(1974-)，男，教授，研究方向为电网规划，新能源发电与微电网控制等;王子睿(1991-)，男，硕士研究生，研究方向为微电网控制策略与微网并网。