串联五个基本三角不等式的一条不等式链

福建省福清第三中学 (350315) 何 灯福建省福清东张中学 (350305) 王少光

串联五个基本三角不等式的一条不等式链

福建省福清第三中学 (350315) 何 灯福建省福清东张中学 (350305) 王少光

1．缘起

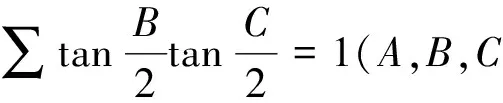
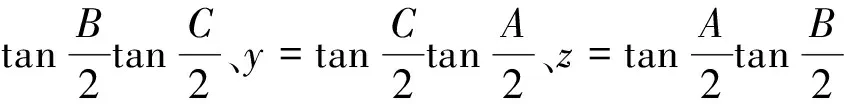
2．若干引理

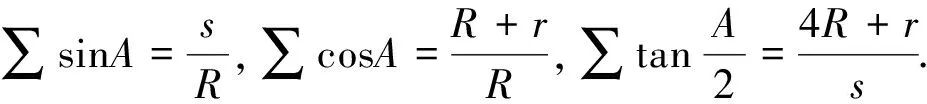
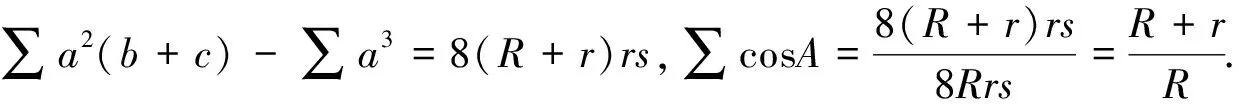
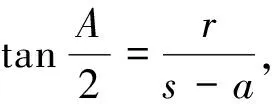
引理2 设ΔABC的三边为a,b,c，外接圆和内切圆半径分别为R,r，s为半周长，则有R≥2r(Euler不等式),16Rr-5r2≤s2≤4R2+4Rr+3r2(Gerrestsen不等式).

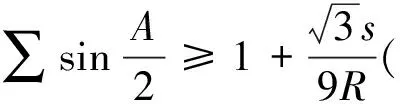
3．一条基本三角不等式链

定理 在ΔABC中，有

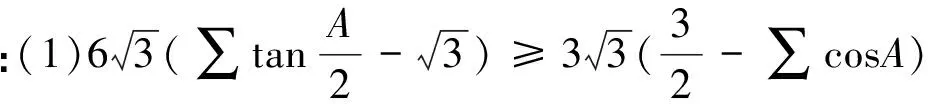
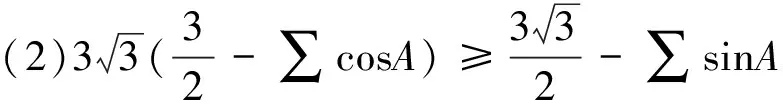
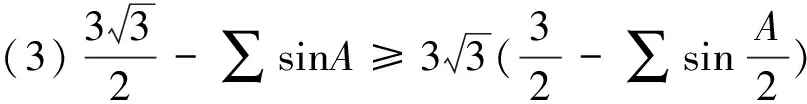
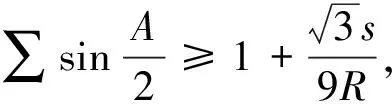
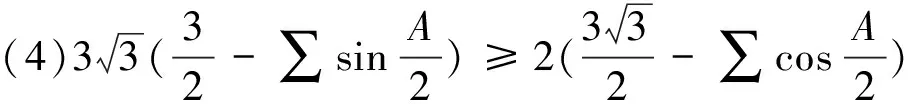
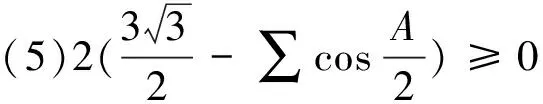
综上，定理成立.

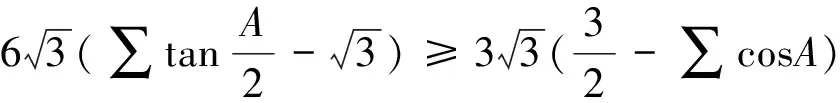
[1]程汉波.三角代换 巧证代数不等式[J],中学数学研究(广东),2014(3):38-39.

[2]查正开.一类代数问题的三角解法[J],中学教研(数学),2015(4):15-19.

[3]程汉波.三正数和为1条件不等式的换元证法[J],数学教学,2015(7):27-28.

[4]安振平,崔歧恩.由三角形不等式生成代数不等式的一种方法[J],数学通报,2010(8):48-50.

[5]张俊.一个三角形恒等式繁衍出的代数不等式[J],数学通讯(下半月),2010(9):61-62.

[6]程汉波,杨春波.简单三角不等式引致的优美代数不等式[J],数学通讯(下半月),2013(3):41-43.

[7]程汉波.再议简单三角不等式引致的优美代数不等式——从重要三角恒等式的视角[J],数学通讯(下半月),2014(10):52-55.

[8]杨学枝,尹华焱.我国研究三角形中半角三角函数不等式情况综述[A],杨学枝,不等式研究(第一辑)[C],西藏:西藏人民出版社,2000,6.

[9]安振平.二十六个优美的不等式[J],中学数学教学参考(上旬),2010(1-2):136-143.