例谈平面向量中几种解题技巧

广东省惠州市第一中学 (516007) 方志平

例谈平面向量中几种解题技巧

广东省惠州市第一中学 (516007) 方志平

由于平面向量融数、形于一体，它既有一套良好的代数运算法则，又有直观形象的图形特征，因而使得平面向量成为研究数与形的一种有效工具，其思想方法独树一帜，内涵深邃.又因为平面向量问题的灵活多变，所以很多中学生在学习时觉得困难较大，甚至感到无从下手.基于这些本文借用一些典例浅谈平面向量中几种解题技巧，供同学们学习参考.

1.利用向量的分解与合成解题

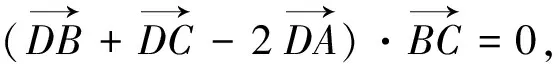
A. 直角三角形B. 等腰三角形

C.等腰直角三角形D.等边三角形

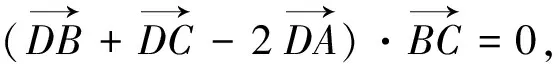
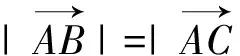
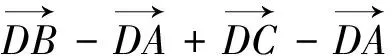
2.引用向量的坐标运算解题

A．13B．15C．19D．21

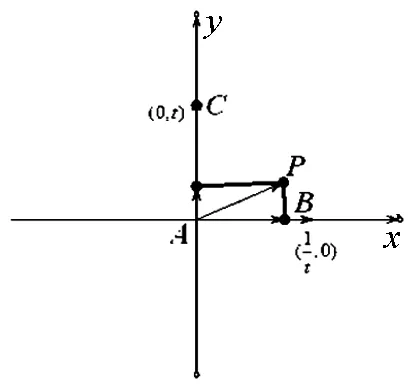
图1

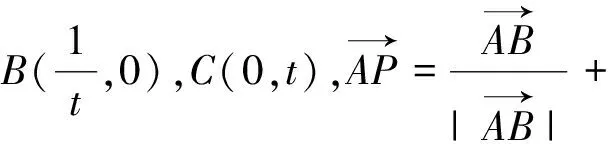
点评：这里引用了向量的坐标思想，即用向量的坐标来揭示二维平面上几何元素的属性和彼此间的关系，将条件和结论有机的联系起来.向量的坐标是将几何问题用代数手段来解决的重要工具，同时，坐标的运用极大地方便了计算和论证.

3.巧用向量的一组基底解题

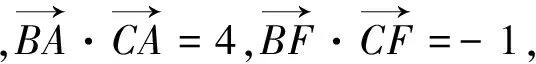
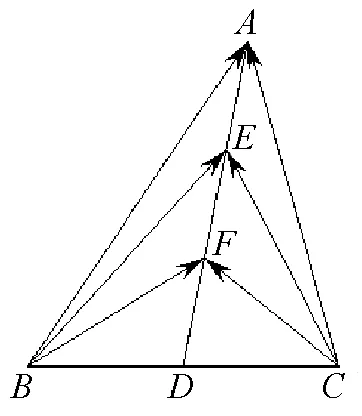
图2

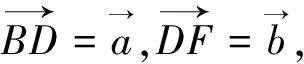
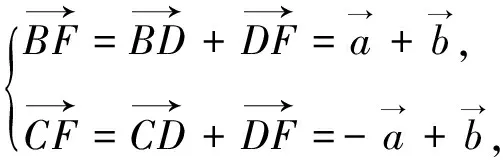
4.使用三点共线解题

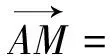
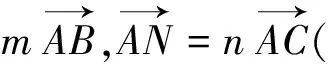
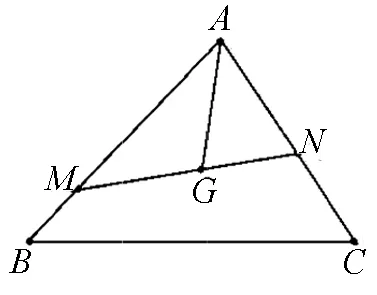
图3

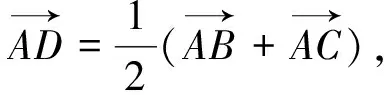
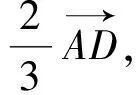
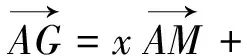
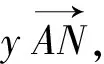
5.妙用向量实数化解题

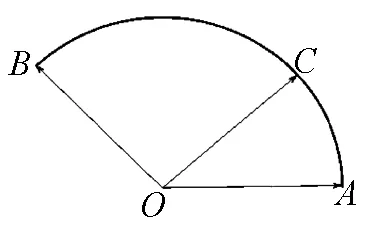
图4

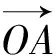
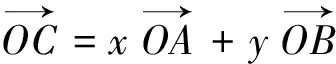
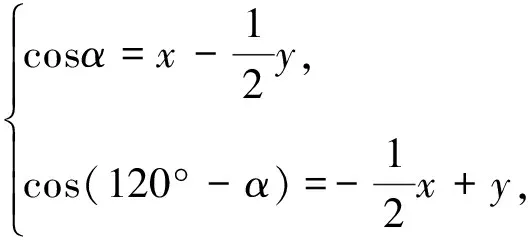
6.构造图形解题

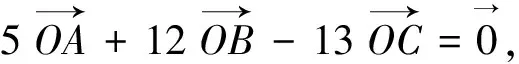
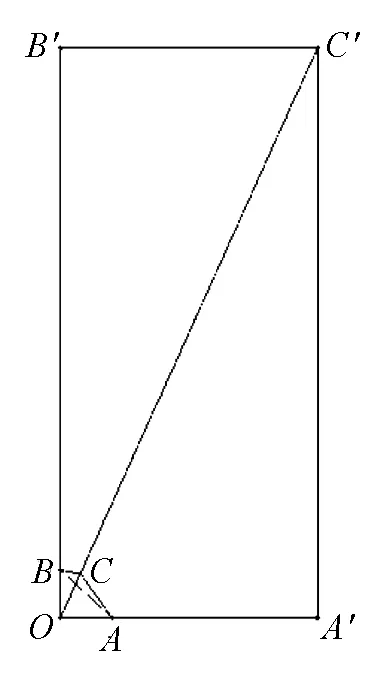
图5

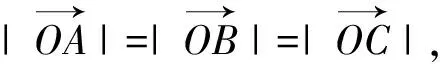
点评：由于向量兼具代数和几何的诸多特性,使之成为沟通数与形的枢纽,本题正是根据这一特点，结合题设条件构造特殊图形进行求解.

7.活用向量的数量积变形公式解题

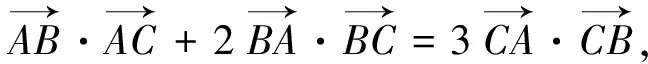
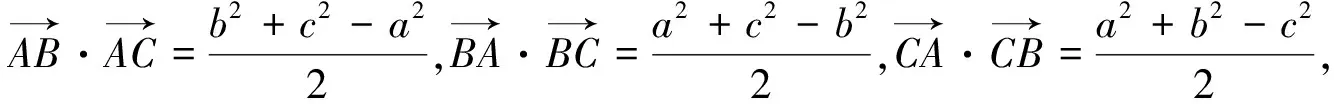
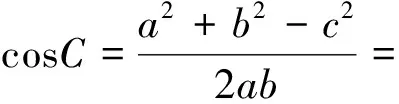
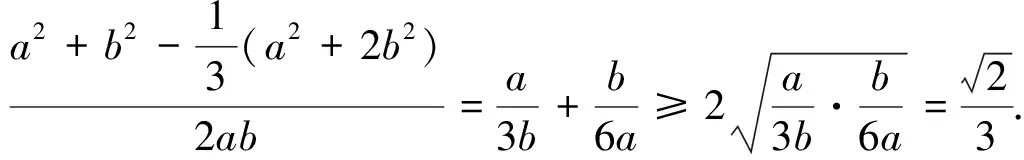
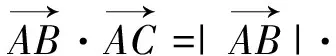
8.运用向量的平行关系解题

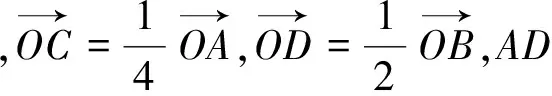
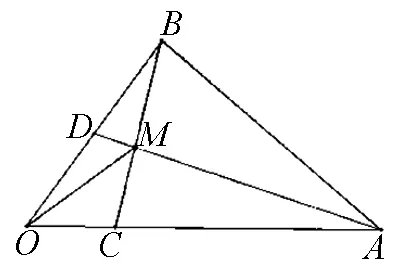
图6

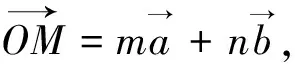
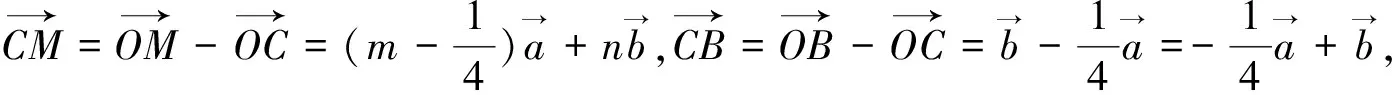
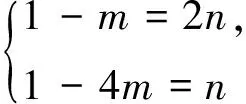
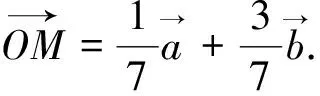
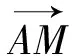
9.采用向量的垂直关系解题

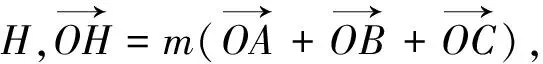
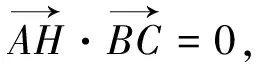
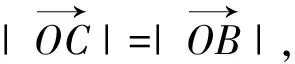
点评：由于本题是一道填空题，故也可使用特殊值法求解，即ΔABC可视为等腰直角三角形，则O是斜边AB的中点，垂心H是直角顶点.也很容易得出答案.另外，一般处理涉及向量垂直问题的常用方法是利用向量数量积等于零或建立直角坐标系转化为平面向量的坐标运算.

综上，平面向量是现代数学中的一个新生内容，它的引入给中学数学带来了无限的生机，也给中学数学教与学带来了挑战.近些年来高中各类考试出现了不少以平面向量为载体的选择题或填空题，这类问题“小巧玲珑”，内容丰富，方法灵活，具有一定的综合性.上述例析的仅是平面向量解题技巧中的冰山一角，本文旨在起抛砖引玉作用，期望读者能够触类旁通.