数学竞赛中的高斯函数

广东省兴宁市宁中中学 (514500) 刘继东

数学竞赛中的高斯函数

广东省兴宁市宁中中学 (514500) 刘继东

在各级各类的数学竞赛中经常出现高斯函数的试题，本文例举高斯函数在数学竞赛中一些应用.

1.解方程

解含[x]的方程，常利用[x]的性质、采用变量代换等方法将方程转化为不等式，通过解不等式求出原方程的解.

例1 (2015天津)用[x]表示不大于x的最大整数，方程x2-[x]-2=0共有( )个不同的实根.

A.1B.2C.3D.4

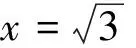
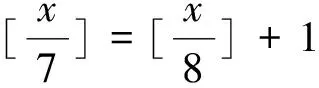
2.求值

[x]的求值问题，可先确定x的取值范围，再求[x]的值，也可先利用代数变形，再利用高斯函数的性质求值.

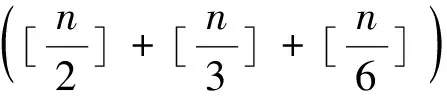
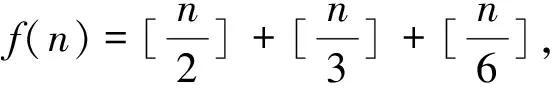
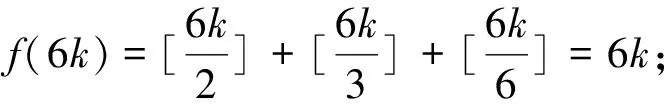
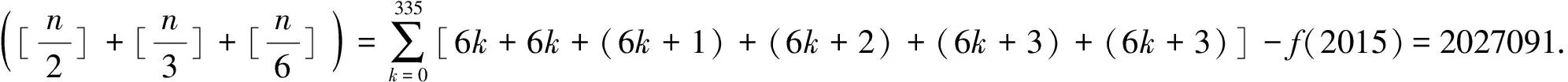
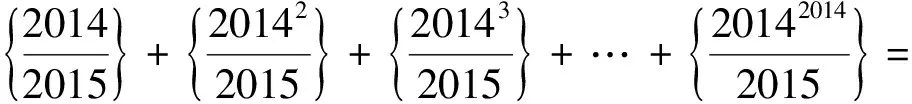
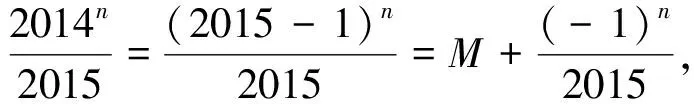
3.平面区域与高斯函数

曲线中含高斯函数，常用方法是分类讨论，将曲线分成几部分来考虑.

例5 (2016浙江)记[x]为不超过x的最大整数.若集合S={(x,y)||[x+y]|+|[x-y]|≤1}，则集合S所表示的平面区域的面积为( ).

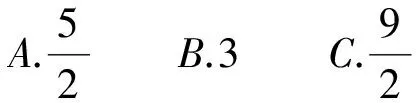
解:当0≤x+y<1时，[x+y]=0，∴|[x-y]|≤1，即-1≤x-y<2；当1≤x+y<2时，[x+y]=1，所以|[x-y]|=0，即0≤x-y<1；当-1≤x+y<0时，[x+y]=-1，所以

|[x-y]|=0，即0≤x-y<1.

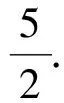
4.数列与高斯函数

数列中的核心问题是求通项与求和，求通项的方法有累加法、累乘法、构造法等，而求和的方法有并项求和、分组转化、错位相减、倒序相加、裂项相消等.在解数列与高斯函数这类问题时，这些方法要与高斯函数的定义和性质相结合.

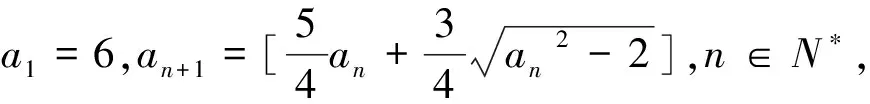
A.1B.2C.5D.6

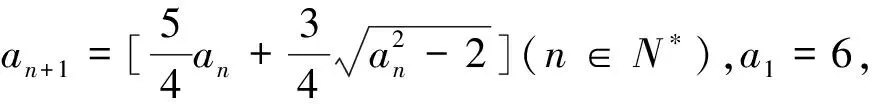
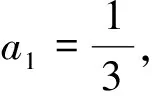
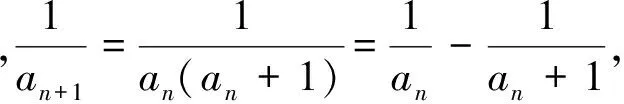
5.个数问题

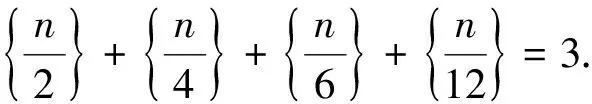
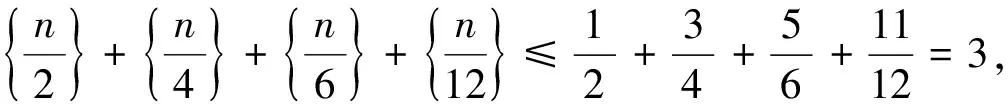
例9 (2016安徽)集合{[x]+[2x]+[3x]|x∈R}∩{1,2,…,100}共有 个元素，其中[x]表示不超过x的最大整数.

解:设f(x)=[x]+[2x]+[3x]，则有f(x+1)=f(x)+6，当0≤x<1时，f(x)的所有可能值为0,1,2,3.由此f(x)值域S={6k,6k+1,6k+2,6k+3|k∈Z}，S∩{1,2,…,100}共有4×17-1=67个元素.

6.同余问题