穷举法在确定带电粒子在磁场中轨迹的应用

吴文肖

摘 要： 关于带电粒子在磁场中的处理问题，除了必要的半径及时间推导公式外，有效确定粒子的圆弧轨迹显得尤为关键。区别于传统“定圆心”“取半径”“画圆弧”的常规法，本文从另一个角度给出了一种确定粒子轨迹的新方法——“穷举法”，通过这种方法在例题中的实践应用，让读者通过不断作圆的过程体验粒子的运动特点，达到对粒子的动力学认识以及物理数学综合能力的双重提升。

关键词：穷举法；应用；讨论

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2017）2-0036-3

帶电粒子在磁场中运动，往往会受到洛伦兹力而做匀速圆周运动。确定粒子的运动轨迹成为解决其相关物理问题的核心。现行高中教材主要是利用粒子运动的几何特点来加以确定，但是这种方法在原理特点上，带有较为明显的几何特征，对几何数学的知识储备要求较高，对多粒子或多轨迹的复杂运动处理起来则显得力有未逮。那么，有没有一种更接近物理学科特点，更优化，更能被学生接受同时提升其发展能力的处理方法呢？下面我们将介绍一种全新的方法，并对这种方法的应用功能加以讨论。

下面我们认识一下粒子运动的两个重要特点：

1 两点认识

1.1 半径推导式

带电粒子在洛伦兹力作用下做匀速圆周运动，洛伦兹力提供向心力，运行的半径推导：r=。因此，对于同一带电粒子的运动，入射速度越大，磁场越弱，粒子运动的圆周半径越大。

1.2 运动时间推导式

由粒子的周期公式可推导运行的时间：t=。可见，对于同一带电粒子的运动，圆弧对应的圆心角越大，磁场越弱，运行时间越久。

2 穷举法

2.1 基本思想

穷举思想属于数学和计算学范畴的分支，广泛应用于数学高端难题及密码破译工作中，是一种针对不定或难定事件，通过给出可能满足的系列假设解，再通过筛选对这些解进行一一验证，从而取出满足题设所有条件的唯一解的方法。[1]

2.2 基本原理

带电粒子在磁场中的运动轨迹的确定，实际上就是一个寻找唯一解的过程。常规法中利用垂径定理和一条垂直于速度的线或两条分别垂直于速度的线的交点来“定圆心”。但是，对于运动轨迹的不确定性、多解性或模糊性所导致的运动轨迹难定的物理模型，常规法的应用就显得捉襟见肘了。对此，我们急需一种优化方法有效解决这类问题。

穷举法的步骤：（1）根据洛伦兹力的方向确定圆心的大致范围；（2）在圆心范围内作系列圆弧轨迹；（3）筛选圆弧遴选出满足题意所有条件的圆弧。

3 应 用

粒子在匀强磁场中的轨迹的难定性主要来自入射速度大小的不确定性、磁感应强度大小的不确定性及入射方向的不确定性三个方面。而其中由入射速度大小及磁感应强度大小所导致的运动不定在效果上一致。下面分成两大类进行简要应用举例。

3.1 入射速度（或磁感应强度）大小不定

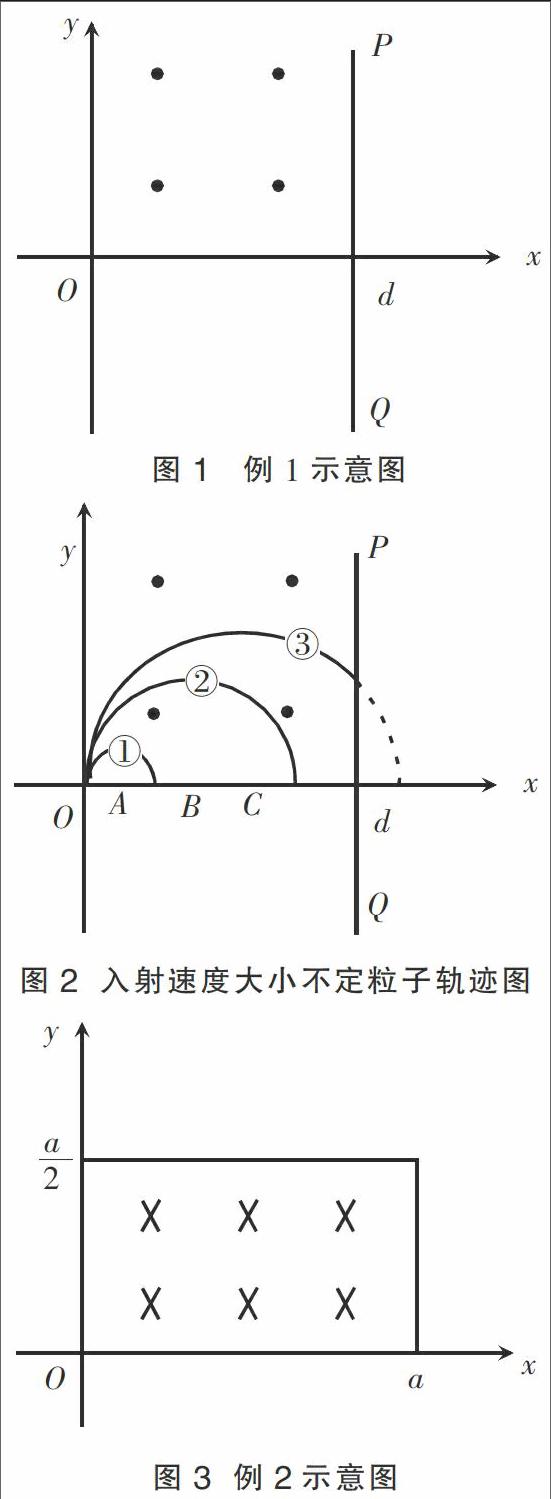
例1 已知xOy系第一象限内分布如图1所示的匀强磁场，磁场方向垂直于纸面向外，磁感应强度为B，距离原点d位置处竖直放置挡板PQ。某时刻从O点竖直向上入射一束质量为m，电荷量为q的正电粒子，粒子的速度大小各不相同，若要让所有粒子都能经过磁场最终打在挡板PQ上，试求粒子发射速度至少为多少？

解析 由于入射正电粒子速度方向始终竖直向上，洛伦兹力方向始终水平向左，即圆心应该分布在x轴正半轴区间内。入射速度大时，圆心分布较远；速度小时，圆心分布较近。若从左至右逐一取圆心A、B、C等，以OA、OB、OC等作系列圆弧①、圆弧②、圆弧③（如图2所示），其中“最近”圆弧①对应最小的入射速度，“最远”圆弧③对应最大的入射速度。

显然，要让所有粒子能打在挡板PQ上，只需要“最近”的圆弧①运动的粒子能够打在挡板上即可。

至少满足条件：r>。

由r=，易得：v>。

反思1 观察图2，若粒子全部打在挡板上，主要集中在PQ哪一端？（PQ“上半段”）

反思2 上题中，若要让所有粒子都不打在挡板PQ上，发射的速度又有什么要求？

（观察图2可得，要让粒子都不打在挡板上，要求“最远”的圆弧③不能打在挡板上，至少满足条件：r≤， 即v≤）

3.2 入射速度方向不定

例2 如图3所示，在0≤x≤a，0≤y≤范围内存在垂直于xOy平面向里的匀强磁场，磁感应强度为B。坐标原点O处有一个粒子源，某时刻发射大量质量为m、电荷量为q的负电粒子，它们的速度大小相同，速度方向均在xOy平面内，与y轴正方向夹角在0 °至90 °之间。已知粒子在磁场中做圆周运动的半径介于到a之间，从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中已知粒子在磁场中做圆周运动周期的四分之一。求最后离开磁场的粒子的速度大小？

解析 据题意知入射方向朝着第一象限任意方向，洛伦兹力的方向对应分布在第四象限。由于入射粒子的速度大小相等，粒子运动半径应该等大，即所有粒子的圆心分布在以介于半径到a之间距离作圆弧的四分之一圆弧AA'上；然后，在AA'范围内依次取点A、B、C等，以OA、OB、OC等作系列圆弧①、圆弧②、圆弧③（如图4所示），其中圆弧①对应竖直向上入射，圆弧②③对应逐渐偏向x轴入射。

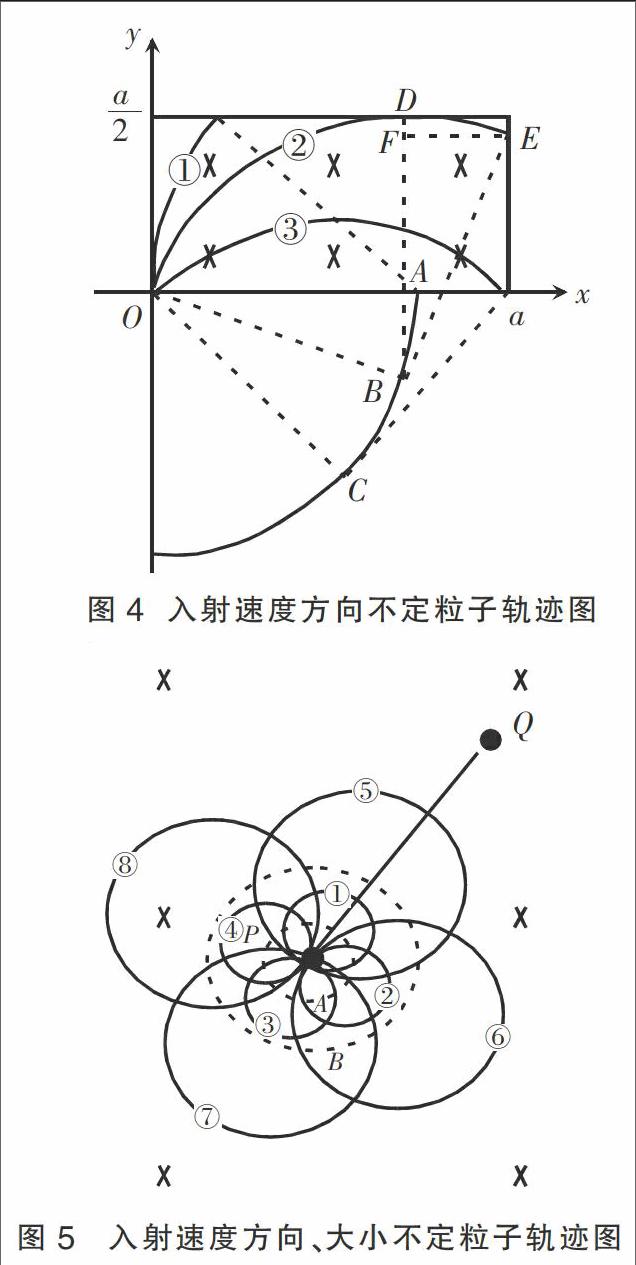
观察系列圆弧可知，圆弧①到圆弧②过程，粒子留在磁场中的轨迹逐渐变长，而圆弧②到圆弧③轨迹长度又逐渐变短。对于相同的运行速率，轨迹最长的圆弧②所对应的运行时间应该最长，轨迹长度为四分之一圆弧，圆心角为。设圆弧②交矩形上边于D，右侧边于E，连接BD，过E作线段，EF⊥BD。

反思3 观察图4，是否有粒子从坐标（a，0）射出？射出的方向是竖直向下？（有，不是竖直向下）

3.3 入射速度（或磁感应强度）大小及方向均不定

例3 如图5所示，垂直于纸面的匀强磁场，有一个电子源P，它向纸面的各个方向发射等速率的电子。已知电子质量为m，电荷量为e，纸面上PQ两点间距为L，则能击中Q点的电子的最小速率为多大？

解析 P点粒子源发射的粒子朝着四面八方，洛伦兹力的方向也应该朝四面八方。对于发射速率较小的粒子，粒子圆心分布在以P为圆心的“近圆”A上；而对于发射速率越大的粒子，圆心分布在以P为圆心的“远圆”B上。分别在圆弧A和圆弧B上取点作系列圆弧①②③④及⑤⑥⑦⑧。

观察系列圆弧可知，发射粒子的速率越大，圆弧越接近Q点，要让电子击中Q，至少要求“远圆”中的圆弧⑤刚好过点Q，则圆弧⑤半径至少为。

4 讨 论

可见，对于带电粒子在磁场中的物理模型，当粒子的入射速度大小、方向或磁感应强度都唯一确定时，粒子的运动显得较为单一，常规法的使用简捷。然而，在面对多运动轨迹，甚至是不定运动轨迹时，穷举法的优势明显起来，它有效地罗列了可能存在的多种解，化“定圆心”为“定圆心范围”，避“作一圆”为“作系列圆”，增加学生的自信心。其次，该方法并非望文生义地“穷举”，只需要几个典型特征圆（弧）加以观察、筛选即可。在实际运用中，穷举法的思维过程往往显得理所当然而富有直观性[2]。巧借学生的思维延续性强化学生分析、判断、观察实践的综合能力，让学生对粒子的运动特点仿佛感同身受，对学生素质教育中三维目标的有效培养也有较大帮助，有利于学生内化知识，积极动脑，提高思维水平。

参考文献：

[1]王得燕.穷举法与粒子算法的比较[J].无锡技术学院学报，2008，7（1）：44.

[2]郭建斌.例谈穷举法在高中物理教学中的应用[J].技术物理教学，2011，19（4）：58-59.

（栏目编辑 罗琬华）