基于LMD和增强包络谱的滚动轴承故障分析*

2017-03-15杜冬梅

振动、测试与诊断 2017年1期

关键词：特征频率峭度内圈

杜冬梅，张昭，李红，何青

(华北电力大学能源动力与机械工程学院北京，102206)

基于LMD和增强包络谱的滚动轴承故障分析*

杜冬梅，张昭，李红，何青

(华北电力大学能源动力与机械工程学院北京，102206)

针对滚动轴承发生故障时振动信号幅值分布的峭度和歪度都会发生变化的特点，提出基于峭度-歪度的局部均值分解分量筛选准则，将峭度值和歪度绝对值最大的分量筛选出来并重构故障信号，以达到降噪的目的。对降噪后的信号进行增强包络谱分析，得到故障的特征频率。应用提出的新方法对实测的滚动轴承外圈、滚动体和内圈发生故障时的振动信号分别进行了分析。结果表明，基于峭度-歪度的局部均值分解分量筛选准则有效地降低了信号中的噪声，在此基础上应用增强包络谱有效地减少带内噪声影响，从而使故障特征信息凸现出来，有利于对滚动轴承的各种故障进行诊断。

局部均值分解；筛选准则；增强包络谱；滚动轴承；故障诊断

引言

滚动轴承是机械设备中常见的通用部件，其运行状态的稳定关系到整个系统。当其出现局部故障时，轻则使机械设备产生振动和噪声，重则损坏设备造成巨大的经济损失[1-2]。因此，成功地对轴承进行故障预测和诊断具有重要意义。

传统的滚动轴承故障诊断方法是先对故障信号共振频带进行选择，获得中心频率和带宽后选择合适的滤波器对信号进行滤波，然后进行包络分析，得到包络谱来诊断轴承故障[3-4]。但是，故障信号共振频带和滤波器的选择都需要人为干预，对故障诊断的准确性造成了一定影响[5-6]。文献[7]提出基于短时傅里叶变换(short time Fourier transform，简称STFT)的峭度图方法，但其抗干扰性不好，当信号的信噪比较低时，分析结果的准确性受限。文献[8]提出基于聚合经验模态分解(ensemble empirical mode decomposition，简称EEMD)降噪和1.5维谱的方法进行轴承内圈故障的诊断。但是，在对本征模态分量(intrinsic mode function，简称IMF)进行筛选时，采用分量与故障信号的相关系数和峭度筛选准则，当相关系数的阀值设置较高时，容易丢失携带故障信息的分量[9]。

笔者提出基于局部均值分解(local mean decomposition, 简称LMD)降噪和增强包络谱的滚动轴承故障特征提取方法，并在LMD分量选择时，提出峭度-歪度筛选准则。LMD是一种自适应的故障信号分解方法，可以避免因滤波器选择而造成的人为误差。通过对实测的滚动轴承故障信号的分析和诊断，验证了该方法的有效性。

1 LMD原理

LMD可以将原始信号自适应分解为一组频率由高到低自动排列的分量，每个分量由一个纯调频信号和一个包络信号相乘得到。获得纯调频信号和包络信号的过程[10]如下。

1) 寻找原始信号x(t)所有的局部极值点ni，计算相邻两个极值点ni和ni+1的平均值mi

(1)

将所有平均值mi用直线连接起来，用滑动平均方法进行平滑处理，得到局部均值函数m11(t)。

2) 计算局部包络估计值

(2)

将所有包络估计值ai用直线连接起来，用滑动平均方法进行平滑处理，得到包络函数a11(t)。

3) 将局部均值函数m11(t)从原始信号x(t)中分离出来

h11(t)=x(t)-m11(t)

(3)

4) 用h11(t)除以包络估计函数a11(t)以对h11(t)进行解调，得到

(4)

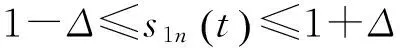
5) 将上述迭代过程中得到的所有包络估计函数相乘，得到包络信号

(5)

6) 将包络信号a1(t)与纯调频信号s1n(t)相乘，得到原始信号的第1个携带有用信息的分量

p1(t)=a1(t)s1n(t)

(6)

7) 将第1个分量p1(t)从原始时间序列x(t)中分离出来，得到一个新的信号u1(t)，再对u1(t)重复以上步骤1～6，循环k次，直到uk为一个单调函数或常数为止。最终可以得到一组携带有用信息的分量和一个残余分量uk，即

(7)

2 峭度-歪度筛选准则

LMD分解可能出现虚假分量，要想重新构造出信噪比较高的故障信号，必须从中筛选出含故障信息较多的分量，再进行故障信号的重构。由于滚动轴承故障初期出现局部点蚀，引起微弱的周期性冲击振动，峭度K为信号幅值分布的4阶统计量，对振动信号中包含的冲击成分非常敏感

(8)

其中：μ为均值；σ为方差；E表示数学期望。

正常轴承的振动信号幅值分布接近正态分布。当出现局部故障时，由于冲击成分增多，幅值分布将偏离正态分布。歪度S为信号幅值分布的3阶统计量，用来衡量信号偏离正态分布的程度。

(9)

随着故障的发生，歪度也会发生变化。

为了消除LMD分解出现虚假分量和信号中的噪声，笔者提出基于峭度-歪度LMD分量筛选准则，即分别求取LMD各分量的峭度和歪度，选取峭度和歪度绝对值最大的分量重构信号。如果峭度最大和歪度绝对值最大的分量为同一个分量，则可以直接用该分量进行分析。实测信号分析验证表明，该分量筛选准则在滚动轴承故障诊断中十分有效。

3 增强包络谱分析

增强包络谱将广义的Shannon熵引入包络解调[11]中，使幅值大于包络幅值标准差的成分得到增强，幅值小于标准差的成分得到削弱。因此，增强包络谱具有减少频带内噪声的作用，改善了滤波信号带内噪声不能被有效滤除的情况。

增强包络谱可通过自相关增强算法实现，具体步骤如下。

1) 计算自相关函数。设原始离散信号为x(n)，其自相关函数为

rx(τ)=E[x(n)x*(n+τ)]

(10)

其中：τ=1,2,…,n-1为时间延迟；x*为x的共轭。

2) 求自相关包络谱。通过Hilbert变换求自相关包络Rx(n+τ)，再进行傅里叶变换求自相关包络谱H(k)。

3) 求增强包络谱。广义Shannon熵定义为

M(x)=H(x)log2H(x)

(11)

由此定义增强包络谱为

(12)

其中：s为包络谱H(k)的标准差。

4 实测信号分析诊断

为了验证方法的有效性，利用美国凯斯西储大学公开的滚动轴承故障数据在Matlab中进行分析。选取电机驱动端SKF6205-RS深沟球轴承故障数据，该轴承的节圆直径为39 mm，内圈直径为25 mm，外圈直径为52 mm，滚动体直径为7.94 mm。轴承缺陷为电火花加工的直径为0.533 4 mm单点点蚀。信号采集时点蚀缺陷位于轴承外圈的最底部，采样频率为12 kHz，分析点数为6 000，电机转轴频率为29.95 Hz。轴承滚动体、外圈和内圈故障的理论特征频率分别为141.17，107.36和162.19 Hz。

4.1 轴承滚动体故障

将轴承滚动体故障信号经均值滤波处理后，做LMD分解得到2个分量和1个残余分量。因残余分量为一个包含许多虚假分量的残余项，故其峭度值和歪度值可直接忽略不计。计算得到轴承滚动体故障信号2个分量的峭度和歪度如表1所示。可以看出，第2分量的峭度和绝对歪度都为最大。因此，根据峭度-歪度筛选准则，可以直接用第2分量作为重构信号。对第2分量计算包络谱和增强包络谱如图1所示。由图1(a)的包络谱只能勉强找到转轴旋转频率(转频)成分为30 Hz，故障特征频率成分均淹没在噪声频谱里。在图1(b)的增强包络谱中不仅可以很容易地找到转频及其2倍频和3倍频成分，还可以容易地找到滚动体故障的特征频率成分138 Hz及其与转频调制的频率成分，由此可以诊断该轴承滚动体出现了故障。

为了说明峭度-歪度筛选准则的有效性，将轴承滚动体故障信号的两个LMD分量相加得到重构的故障信号，并计算其包络谱和增强包络谱，如图2所示。在图2(a)包络谱中可以找到故障特征频率成分，但是其峰值相对较小且受噪声干扰相对严重。在图2(b)增强包络谱中根本找不到故障特征频率成分，因此按照文献[8]提出的相关系数-峭度筛选准则得到的增强包络谱在此不能使用。由此可见，提出的峭度-歪度筛选准则对轴承故障信号的分析和诊断是有效的，同时也说明增强包络谱对于去除带内噪声也是有效的。

表1 滚动体故障时LMD分量的峭度、歪度和相关系数

Tab.1 Kurtosis, skewness and correlation coefficient of LMD product functions of fault at ball

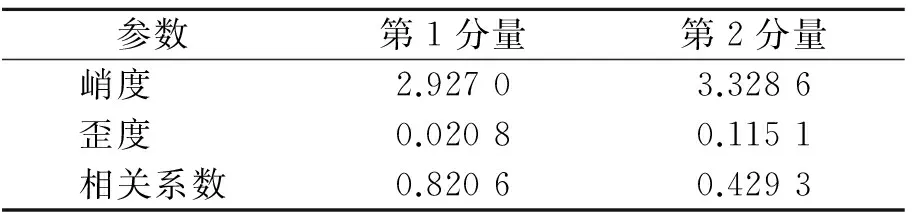
参数第1分量第2分量峭度2.92703.3286歪度0.02080.1151相关系数0.82060.4293

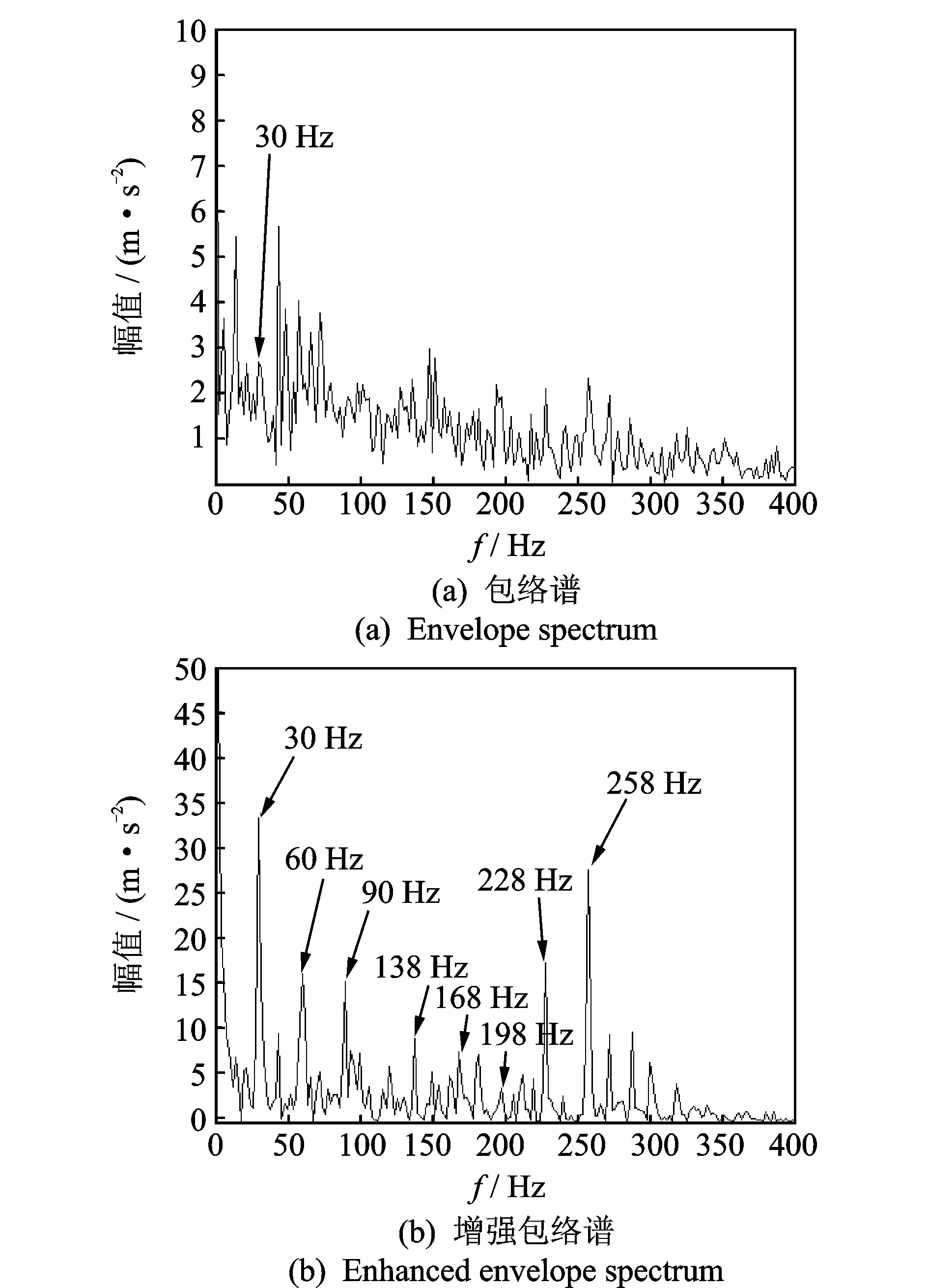
图1 筛选后滚动体故障信号的包络谱分析Fig.1 Envelope spectrum of screened signal of fault at ball

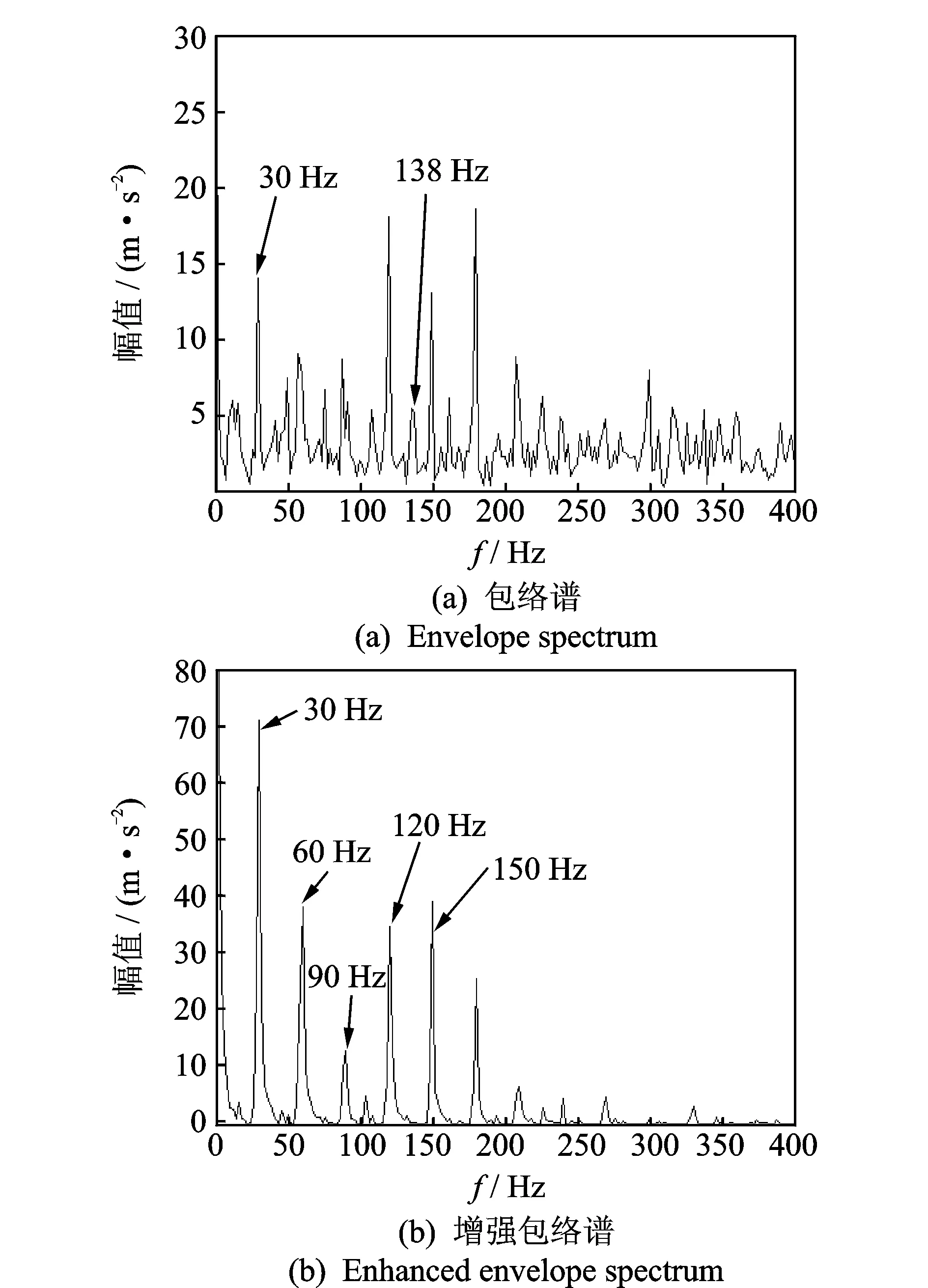
图2 未筛选滚动体故障信号的包络谱分析Fig.2 Envelope spectrum of unscreened signal of fault at ball

4.2 轴承外圈故障

同样，将轴承外圈故障信号经均值滤波后做LMD分解，得到3个分量和1个残余分量。忽略残余项，计算得到3个分量的峭度和歪度如表2所示。由表2可以看出，峭度最大的是第1分量，歪度绝对值最大的是第3分量。根据峭度-歪度筛选准则，选择第1和第3分量进行信号重构，然后对重构信号计算包络谱和增强包络谱，如图3所示。

由图3可以很容易地找到转频成分30 Hz及其2倍频和3倍频、外圈故障的特征频率108 Hz及其与转频调制的边频成分78 Hz和138 Hz。显然，图3(b)的谱线更为清晰，图3(a)中出现众多的带状噪声频率。这表明增强包络谱有效地去除了带内噪声，避免了滤波器滤波后产生的带内噪声干扰，有利于准确发现故障特征频率并进行正确诊断。

表2 外圈故障时LMD分量的峭度和歪度

Tab.2 Kurtosis and skewness of LMD product functions of signal of fault at outer raceway

参数第1分量第2分量第3分量峭度5.33414.22663.8799歪度-0.07310.03230.1216

图3 轴承外圈故障信号的包络谱分析Fig.3 Envelope spectrum of signal of fault at outer raceway

轴承每旋转一周，滚动体经过点蚀产生的振动信号频率都会随转轴周期发生变化。轴承外圈点蚀位置固定，做故障分析较为简单。为方便验证新方法对非平稳信号的有效性，取轴承外圈故障信号的末端2 000点进行分析，根据峭度-歪度准则筛选第1，3分量重构故障信号做时频谱，如图4所示。

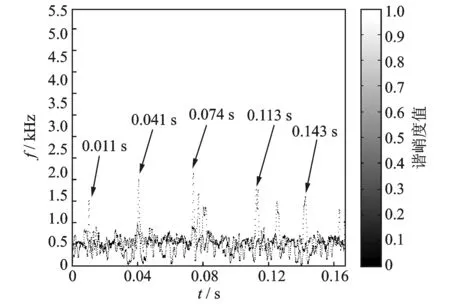
图4 外圈故障时频谱Fig.4 Time-frequency spectrum of outer raceway fault

转轴转速为1 797 r/min，图4中故障信号的LMD分量频率每隔0.3 s就会发生一次变化，与转轴周期恰好相等，证明LMD方法及新的筛选准则对非平稳性信号的分析也有良好效果。

4.3 轴承内圈故障

将轴承内圈故障信号经均值滤波后做LMD分解，得到2个分量和1个残余分量。忽略残余项，计算得到2个分量的峭度和歪度如表3所示。可以看出，第2分量的峭度和绝对歪度都为最大。因此，根据峭度-歪度筛选准则，可以直接用第2分量作为重构信号。对第2分量计算包络谱和增强包络谱如图5所示。

表3 内圈故障时LMD分量的峭度和歪度

Tab.3 Kurtosis and skewness of LMD product functions of fault at inner raceway

参数第1分量第2分量峭度3.849951.7667歪度-0.02802.8329

图5 轴承内圈故障信号的包络谱分析Fig.5 Envelope spectrum of signal of fault at inner raceway

由图5(b)可以容易地找到转频成分30 Hz及其2倍频、突出的内圈故障的特征频率162 Hz及其与转频调制的频率成分，由此可以诊断该轴承的内圈发生了故障。在图5(a)中，转频成分淹没在噪声中，转频的2倍频隐约可见，内圈故障的特征频率也被噪声淹没，因此不能判定该轴承是否出现内圈故障。

5 结论

1) 基于峭度-歪度的LMD分量筛选准则，将滚动轴承故障特征频率的分量筛选出来，有效去除了干扰噪声。

2) LMD分解与增强包络谱结合，进一步减少了频带内的噪声影响，使故障频率成分更加突出，提高了分析的准确性，有利于故障的早期诊断。

3) 自适应LMD降噪与增强包络谱相结合的分析方法能够有效提取滚动体外圈和内圈等常见故障的特征频率成分，可应用于滚动轴承故障的分析与诊断。

[1] 张建军, 王仲生, 芦玉华, 等. 基于非线性动力学的滚动轴承故障工程建模与分析[J]. 振动与冲击, 2010, 29(11): 30-34.

Zhang Jianjun, Wang Zhongsheng, Lu Yuhua, et al. Nonlinear dynamic modeling for localized defects in a rolling element bearing[J]. Journal of Vibration and Shock, 2010, 29(11): 33-34. (in Chinese)

[2] 王天金, 冯志鹏, 郝如江, 等. 基于Teager能量算子的滚动轴承故障诊断研究[J]. 振动与冲击, 2012, 31(2): 1-5.

Wang Tianjin, Feng Zhipeng, Hao Rujiang, et al. Fault diagnosis of rolling element bearings based on Teager energy operator[J]. Journal of Vibration and Shock, 2012, 31(2): 1-5. (in Chinese)

[3] 蔡艳平, 李艾华, 石林锁, 等. 基于EMD与谱峭度的滚动轴承故障检测改进包络谱分析[J]. 振动与冲击, 2011, 30(2): 167-172.

Cai Yanping, Li Aihua, Shi Linsuo, et al. Roller bearing fault detection using improved envelope spectrum analysis based on EMD and spectrum kurtosis[J]. Journal of Vibration and Shock, 2011, 30(2): 167-172. (in Chinese)

[4] 孙伟, 熊邦书, 黄建萍, 等. 小波包降噪与LMD相结合的滚动轴承故障诊断方法[J]. 振动与冲击, 2012, 31(18): 153-156.

Sun Wei, Xiong Bangshu, Huang Jianping, et al. Fault diagnosis of a rolling bearing using wavelet packet de-noising and LMD[J]. Journal of Vibration and Shock, 2012, 31(18): 153-156. (in Chinese)

[5] 陈勇, 孙虎儿, 王志武, 等. 基于提升小波降噪与LMD的转子故障特征提取方法[J]. 矿山机械, 2013, 41(9): 138-142.

Chen Yong, Sun Huer, Wang Zhiwu, et al. A method of extracting rotor fault features based on lifting wavelet de-noising and LMD[J]. Mining & Processing Equipment, 2013, 41(9): 138-142. (in Chinese)

[6] 刘涛涛, 潘宏侠. 应用改进的LMD和小波降噪于滚动轴承故障诊断[J]. 噪声与振动控制, 2014, 34(2): 152-157.

Liu Taotao, Pan Hongxia. Application of improved LMD and wavelet de-noising in rolling bearing's fault diagnosis[J]. Noise and Vibration Control, 2014, 34(2): 152-157. (in Chinese)

[7] Antoni J, Randall R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines[J]. Mechanical Systems and Signal Processing, 2006, 20(2): 308-331.

[8] 唐贵基, 王晓龙. 基于EEMD降噪和1.5维能量谱的滚动轴承故障诊断研究[J]. 振动与冲击, 2014, 33(1): 6-10.

Tang Guiji, Wang Xiaolong. Fault diagnosis for roller bearings based on EEMD de-noising and 1.5-demensional energy spectrum[J]. Journal of Vibration and Shock, 2014, 33(1): 6-10. (in Chinese)

[9] 王增才, 王树梁, 任锴胜, 等. 基于EEMD的提升机天轮轴承故障诊断方法[J]. 煤炭学报, 2012, 37(4): 689-694.

Wang Zengcai, Wang Shuliang, Ren Kaisheng, et al. Research on the method of hoist sheave bearing fault diagnosis based on EEMD[J]. Journal of China Coal Society, 2012, 37(4): 689-694. (in Chinese)

[10]Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.

[11]唐贵基, 王晓龙, 邓飞跃. 改进增强峭度和增强包络谱在滚动轴承故障诊断上的应用[J]. 振动与冲击, 2014, 33(13): 53-58.

Tang Guiji, Wang Xiaolong, Deng Feiyue. Application of improved enhanced kurtogram and enhanced envelope spectrum in fault diagnosis of rolling bearings[J]. Journal of Vibration and Shock, 2014, 33(13): 53-58. (in Chinese)