基于奇异值分解拓展应用的故障特征提取技术*
2017-03-15童水光从飞云董广明
童水光, 唐 宁, 从飞云, 周 懿, 董广明
(1.浙江大学工学部 杭州, 310027)(2.上海交通大学机械系统与振动国家重点实验室 上海, 200240)
基于奇异值分解拓展应用的故障特征提取技术*
童水光1, 唐 宁1, 从飞云1, 周 懿1, 董广明2
(1.浙江大学工学部 杭州, 310027)(2.上海交通大学机械系统与振动国家重点实验室 上海, 200240)
以奇异值分解理论为理论基础,通过对奇异值分解矩阵的架构分析,提出了滑移矩阵序列的架构方法。以该方法为指导,引入差异谱、主奇异和、最大特征值重构和最优化滤波器设计等方法,成功实现了滚动轴承故障特征提取。试验数据分析结果表明,提出的基于滑移矩阵序列奇异值分解的故障特征提取技术对于滚动轴承微弱冲击故障特征具有优越的识别和提取能力,对实现滚动轴承强噪声背景下的故障诊断具有重要意义。
奇异值分解;滑移矩阵;特征提取;滚动轴承;故障诊断
引 言
现代信号处理技术的发展为故障诊断的研究提供了强大的技术支持,故障特征提取技术是故障诊断研究的灵魂,它直接关系到故障诊断的准确性。近年来,各种利用现代信号处理方法实现故障特征提取不断涌现,有快速傅里叶变换、功率谱分析、倒谱分析、自适应滤波技术、时频分析、Winger分布技术、小波分析、谱峭度分析、奇异值分解技术和循环平稳信号分析等,众多方法的引入使得故障诊断技术手段越来越丰富,实现途径也越来越多样化。
奇异值分解(singular value decomposition, 简称SVD)是一种正交变换,它通过将原矩阵转化为一个对角矩阵,从而得到原矩阵的奇异值,可有效反映原矩阵中的一些特性。Huang等[1]将奇异值分解引入到图像处理领域,应用发现该方法对图像恢复具有很好的效果。袁小宏等[2]将奇异值分解方法引入齿轮箱的信号分析中,成功实现了齿轮箱的降噪功能,增加了故障特征提取的准确性。刘献栋等[3]利用奇异值分解技术实现了对信号中突变信息的检测,通过试验论证发现,对于相同噪声背景环境下的信号,奇异值分解方法对突变信息的检测能力好于小波分析方法。
运用奇异值分解方法对机械设备进行故障诊断时,首先需要构造一个相应的分解矩阵。在振动信号分析领域,此分解矩阵一般以相应的时域振动序列为原型来进行构造。分解矩阵的构造方法主要有:观测矩阵、吸引子轨迹矩阵[4]、改进的吸引子轨迹矩阵[5]和症状观测矩阵[6-7]等。实践证明,以上奇异矩阵的架构方法对于机械故障诊断都有较好的效果,但存在不同的适用背景和使用范围。吸引子轨迹矩阵和观测矩阵对瞬时振动信号分析具有较好的效果,但由于它们是对长时间序列进行重构,受到噪声干扰的影响较大,不利于对低信噪比信号的处理。症状观测矩阵主要着眼于设备生命周期内的状态评估和监测,对于某时刻信号的分析和诊断有相对分辨不足的缺点。基于上述研究现状和不足,笔者提出一种基于滑移矩阵序列的奇异值分解算法,它通过对时间序列滑移截取的思路,构建出一个滑移序列,以此序列为基础实现以奇异值分解理论为手段的故障特征提取。
1 SVD拓展应用的故障诊断方法
1.1 滑移矩阵序列的提出
针对目前关于奇异矩阵架构方法存在的不足,从提高冲击局部识别能力的角度出发,考察某离散时间序列x(k),其中:k=1,2,…,N;N为离散时间序列长度。首先建立滑移截取时间矩形窗函数
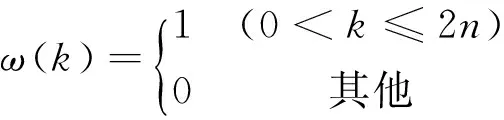
(1)
利用该窗函数对时间序列进行短时截取,获得新的时间序列
yi(k)=x(k)ω(k-(i-1)p)
(2)
其中:yi表示第i次截取后获得了新序列。
笔者在文献[8]给出的滑移向量模型基础上,把二维向量提升为多维矩阵形式,具体表示为
(3)
定义Vi为“滑移矩阵”,其组成的序列即为滑移矩阵序列,所谓的“滑移”定义则表现在参数p的确定上。根据滑移矩阵的定义过程,对其相关参数作如下约定
Nw=2n
(4)
其中:Nw为分析长度。
根据滑移矩阵的截取过程定义,定义的滑移参数p的限定范围为
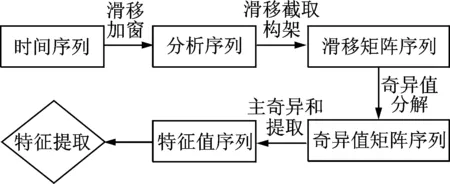
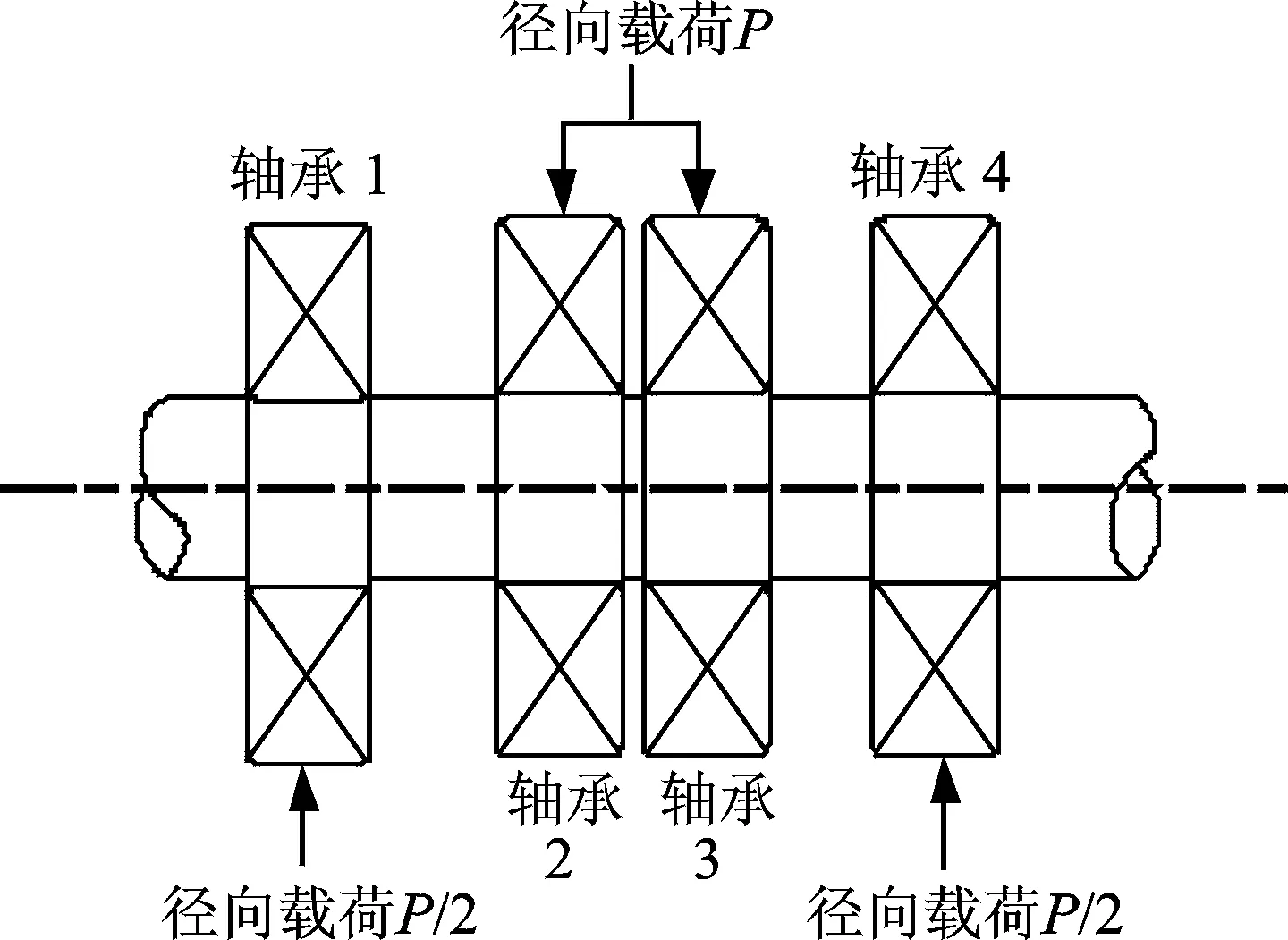
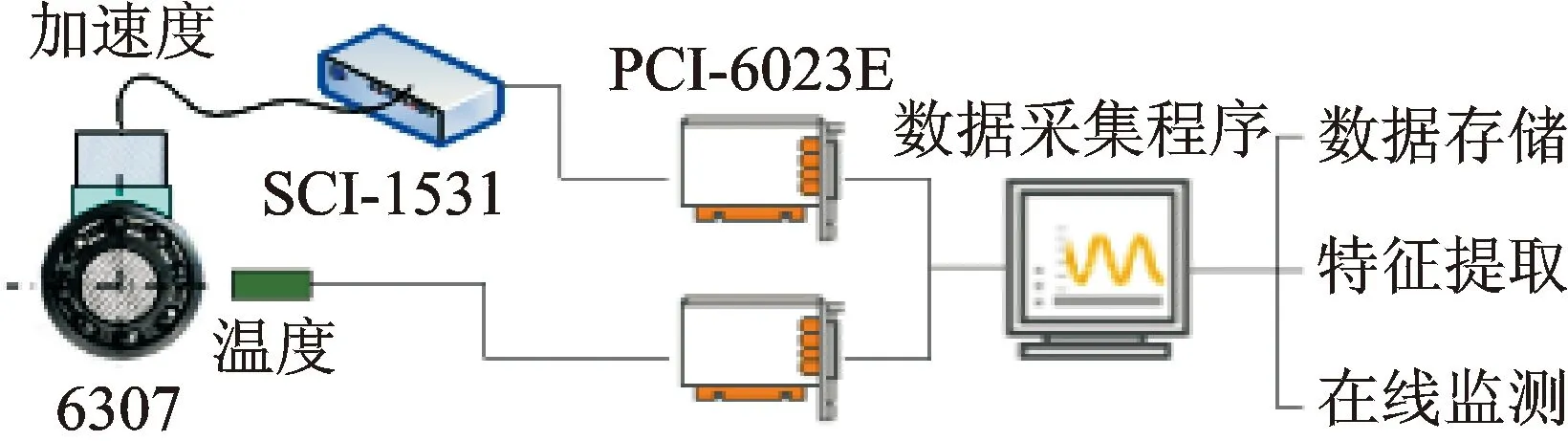
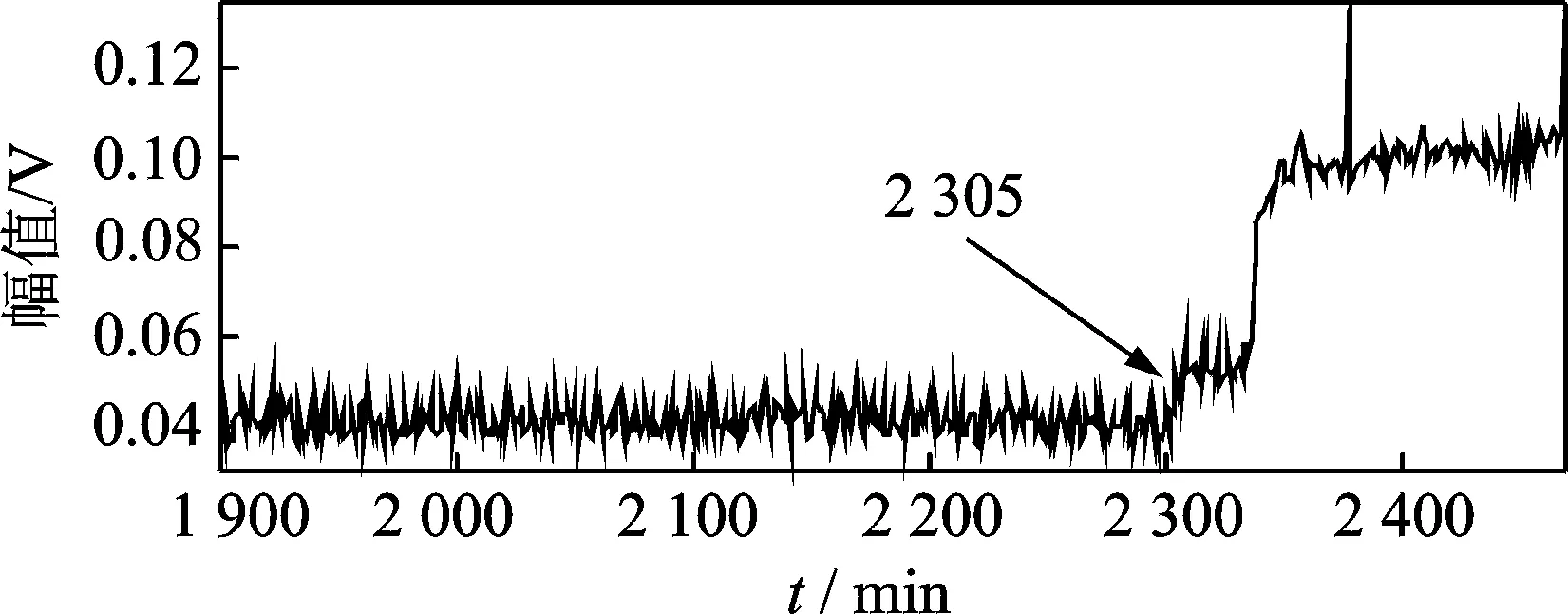
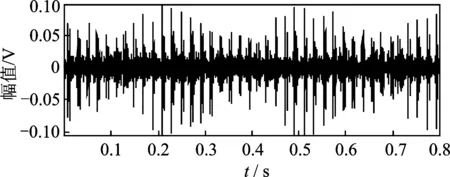
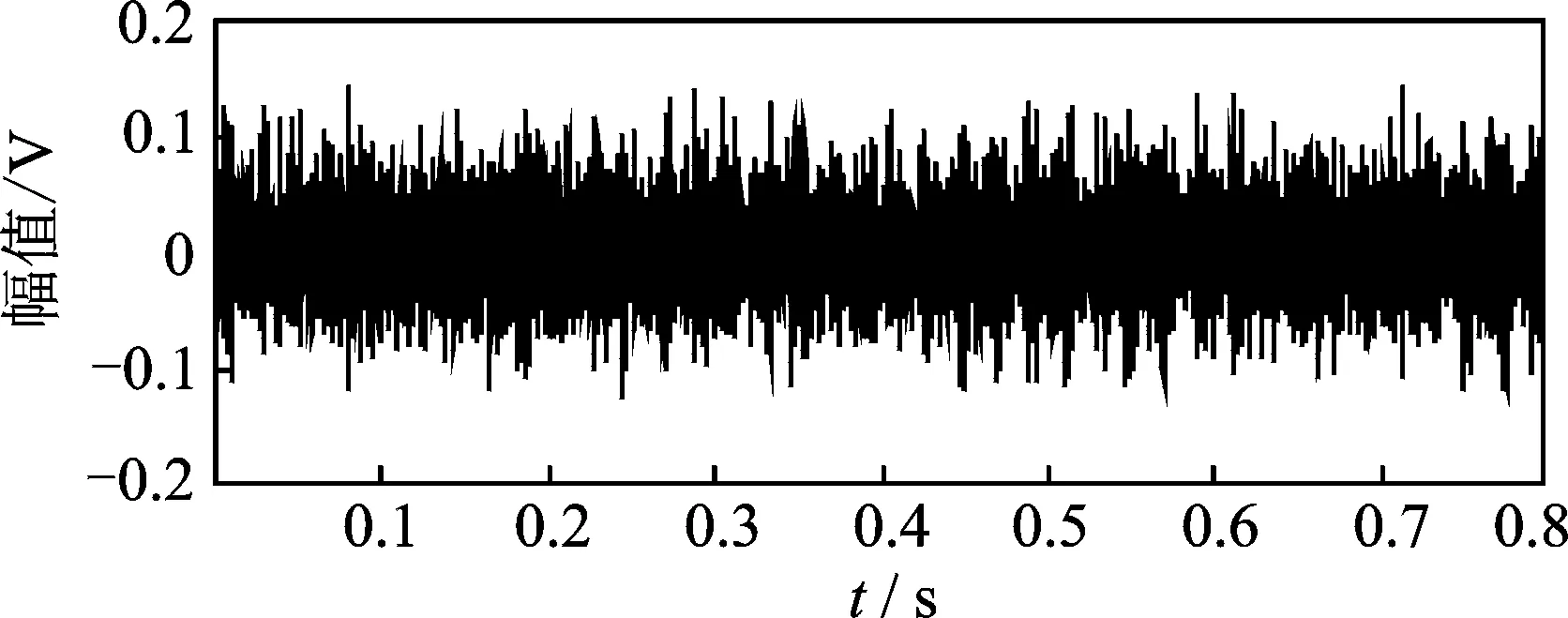
1 (5) 滑移矩阵序列可表示为 S={V1,V2,…,Vm} (6) 其中:m为滑移矩阵序列的长度。 分析长度Nw、原时域序列总长度N和滑移矩阵序列长度m之间的关系满足 (7) 由式(7)可知,滑移参数p对滑移矩阵序列的长度m影响较大,而p的选取必须满足式(5),若p的取值大于Nw,则会出现截取“泄漏”的现象,进而造成分析结果的失真。分析长度Nw对结果的影响也较大, 引入差异谱表示方法 (8) 图1为某噪声水平为-4dB的信号在不同分析长度下差异谱的表现。由图可知,分析长度的选择存在最优合理选择区间,而该阶数确定与原信号的噪声湮没水平相关。 图1 -4dB信号差异谱表现Fig.1 Difference spectrum of signal with -4dB noise level 1.2 基于滑移矩阵架构的特征提取技术 在提出滑移矩阵的架构思想后,如何利用该架构与奇异值分解方法有机结合,实现故障特征提取是笔者介绍的重点内容。将奇异值分解算法融入滑移矩阵,可得出如下分解过程 (9) (10) 其中:σi为第i滑移矩阵的奇异值。 由式(6)和式(9)得到奇异值矩阵序列D (11) 式(11)中每个奇异值对角矩阵所包含的奇异值信息可有效反映对应的滑移矩阵所包含的信息。根据齿轮故障信号原理,可以把振动信号分为冲击主要区域和噪声主要区域。在冲击主要区域,奇异值对角矩阵有一个陡坡的突变,尤其是前两阶奇异值偏大;而在噪声主要区域内,对角矩阵奇异值变化比较平缓,前两阶奇异值相对偏小。根据以上分析,利用得出的奇异值对角矩阵信息,引入“主奇异值和”指标函数对该序列进行分析和处理,得到新的特征指标 Ri=σi1+σi2(i=1,2,…,m) (12) 其中:Ri为第i滑移矩阵的前两个主奇异值之和,称其为“主奇异和”;σi1和σi2分别为第i滑移矩阵的第1和第2奇异值。 依次对滑移矩阵序列进行特征指标提取,得到对应的主奇异和序列为 SR={R1,R2,…,Rm} (13) 将该序列编号与时间坐标建立逻辑对应关系,得到和原始时域信号对应的特征序列。 图2 特征提取算法流程Fig.2 The diagram of feature extraction 1.3 故障冲击智能识别技术 在机械设备故障诊断研究领域,故障振动信号经常表现为冲击的形式[9],该冲击发生后将被调制到高频带区,在时间波形上则表现为冲击振荡衰减的形式。笔者在利用滑移矩阵序列特征提取技术的基础上,分析故障冲击形成机理及其演化过程,建立机械设备故障冲击智能识别及诊断体系。SR代表了对应时域信号段内的故障特征大小,获取最大特征量为 RK=max(Ri) (i=1,2,…,m) (14) 其中:K为最大特征量在序列中的序号。 根据滑移矩阵序列的架构思想及故障冲击时域表现特征,可知最大特征量对应的滑移矩阵包含丰富的故障信息。因此,利用下式对包含丰富故障信息的时间序列进行重构 y=(x((K-1)p+1),…,x((K-1)p+2n)) (15) 短时序列对于故障冲击衰减信息的获取具有重要的指导作用。图3为某滚动轴承故障信号经特征提取后其最大特征值重构后获得的短时时间序列,表现出了较为明显的周期振荡波形。图4为对应的频域结构图,结合冲击故障高频振荡衰减模型原理,该频域分析图为冲击共振频率及频带宽度的获取提供了有力的技术支撑。 图3 短时重构时域序列Fig.3 Short-time reconstruction time series 图4 短时重构序列频域响应Fig.4 Frequency response of short-time reconstruction series 利用短时冲击序列的故障信息参数,设计合理的最优化滤波器,可有效实现故障冲击的智能识别[10]。最优化滤波器设计过程重要的信息参数有:中心频率、滤波器带宽及滤波器阶数。笔者拟在综合利用故障信息参数的基础上,设计故障冲击识别最优化滤波器,该设计思想将以信号共振频带的动态获取及跟踪为核心技术环节,以滤波带宽设计为重要过程,实现故障冲击信号的智能识别和提取。 实现最优化滤波器设计,首先利用下式获得短时重构的序列频域表达式 (16) 其中:y(z)为短时重构序列;Nw为短时重构序列的长度(分析长度);Y(k)为对应频域表达式。 引入以(fc, Δf)为表达形式的滤波器设计方法,其中:fc为待设计滤波器G(f)的中心通过频率;Δf为G(f)的滤波带宽。对应设计参数计算公式为 (17) 其中:fs为采样频率。 所得到的以(fc, Δf)为基础的最优化滤波器G(f)综合考虑了共振频率的识别精度和带宽设置的性能平衡问题,能够有效克服中心频率识别精度和带宽Δf设置之间“错位”的风险,实现在保证滤波器中心通过频率识别准确性的前提下最大化地提高冲击特征提取能力。 为论证提出的特征提取技术在故障诊断领域的作用,特将该技术应用于滚动轴承的故障特征提取及诊断。利用滚动轴承试验台对型号是6307的滚动轴承进行全寿命试验,故障类型为内圈点蚀故障,试验装置示意图及传感器安装如图5和图6所示。依据全寿命过程振动数据,可获取滚动轴承早期故障信号用于论证笔者提出的故障特征提取技术的优越性。振动信号通过加速度传感器首先经过NI信号调理模块进行抗混叠滤波处理,然后接入NI的PCI数据采集卡6023E进行数据采集,相关的采集软件使用Labview平台进行编写,设置系统采样频率为25.6kHz,每一组振动信号数据的保存时间间隔为1min,每组数据20 480个数据点。设备从开始到出现报警,共采集2 469组数据,根据全寿命2 469组数据的RMS值,前1 900组数据表现出正常的振动信号,为更加明确表现故障振动加大时的特征表现,图8截取了1 900组以后的数据进行展现。 图5 轴承加载示意图Fig.5 Schematic diagram of bearing load 图6 试验装置示意图Fig.6 Schematic diagram of experimental setup 图7 全寿命RMS局部放大示意图Fig.7 Local enlargement of whole life RMS 图8 第2 305组数据时域波形Fig.8 Time series of No.2 305 针对图8所示的时域波形信号,利用笔者提出的方法进行故障冲击特征提取和最优滤波后,得出的时域波形信号如图9所示。由图9可知,笔者提出的故障特征提取方法对于滚动轴承在运行过程中产生的冲击故障特征具有良好的提取作用,该时域波形表现出了明显的冲击特性,与滚动轴承故障特征表现模型吻合,可得出滚动轴承处于故障状态。为显示提出方法的有效性和优越性,引入AR预测滤波器技术对图8所示的信号进行分析处理[9]。图10为原信号经过AR预测滤波器滤波后得到的时域信号。与图9相比,其故障冲击特征表现不明显,整体噪声也未得到有效抑制。 通过上述对比分析可知,笔者提出的基于滑移矩阵序列SVD分解算法的滚动轴承故障诊断模型对于滚动轴承的微弱故障特诊的识别具有不错的效果,尤其是针对滚动轴承的故障冲击,可以有效提取出强噪声背景下的微弱冲击特征,对滚动轴承的故障诊断及状态监测具有重要意义。 图9 最优滤波后的时域信号Fig.9 The time series filtered by optimal filter 图10 AR预测滤波器滤波后的时域波形Fig.10 The time series filtered by AR prediction filter 通过对奇异值分解方法的理论研究分析,结合滑移矩阵序列架构方法,成功实现了对滚动轴承微弱故障的特征提取。以奇异值分解理论为依据,围绕分解矩阵架构展开详细分析建模,成功实现了滚动轴承的故障特征提取。通过试验数据分析可知,笔者提出的基于滑移矩阵序列奇异值分解的故障特征提取技术对于滚动轴承的微弱故障信号特征具有很好的识别提取作用。通过对比研究发现,该方法在滚动轴承运行过程中的振动信号微弱冲击特征增强方面具有很好的效果。 [1] Huang T S, Narendra P M. Image restoration by singular value decomposition[J]. Applied Optics, 1975, 14(9): 2213-2216. [2] 袁小宏, 史东锋. 奇异值分解技术在齿轮箱故障诊断中的应用研究[J]. 化工机械,1997,24(6): 324-327. Yuan Xiaohong, Shi Dongfeng. Solid-borne sound monitoring in grinding of hard brittle Nonmetal work [J]. Chemical Engineering & Machinery, 1997, 24(6): 324-327.(in Chinese) [3] 刘献栋, 杨绍普. 基于奇异值分解的突变信息检测新方法及其应用[J]. 机械工程学报,2002, 38(6): 102-105. Liu Xiandong, Yang Shaopu. New method of detecting abrupt information based on singuarity value decomposition and its application[J]. Chinese Journal of Mechanical Engineering, 2002, 38(6): 102-105.(in Chinese) [4] Takens F. Dynamical systems and turbulence, warwick 1980[M]. New York:Springer Berlin Heidelberg, 1981: 366-381. [5] 陈恩利, 吴勇军, 申永军, 等. 基于改进奇异值分解技术的齿轮调制故障特征提取[J]. 振动工程学报,2008,21(5): 530-534. Chen Enli, Wu Yongjun, Shen Yongjun,et al. An improved method of detecting modulated gear fault characteristic based on singularity value decomposition[J]. Journal of Vibration Engineering,2008,21(5):530-534.(in Chinese) [6] Cempel C. Multidimensional condition monitoring of mechanical systems in operation[J]. Mechanical Systems and Signal Processing, 2003, 17(6): 1291-1303. [7] Cempel C. Decomposition of symptom observation matrix and its optimization in vibration condition monitoring of machines[J]. Applied Mechanics and Materials, 2008, 9: 51-60. [8] Cong F, Chen J, Dong G, et al. Short-time matrix series based singular value decomposition for rolling bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2013, 34(1): 218-230. [9] Cong F, Chen J, Dong G. Research on the order selection of the autoregressive modelling for rolling bearing diagnosis[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2010, 224(10): 2289-2297. [10]Randall R B, Antoni J. Rolling element bearing diagnostics-a tutorial [J]. Mechanical Systems and Signal Processing, 2011, 25(2): 485-520. 10.16450/j.cnki.issn.1004-6801.2017.01.010 *国家自然科学基金资助项目(51305392);中国博士后科学基金资助项目(2013M540489);飞行器海上测控实验室开放基金资助项目(FOM2014OF11);浙江省重大科技专项基金资助项目(2012C01021-2) 2015-02-09; 2015-06-04 TH165.3; TN911; TH17 童水光,男,1960年9月生,教授。主要研究方向为重大技术装备的轻量化设计及故障诊断技术。曾发表《Investigation of the dynamic characteristics of a dual rotor system and its start-up simulation based on finite element method》(《Journal of Zhejiang University:Science A》 2010, Vol.14,No.4)等论文。 E-mail:cetongsg@163.com


2 试验论证

3 结束语

