基于LTSA和RVM的复合材料损伤预测分析*

2017-03-15崔建国张文生齐义文于明月朴春雨周志强

振动、测试与诊断 2017年1期

关键词：复合材料向量样本

崔建国，张文生，齐义文，于明月，朴春雨，周志强

(1.沈阳航空航天大学自动化学院沈阳，110136) (2.沈阳飞机设计研究所沈阳，110035)

基于LTSA和RVM的复合材料损伤预测分析*

崔建国1，张文生1，齐义文1，于明月1，朴春雨2，周志强2

(1.沈阳航空航天大学自动化学院沈阳，110136) (2.沈阳飞机设计研究所沈阳，110035)

提出一种基于局部切空间排序(local tangent space alignment，简称LTSA)和相关向量机(relevance uector machine，简称RVM)相结合的复合材料结构损伤演化与预测模型。针对复合材料结构损伤特性，采用疲劳振动试验进行结构损伤预测研究。首先，采用总体平均经验模态分解(ensemble empirical mode decomposition，简称EEMD)方法对多传感器采集的复合材料结构健康信息进行自适应分解，得到不同传感器下的多个本征模态分量(intrinsic mode function，简称IMF)，并对IMF进行希尔伯特(Hilbert)变换，得到相应的Hilbert边际谱能量作为各传感器的特征信息；然后，采用LTSA进行多特征降维融合得到特征能量，对降维融合后得到特征能量采用距离形态相似度方法定义结构健康指数；最后，将结构健康指数作为建模数据，创建RVM预测模型，并通过预测结构健康指数完成复合材料结构损伤预测研究。验证结果表明，该模型可有效地对复合材料结构损伤进行预测。

复合材料; 结构损伤预测; 局部切空间排序; 相关向量机

引言

复合材料由于具有比强度高、比模量高、抗疲劳能力强和抗振能力强等优点，广泛应用于航空航天和国防工业等领域。例如：空中客车A380的设计制造中，复合材料的用量约为结构总质量的25%；F35战斗机其复合材料的使用量约占结构总质量的35%[1]。复合材料在使用过程中容易出现不同形式的结构损伤，从而导致结构失效、性能降低，甚至产生灾难性的后果。因此，对复合材料结构损伤进行预测具有重要意义。

复合材料结构损伤机理复杂，影响因素繁多，其失效形式与金属材料结构具有显著不同，很难找出明确的函数关系来表征结构损伤状态，这使得进行复合材料结构损伤预测显得尤为困难[2]。为了能够很好地预测复合材料结构损伤状态，很多学者致力于该领域的研究，并取得了一定成果。孙中雷等[3]采用有限元分析方法，创建了胶接修补复合材料层合板损伤演变与剩余强度的渐进损伤预测模型，为复合材料损伤预测提供理论基础。马存旺等[4]以粘聚区模型为基础，建立了在常幅载荷复合材料的损伤-寿命与应变能释放率-寿命之间的关系，阐述了在变幅载荷情况下界面损伤累积的相应计算方法与分层疲劳寿命预测流程。张熠卓等[5]通过局部切空间排序算法对高维非线性数据集进行数据降维，得到处理后的低维数据，进而对转子故障特征数据集进行研究。孙志刚等[6]提出了一种基于经验模态分解(empirical mode decomposition，简称EMD)与相关向量机相结合的电力短期负荷预测方法，进而推动了RVM算法在预测领域研究。

基于多位学者在复合材料结构损伤预测领域的研究、LTSA算法具有降维优势及RVM算法在电力短期负荷预测的应用，笔者将LTSA及RVM算法应用在复合材料结构损伤预测领域。复合材料结构损伤预测实现过程如下：首先，对多传感器采集的状态信息进行总体平均经验模态分解，分别提取其Hilbert边际谱能量特征；然后，利用LTSA进行特征层降维融合，对降维融合后得到的状态特征采用距离形态相似度方法确定结构健康指数；最后，将结构健康指数重构后得到的数据作为建模数据构建RVM预测模型，利用RVM预测模型完成复合材料结构损伤预测效能，从而实现了复合材料结构损伤预测效能。

1 理论基础

1.1 局部切空间排列算法

LTSA是一种基于局部线性假设的非线性流形学习算法。其主要思想是：首先，通过K-近邻法寻找每个样本点的邻域，利用各个样本点邻域的切空间构建局部几何特性；然后，计算各个样本点在局部切空间的投影得到局部低维坐标；最后，经局部仿射变换最终得到整体低维嵌入坐标[7]。算法实现的具体步骤如下。

1) 邻域空间构造

对于本研究的复合材料损伤预测，设高维数据集为S=[s1,s2,…，sn]，其中：si∈Rm(i=1,2,…,n)是一个样本集，即复合材料某健康监测传感器的边际谱能量集；n为传感器个数。采用K-近邻方法构建邻域空间，计算每个样本点si与其他样本点的欧式距离，选择包括样本点自身在内的k个距离最小的样本点即可以组成当前样本点的邻域空间，表示为Si=[si1,si2,…sik]，其中，k为紧邻点的个数。

2) 局部低维坐标拟合

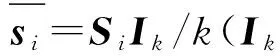
3) 局部坐标放射变换

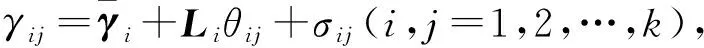
(1)

采用重构误差最小化方法，实现仿射变换中尽可能多的保留局部低维几何信息，即

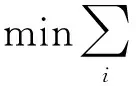
(2)

最终得到最优的低维全局坐标Y。

1.2 结构损伤指数

在复合材料结构损伤预测中，为了将复合材料结构损伤的微小变化进行量化处理，采用距离形态形似度方法定义结构损伤指数，距离形态相似度将马氏距离和向量形态参数相结合，是一种距离相似度与形态相似度相结合的估计方法[8]。为了有效地反映不同向量之间的距离相似程度，将马氏距离引入距离形态相似度估计中。

完好状态向量X=(x1,x2,…,xk)和裂纹出现状态Y=(y1,y2,…,yk)为两个k维向量。定义由状态向量组X和Y之间的马氏距离为

DISXY=[(X-Y)′Σ-1(X-Y)]1/2

(3)

其中：Σ为两个向量组的协方差矩阵。

采用向量形态参数反映两个未知向量之间的形态相似程度，定义为

(4)

其中：VDB为向量差值之和的绝对值；DBV为向量差值之间的绝对值之和。

由式(3)和式(4)得到两个状态向量组X和Y的距离形态相似度评估值DSSVXY为

(5)

按照式(5)定义方式，得到完好状态向量组Sg与裂纹出现状态向量组Sf的距离形态相似度评估值DSSVgf，当前状态向量组Sc与完好状态向量组Sg的距离形态相似度评估值DSSVcg以及当前状态向量组Sc与裂纹出现状态向量组Sf的距离形态相似度评估值DSSVcf。最终得到复合材料结构损伤指数为

(6)

由定义的复合材料结构损伤指数公式可知，当复合材料处于完好状态时SHI=1，当复合材料处于裂纹出现状态时SHI=0。SHI越接近于1，表示复合材料结构损伤程度越低，越接近完好状态；SHI越接近于0，表示复合材料结构损伤程度越高，越接近裂纹出现状态。

1.3 相空间重构

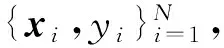
1.4 相关向量机

RVM是一种基于稀疏贝叶斯框架下的机器学习方法[6,9]。与支持向量机(support vector machine，简称SVM)相比，RVM解决了核函数选取必需满足Mercer条件的缺点及相关向量个数少于支持向量个数等优点。因此，尝试将RVM模型引入复合材料进行结构损伤预测研究。

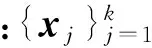
(7)

其中：w为权值向量；K(x,xj)为核函数；b为附加噪声，且满足期望为0、方差为σ2的Gaussian分布。

RVM模型的求解就是寻找输入样本中的核心特征，即相关向量的过程。通过在权值向量w上定义由超参数控制的Gaussian先验概率，在稀疏贝叶斯框架下进行模型训练；采用自相关判定理论来剔除不相关向量，从而获得稀疏化模型。具体的模型推导过程如下。

假设训练样本集S相互独立，t服从期望为y的正态分布，且{t-y}服从期望为0，方差为σ2的正态分布N(0,σ2)。{t-y}的似然函数可表示为

其中：w=(w0,w2,…,wk)T为权值向量；Φ=[φ(x1),φ(x2),…，φ(xk)]T为核函数组成的结构矩阵；φ(xj)=[1,K(xj,x1),…，K(xj,xk)]T。

由于对参数w和σ2的极大似然估计容易出现过适应现象，因此定义w的自相关判定理论先验概率分布为

(9)

其中:α=[α0,α1,…,αk]T为k+1维超参数向量。

给定似然函数以及和先验分布后，根据贝叶斯公式可得后验分布为

(10)

预测概率模型改为

由于式(11)无法直接求解，故将后验分布p(w,α,σ2|t)进行分解

p(w,α,σ2|t)=p(w|t,α,σ2)p(α,σ2|t)

(12)

其中：正态分布的后验期望值μ=σ-2ΣΦTt，协方差Σ=(σ-2ΦTΦ+A)-1，A=diag(α0,…,αk)，代入式(11)得

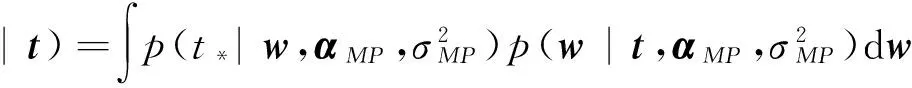
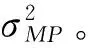
2 复合材料结构损伤预测方法

笔者提出了一种基于LTSA和RVM相结合的复合材料结构损伤演化与预测方法，对复合材料结构损伤预测进行了研究，具体实现过程如下。

1) 数据获取及其预处理。结合复合材料结构损伤机理及结构损伤不同表征方式，采用相应的结构损伤试验(笔者采用疲劳振动试验)进行复合材料结构损伤研究。为获取准确信息，采用多个振动加速度传感器在试验件上进行布局(布局情况如图3所示)，构建传感器网络多方位募集结构件状态信息，并对采集的复合材料原始状态信息进行相应的预处理，提高原始数据的有效性，为损伤预测提供有效数据。

2) 原始状态信息的特征提取。由于传感器获取的信息量大，为了提升损伤预测的时效性，需要对获取的大量数据进行特征提取并提取其状态有效特征。在疲劳振动试验过程中随着损伤的扩展其能量特征不断减弱，笔者采用EEMD方法对各个传感器采集的原始状态信息进行自适应分解，得到各阶本征模态分量，然后对IMF进行Hilbert变换，最终提取Hilbert边际谱能量作为各个传感器的特征信息。

3) 多特征信息融合与定义结构损伤指数。考虑到单一传感器信息特征对表征复合材料结构健康特性具有较大的局限性，笔者采用LTSA方法对多传感器信息提取特征，在特征层上进行降维融合。充分利用每个传感器的Hilbert边际谱能量特征，将降维融合后的特征能量定义为结构损伤指数，作为复合材料结构健康状态特征信息，用此信息对复合材料结构损伤进行预测研究。

4) 复合材料损伤预测模型创建与预测试验。首先，对结构损伤指数获得的数据进行重构，重构后得到训练样本和目标样本；然后，根据建模个数创建复合材料结构损伤预测模型；最后，采用创建的预测模型，输入当前状态训练样本集对复合材料损伤进行预测研究，实现复合材料损伤预测。复合材料结构损伤预测方案如图1所示。

图1 复合材料结构损伤预测方案Fig.1 Prediction method of composite structural damage

3 预测试验研究

3.1 健康数据获取

采用试验件为224 mm×125 mm×2 mm的复合材料层合板(T300/QY8911)，试验前首先对试验件扫频，得到其固有频率为70 Hz；然后，将试验件固定在振动试验台上，持续加载频率为70 Hz的振动信号；最后，用光纤加速度传感器采集试验件的振动加速度。

为准确描述传感器布局，按试验件实际尺寸绘制试验件示意图如图2所示。在试验件上布置两个低频加速度传感器，传感器中心位置为图2中所示小孔的圆心。其中：A，B通道传感器布置在图示下、上方且位于宽边中心。试验件上端为夹持端，夹持长度为20 mm。试验件传感器布局实物图如图3所示。

图2 试验件示意图(单位：mm)Fig.2 Schematic diagram of testing part(unit:mm)

图3 振动试验示意图Fig.3 Schematic diagram of vibration test

完成传感器布局设计后，采用传感器网络分别对复合材料在完好状态和裂纹出现状态进行健康状态信息采集，采样频率为1 kHz。每种状态连续采集4 min得到两组样本集，每组样本集有24万个采样值，通过无损检测测得裂纹出现状态下的裂纹长度为2.7 mm，裂纹出现位置如图3红圈所示。为缩短试验时间，采用带轻微损伤的试验件进行加速试验，用相同的采样频率对当前状态连续采集，得到当前状态下的结构健康状态信息样本集。

3.2 特征层融合

由于传感器获取的信息量大，为提升损伤预测的时效性，笔者采用EEMD方法对各传感器采集的原始信息进行自适应分解并提取Hilbert边际谱能量作为各个传感器的特征信息。

以在完好状态下传感器A采集的24万个采样点为例进行EEMD自适应分解，并提取Hilbert边际谱能量进行分析。首先，对24万个原始数据进行分组，每组包含6 000个采样点，共分成40组；然后，对每组采样信息进行EEMD自适应分解，得到各阶IMF和残余分量[10]。图4为传感器A采集得到的第1组状态信息，即前6 000个采样点进行EEMD分解。最后，对各阶IMF进行Hilbert变换并提取Hilbert边际谱能量特征[11]。

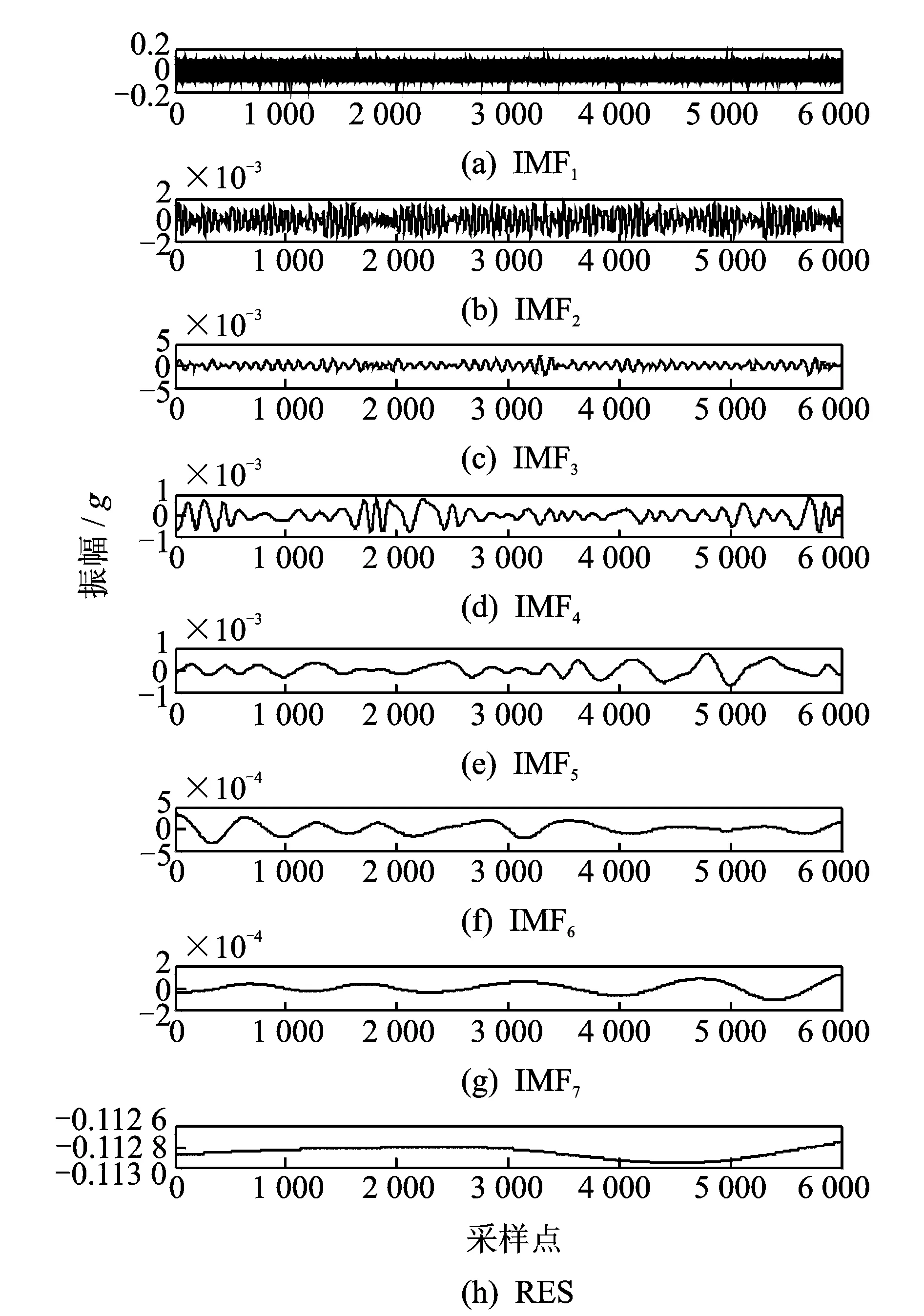
图4 传感器1采集第1组结构状态信息EEMD分解Fig.4 The first group of structural state information acquired via sensor 1 decomposed by EEMD

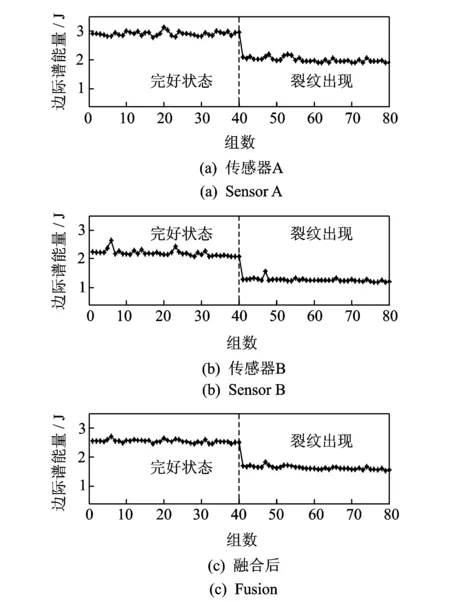
图5 多传感器多边际谱能量特征信息融合Fig.5 Characteristic information fusion of multi-sensors marginal energy

采用与完好状态下传感器A提取Hilbert边际谱能量特征相同的方法分别对传感器A，B采集的裂纹出现状态及传感器B采集的完好状态信息进行EEMD自适应分解，并提取Hilbert边际谱能量。

从图3可知，裂纹出现位置与传感器B较为接近，所以复合材料在完好状态和裂纹出现状态传感器B采集的状态信息经过特征提取得到的Hilbert边际谱能量特征较为准确。如果选取传感器B的Hilbert边际谱能量特征表征复合材料总体结构健康状态，必然有一定的局限性。因此，笔者采用LTSA方法对两个传感器的Hilbert边际谱能量特征进行融合，具体实现过程如下。

采用LTSA算法对传感器A，B的边际谱能量信息进行融合，得到融合后的边际谱能量值为E=[2.565 5,…,1.550 0]80×1。各个传感器提取的Hilbert边际能量特征与降维融合后的结果如图5所示。由图5可知，当复合材料在不同健康状态下完全可以由降维融合后的特征能量唯一表征，为复合材料结构损伤预测提供完备的数据特征。同理，对当前状态不同传感器采集的采样值进行分组，每组6万个采样点即1 min采集的值为一组，进行EEMD自适应分解并提取Hilbert边际谱能量，通过LTSA算法对不同传感器获取的边际谱能量进行降维融合，创建当前状态下融合后的状态特征矩阵Ed，利用结构损伤指数理论得到当前状态下复合材料结构损伤指数SHI=[ 0.929 1,0.900 8, …]。

3.3 结构损伤预测

将SHI进行相空间重构后得到的数据作为建模数据，创建RVM预测模型，采用动态预测机制完成复合材料结构损伤预测研究。具体步骤如下：首先，根据文献[12]的结论，如果待预测的时间序列数据量不是很大，相空间重构个数一般可以选择3～5。因此将SHI作为输入进行相空间重构，重构个数选择5，得到创建RVM模型所需的训练样本及目标样本，如表1所示。

表1 重构后当前状态的结构损伤指数

Tab.1 The current state of the structural damage index after reconstructing

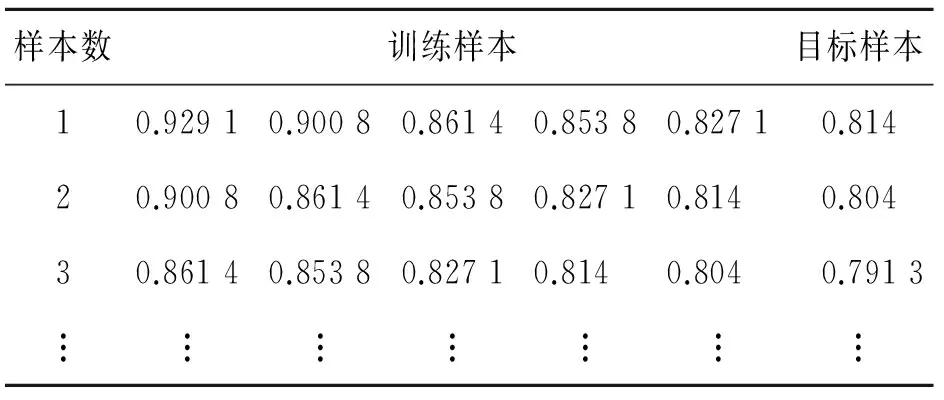
样本数训练样本目标样本10.92910.90080.86140.85380.82710.81420.90080.86140.85380.82710.8140.80430.86140.85380.82710.8140.8040.7913︙︙︙︙︙︙︙

然后，采用动态预测机制进行动态建模，固定每次建模样本个数为L=25，每次向后预测5个结构损伤指数值，即5 min内的结构损伤指数值，累计预测多次直到完成最后的结构损伤预测工作。因此，第1次建模是从训练样本和目标样本选出1～25个样本创建RVM模型，预测时训练样本选出26～30个样本，并向后预测5个结构损伤指数值，即第31～35个结构损伤指数值。如果预测得到的结构损伤指数非常接近于0，则表明轻微冲击损伤试验件进行加速试验30 min后出现的裂纹长度为2.7 mm，否则进行第2次建模。第2次建模是从训练样本和目标样本选出6～30个样本创建RVM模型，同样向后预测5个结构损伤指数值并与0进行比较，判断当前状态结构损伤程度。依此类推，经过多次建模可以预测出未来一段时间内的复合材料健康状态。

由于RVM算法解决了SVM核函数的选取必需满足Mercer条件的缺点，极大地减少了核函数的计算量。为了测试RVM预测模型的准确性，采用相同的预测机理与建模数据创建SVM预测模型，具体预测结果如图6所示。

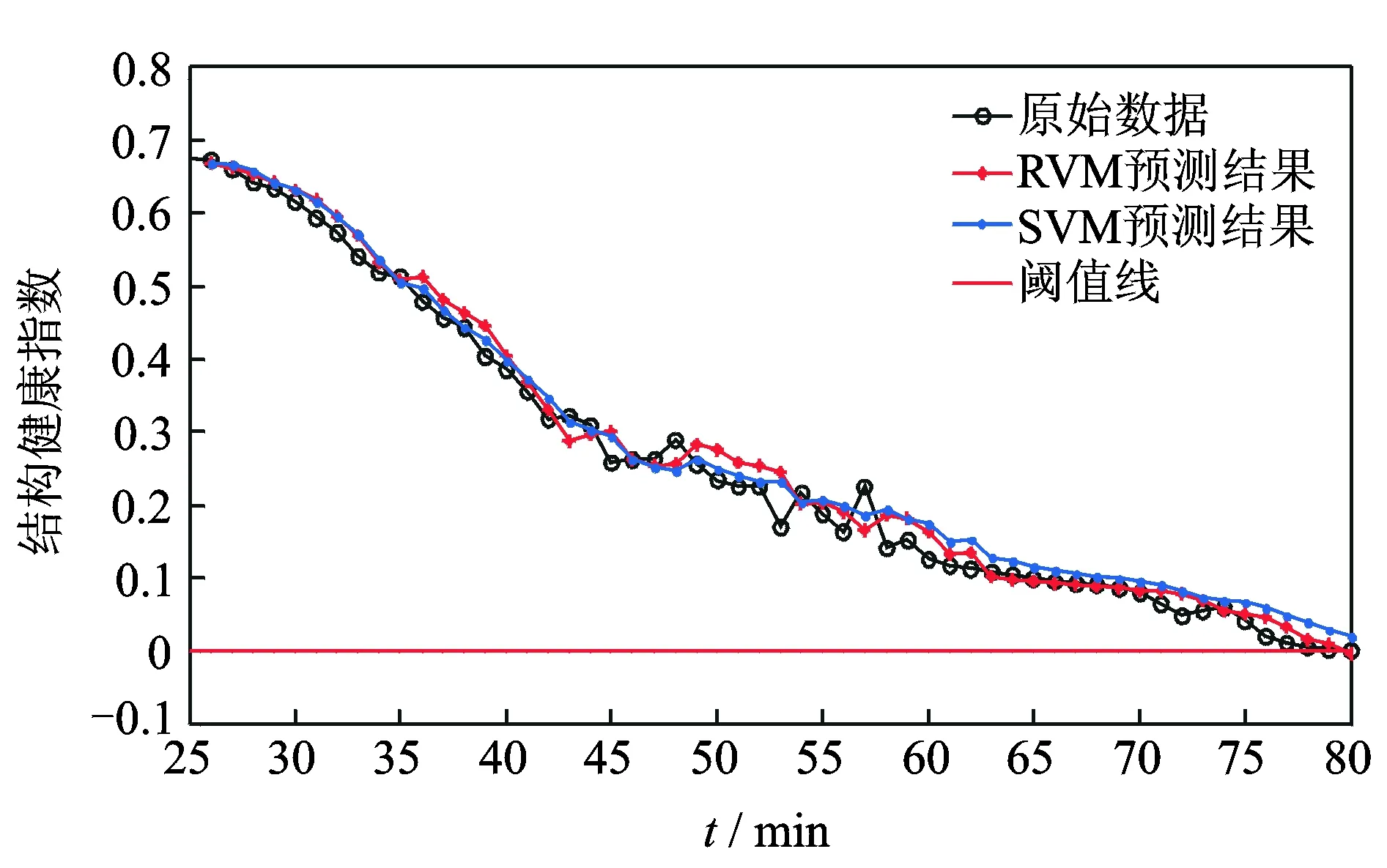
图6 健康状态指数预测结果Fig.6 Prediction results of the health state index

当利用RVM预测第79个结构损伤指数时，得到的结构健康指数为0.009，非常接近0，复合材料试验件出现大约2.7 mm的裂纹。此时，从轻微冲击损伤试验件进行加速试验开始到出现裂纹2.7 mm的时间间隔为79 min，而试验带有轻微损伤的复合材料试验件从试验开始到出现裂纹的时间间隔为80 min，其结构健康状态预测结果的平均相对误差为1.23%。

从图6可以看出，由SVM模型预测的结果有一定的滞后性，并且SVM模型预测到第80分钟时结构健康指数值为0.021，而RVM模型预测到第80 min时结构健康指数值为-0.04，说明SVM明显滞后于RVM模型的预测结果，说明了RVM模型预测的有效性。

4 结论

1) 提出了基于LTSA的多特征降维融合方法，结合不同传感器的各自特征信息，通过降维融合可以很好地表征出复合材料结构健康特性，克服了单一传感器表征复合材料结构健康特性的局限性，使复合材料结构健康特性的表征更符合实际要求。

2) 创建的基于RVM复合材料结构损伤演化与预测模型，预测准确性高，能很好地实现复合材料结构损伤预测效能，对飞机复合材料结构损伤预测起到很好的技术指导，具有较好的实际使用价值。

[1] 马保全,周正干.航空航天复合材料结构非接触无损检测技术的进展及发展趋势[J].航空学报,2014,32(7):1787-1803.

Ma Baoquan, Zhou Zhenggan.Progress and development trends of composite structure evaluation using noncontact nondestructive testing techniques in aviation and aerospace industries[J]. Acta Aeronautica et Astronautica Sinica,2014,32(7):1787-1803. (in Chinese)

[2] 谢宗蕻,刘海涵,张子龙.层间增韧复合材料层合板低速冲击损伤预测[J].南京航空航天大学学报，2013,45(5):686-692.

Xie Zonghong, Liu Haihan, Zhang Zilong. Prediction on low velocity impact damage of interlayer-toughened composite laminate[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013,45(5):686-692. (in Chinese)

[3] 孙中雷,赵美英,姚辽军.胶接修补复合材料层合板的渐进损伤分析方法[J].西北工业大学学报，2013,31(1):83-88．

Sun Zhonglei, Zhao Meiying, Yao Liaojun. An effective progressive damage analysis method failure analysis of composite scarf joint[J]. Journal of Northwestern Polytechnical University, 2013,31(1):83-88. (in Chinese)

[4] 马存旺,鲁国富,李光亮.整体复合材料结构分层疲劳全寿命预测方法研究[J].计算力学学报，2013,30(3):454-460.

Ma Cunwang, Lu Guofu, Li Guangliang. Study on prediction method for delamination fatigue total lives of integrated composite structures[J]. Chinese Journal of Computational Mechanics, 2013,30(3):454-460. (in Chinese)

[5] 张熠卓,徐光华,梁霖,等.利用增量式非线性流形学习的状态监测方法[J].西安交通大学学报,2011,45(1):64-68.

Zhang Yizhuo, Xu Guanghua,Liang Lin, et al. Condition monitoring method for mechanical equipments based on incremental nonlinear manifold learning[J]. Journal of Xi′an Jiaotong University,2011,45(1):64-68. (in Chinese)

[6] 孙志刚,翟玮星,李伟伦,等.基于EMD和相关向量机的短期负荷预测[J].电力系统及其自动化学报,2011,23(1):92-97.

Sun Zhigang, Zhai Weixing, Li Weilun, et al. Shortterm load forecasting based on EMD and RVM[J]. Proceedings of the Chinese Society of Universities for Electric Power System and Automation, 2011,23(1):92-97. (in Chinese)

[7] 杨庆,陈桂明,何庆飞，等.局部切空间排列算法用于轴承早期故障诊断[J].振动、测试与诊断,2012,32(5):831-835.

Yang Qing, Cheng Guiming, He Qingfei, et al. Inchoate faultdiagnosis of rolling bearings based onlocaltangent space alignmentalgorithm[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(5):831-835. (in Chinese)

[8] 盛艳燕,胡志忠.基于小波和马氏距离的电力电子电路故障诊断[J].电子测量技术，2013,36(2):108-112.

Sheng Yanyan,Hu Zhizhong.Fault diagnosis of power electronic circuit based on wavelet and mahalanobis distance[J].Electronic Measurement Technology, 2013,36(2):108-112. (in Chinese)

[9] 张梅军,陈灏,曹勤,等.基于SVM信号延拓改进的EEMD方法[J].振动、测试与诊断,2013,33(1):93-98.

Zhang Meijun, Chen Hao, Cao Qing, et al. The improved EEMD method based on SVM signal continuation[J]. Journal of Vibration, Measurement & Diagnosis,2013,33(1):93-98. (in Chinese)

[10]范庚,马登武.基于EMD和RVM-AR的航空发动机磨损故障预测模型[J].计算机测量与控制,2013,21(7):1746-1749.

Fan Geng, Ma Dengwu. Aero-engine wear faults prediction based on EMD and RVM-AR[J]. Computer Measurement & Control,2013,21(7):1746-1749. (in Chinese)

[11]王醇涛,陆金铭.运用HHT边际谱的柴油机故障诊断[J].振动、测试与诊断,2010,33(4):465-468.

Wang Chuntao, Lu Jinming. Fault diagnosis of diesel engine based on HHT marginal spectrum[J]. Journal of Vibration, Measurement & Diagnosis,2010,33(4):465-468. (in Chinese)

[12]Tipping M E. Sparse Bayesian learning and the relevance vector machine[J]. Journal of Machine Learning Research, 2011,1(3):211-244.