基于星载测向系统的干涉仪安装角校正方法

李廷军+刘磊+王威+张海波+林瑜

摘 要：在对单星干涉仪测向定位系统中，针对干涉仪基线安装角存在系统误差的问题，文中提出了一种干涉仪基线安装角非线性模型估计方法，将干涉仪的相位差观测量与基线安装角系统误差间的非线性关系在观测值处进行线性化处理，通过多次迭代，求出安装角系统误差估计值。最后仿真分析了安装角系统误差估计方法的定位性能。

关键词：测向；安装角；标校；误差估计

中图分类号：TP272；O24 文献标识码：A 文章编号：2095-1302（2017）02-00-04

0 引 言

在单星瞬时测向定位过程中，影响测向定位精度的因素较多。定位系统不仅会在定位滤波算法方面存在偏差[1，2]，影响定位精度，也会在观测卫星相关参数（如卫星上的干涉仪相位差测量误差、干涉仪安装角误差、卫星姿态误差、卫星位置误差，频率测量误差等）的测量方面不可避免地存在一些误差，从而导致目标参数（目标的俯仰角，方位角，目标辐射源信号频率等）出现测量误差，影响定位精度[3-8]。因此，要提高定位精度，需要对卫星观测参数误差进行必要的标校，以提高获取的测量参数的准确性[9]。

本文主要以二维相位干涉仪测向系统安装角误差对测向定位精度的影响为出发点，提出了一种干涉仪基线安装角非线性模型估计方法[10]。首先将相位差测量方程在测量处线性化，利用高斯-牛顿（Gauss-Newton）法[11]多次迭代求得基线安装角误差，通过校正定位后，可有效提高干涉仪测向定位精度。最后分析了系统安装角误差估计方法的克拉美-罗下限（Cramer Rao Low Bound， CRLB），并将其与仿真的测向误差均方根误差进行了对比。

1 安装角误差建模

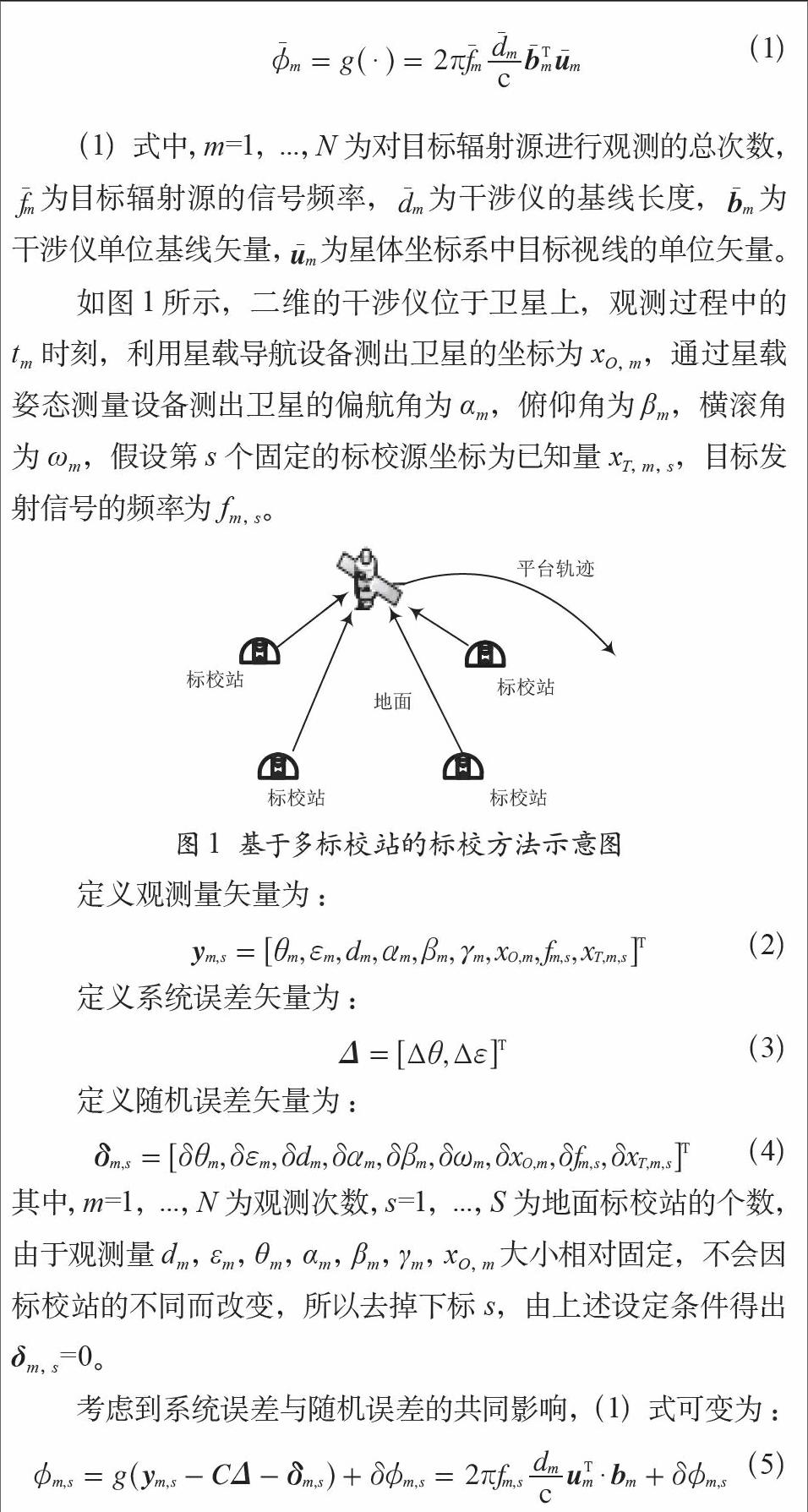
基于多标校站的标校方法示意图如图1所示。地面上的多个标校站和卫星构成观测标校模型[12]。通过地面标校站发射一定频率的信号，星载导航设备接收到信号后，测量并计算出辐射源来波到达两天线的模糊相位差，对相位差解模糊后得到无模糊相位差，再利用先验信息（标校站的位置为已知量）估计出干涉仪基线的安装角系统误差。

系统误差估计的流程如下所示：

（1）假设系统误差Δ的初始值为0；

（2）用ym，s+CΔ替换观测量ym，s；

（3）利用ym，s和φm，s计算出z和B；

（4）利用最小二乘法算出系统误差的估计值；

（5）预先设置好门限值，将与门限值进行比较，或者将最大迭代次数和已进行的迭代次数比较，据此判断迭代是否满足收敛条件。如果比较结果能够满足条件，则进入下一步骤；如果比较结果不满足条件，则令转入步骤（2）中再次迭代计算；

（6）将作为系统误差Δ的最终估计结果。

2.2 CRLB计算

推导在无模糊相位差条件下，系统误差估计Δ的克拉美罗下限CRLB，将CRLB用于衡量系统误差估计算法的性能。

3 测向修正计算方法及仿真分析

3.1 测向校正计算方法

下面分析二维相位干涉仪基线安装角线性模型的校正计算方法。如图2所示，在平台坐标系下，三根测量天线按照相互之间正交的方式，组成了二维干涉仪，假设对目标方位方向的基线矢量为ba，俯仰方向的基线矢量为bb，目标视线方向的单位矢量为，采用如上所述的方法分别求各自的系统误差Δba，Δbb之后，就能够对系统误差进行校正。

其中，为测向过程中单次定位的仿真结果，M为蒙特卡洛仿真次数，并且取M=10 000次进行仿真。

假设卫星初始坐标点为O（0，0，10 000）m，速度矢量为（500，0，0）m/s，朝x轴的正向匀速运动。三个标校源的载频大小依次为：5.1 G，5.12 G，5.14 G，标校源的坐标依次為： A1（8 000，-1 500，0）m，A2（6 000，2 500，0）m，A3（8 500，1 000，0）m，目标坐标S（9 000，4 500，0）m，载频为5.4 G。假设卫星共进行80次观测，观测的时间间隔为1 s，观测时长共为80 s。观测天线依照正交的方式构成十字形干涉仪，假设干涉仪俯仰基线长度与方位基线长度均为1.3 m。进行观测的场景示意图如图3所示。

仿真1：系统误差估计性能

如图3所示，卫星从O点出发，以500 m/s的速度朝x轴的正向飞行，每间隔1 s对相位差进行一次数据采集，A1，A2，A3这三个标校源同时进行80次观测，共计240个脉冲。设定系统误差值Δθ=Δε=0.15°。

图4所示为在白色高斯噪声的背景下，当相位差的测量误差处于5～70°的大小区间变化时，方位基线的系统误差定位性能，并分别用RMSE（Δφ），RMSE（Δθ），RMSE（Δε）来表示。

从图4和5中可以看出，当相位差的测量误差在5～70°的区间变化时，文中提出的安装角非线性模型估计方法均可达到CRLB，充分说明了该算法的有效性。

仿真2：校正后测向定位性能

为了对本文提出方法的有效性进行验证，文中将给出校正前后对目标的测向结果。仿真场景与前述一致，卫星的初始位置、速度矢量、采样模式以及系统误差的设置均保持不变。假设目标点的坐标为S（9 000，4 500，0）m，当卫星经过坐标O2（2 500，0，8 000）m时，对目标辐射源进行一次测向定位。目标点的真实方位角和俯仰角分别为27.9°，38.6°。

图6所示为相位差测量误差处于5～75°区间范围时，对目标的定位结果均方误差曲线。“校正前”指系统误差未经校正得出的定位结果；“只校方位角”指仅对干涉仪基线方位角的系统误差进行校正的定位结果；“只校正俯仰角”指仅对干涉仪基线俯仰角的系统误差进行校正的定位结果；“校正后”指利用本文校正方法同时对干涉仪基线方位安装角和俯仰安装角进行校正的定位结果。

（1）安装角系统误差校正前的定位RMSE误差最大，说明干涉仪安装角的误差对测向定位精度的影响比较大。

（2）只校正俯仰角安装误差时，定位性能比只校正方位安装角误差的定位性能要好，说明在频率5.4 G时，相对方位安装角的系统误差来说，俯仰安装角的系统误差对定位精度的影响更大。

（3）本章提出的安装角误差非线性估计方法性能较好，能够大大减弱测向过程中系统误差的影响程度，提高测向定位精度；

（4）当相位差测量误差≥45°时，“只校正俯仰角”和“校正后”两者的定位性能比较接近，表明当相位差测量误差很大时，基线方位安装角系统误差对测向定位精度的影响比较小，可以不考虑。

4 结 语

本文针对二维相位干涉仪测向定位过程当中，干涉仪基线安装角存在系统误差使定位精度降低的问题，提出了一种基于多标校站的基线安装角非线性模型估计方法，通过在观测值处，将相位干涉仪的相位差观测量和基线安装角系统误差二者之间的非线性关系进行线性化处理，并经过多次高斯-牛顿（Gauss-Newton）法迭代，求出基线安装角系统误差估计值，通过理论分析和仿真分析表明，该方法能达到克拉美罗下限（CRLB），可有效消除二维相位干涉仪测向定位中系统的基线安装角系统误差，提高测向定位精度。

参考文献

[1]刘海军，柳征，姜文利，等.基于星载测向体制的辐射源定位融合算法[J].系统工程与电子技术，2009， 31（12）： 2875-2878.

[2]田明辉，方青，钮俊清.星载平台地面目标测向定位仿真研究[J].雷达科学与技术，2012，10（3）：262-266.

[3]李腾，郭福成，姜文利.星载干涉仪无源定位新方法及其误差分析[J].国防科技大学学报，2012，34（3）：164-170.

[4]王强.基于干涉仪体制的运动单平台无源定位技术研究[D].长沙： 国防科学技术大学，2010.

[5]吴宝东，陈舒.基于相位干涉仪测向系统的相位误差分析[J].舰船电子对抗，2008（6）：74-76.

[6]张文旭，司锡才，蒋伊琳.相位干涉仪测向系统相位误差研究[J].系統工程与电子技术，2006，28（11）：164-170.

[7]陆安南.对电子侦察卫星无源定位技术发展问题的思考[J].通信对抗，2008，100（1）：15-20.

[8]徐义.基于多普勒信息的单星无源定位新技术研究[D].长沙：国防科学技术大学，2009.

[9] Kazufumi Ito，Kaiqi Xiong. Gaussian Filters for Nonlinear Filtering Problems[J].IEEE Transactions On Atuomatic Control， MAY 1999，4（5）：910-927.

[10]杨争斌，钟丹星，郭福成，等.一种基于高斯牛顿迭代的单站无源定位算法[J].系统工程与电子技术，2007， 29（12）：2006-2009.

[11]钟丹星，杨争斌，周一宇，等.LBI测向定位系统的多标校源校正算法[J].系统工程与电子技术，2008，30（5）：960-963.

[12]罗贤欣，刘光斌，王忠.干涉仪测向技术研究[J].舰船电子工程，2012，32（8）：74-76.