基于入侵杂草优化算法的支持向量机负荷预测

周尚珺玺，马立新

( 上海理工大学 光电信息与计算机工程学院，上海200093)

基于入侵杂草优化算法的支持向量机负荷预测

周尚珺玺，马立新

( 上海理工大学 光电信息与计算机工程学院，上海200093)

针对支持向量机(Support Vector Machine, SVM)预测方法中的参数选取主要依靠经验试算实验比对的方法导致难以快速选择合适参数从而影响负荷预测精度的问题，研究了将入侵杂草优化算法(Invasive Weed Optimization，IWO)与支持向量机算法相结合的改进算法。提出控制误差ε的取值，采用入侵杂草寻优算法对惩罚参数C和核函数参数σ进行优化选取，将自动寻优的结果赋给支持向量机，从而实现支持向量机自动寻优。用某市的历史负荷及相关天气等信息数据，通过仿真实验证明了IWO-SVM算法用于短期负荷预测的可行性，以及IWO算法对改善SVM的参数选择的有效性。平均预测误差在3%以内，满足行业要求。

短期负荷预测；支持向量机；入侵杂草优化

0 引言

电力系统短期负荷预测是维护电网经济、稳定运行的基础，是制订供电计划、调度计划和交易计划的重要依据，基于人工智能技术的神经网络预测模型和模糊系统预测模型是目前研究较为广泛的负荷预测模型，但对改善这类模型的泛化能力方面理论进展较慢，因此很多学者开始对具有更好泛化能力的预测技术进行研究。

由 Vanpik 在1995年提出的建立在统计学习理论的VC维理论和结构风险最小原理的基础上发展出的支持向量机方法，它在解决小样本、非线性、高维数模式识别等实际问题中有许多优势。支持向量机方法是根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折中，以获得最好的泛化能力。近年来基于支持向量机的负荷预测方法被重点关注，文献[1]全面总结了支持向量机在短期负荷预测中的应用情况，对比了常用的人工神经网络预测方法，从原理上证明了支持向量机方法的优越性。

在对支持向量机预测方法的研究中发现，该方法的预测性能主要依赖于模型中的参数选择，而目前对于模型中的参数选择主要依靠经验或通过大量实验比对给定，文献[2]提出的参数选取方法大多采用交叉验证(Cross Validation, CV)的方法或凭借经验给出，总体上具有一定的盲目性，不容易找到函数全局最优值，达不到预期的精度和满意的效果。因此为了提高支持向量机方法的预测性能，其参数选择及优化成为了研究的新方向，文献[3]介绍了支持向量机模型的传统参数选取方法及优化方法，并在此基础上提出了基于高斯核函数的参数选取及优化方法，避免了基于交叉检验的试探法的盲目性，提高了建模效率。文献[4-6]分别提出了基于粒子群、遗传算法优化算法的模型参数选择方法，克服了传统参数选择的缺点，较大地提高了支持向量机的寻优能力，但粒子群容易陷入局部最优解，遗传算法收敛速度较慢等问题都有待改进。

本文针对SVM传统的参数选取方法效率较低、影响性能等缺陷，将入侵杂草算法用于支持向量机参数的选取，提出控制误差ε的取值，采用入侵杂草寻优算法对惩罚参数C和核函数参数σ进行优化选取。入侵杂草算法收敛速度大于粒子群、遗传算法等，采用子父代竞争排斥机制，避免早熟与陷入局部最优解，该方法将入侵杂草算法自动寻优的结果赋给支持向量机，提高了支持向量机预测精度，为优化支持向量机参数提供了一种新方法。

1 回归支持向量机

支持向量机是基于SRM和VC维理论的一种训练机器学习的算法，其核心包括：(1)通过非线性映射，将低维空间中线性不可分的样本映射到高维空间中[7]，该空间中存在能将样本的非线性特征进行分割的超平面；(2)基于架构风险最小化原则，寻找一个最优超平面，使得该超平面到不同类的数据点的间隔最大。

支持向量机回归理论是建立在支持向量机分类问题的基础上的，通过引入不敏感损失函数ε，将支持向量机分类理论中的结果推广，使其用于函数回归。

设有训练样本：{xi,di},(i=1,...,n,xi∈Rn,di∈R)。x是输入向量，d是期望值，采用回归函数：

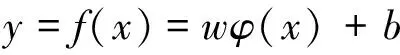
式中：φ(x)是从输入空间映射到高为特征空间的非线性函数。

系数w,b由最小化下式来估计：

(1)

(2)

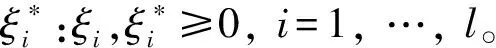
此时最小化问题为：

(3)

约束条件为：

(4)

由于特征空间维数较高，甚至到无穷维，所以直接求解并不现实，回归支持向量机通过建立核函数k(xi,xj)来解决维数灾难。

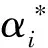
(5)

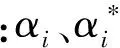
(6)

对拉格朗日函数式求偏导可解得：

(7)

将w表达式代入得：

(8)

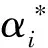
根据KKT条件，在最优处满足拉格朗日乘子与约束式的乘积为零，故有：

(9)

求解可得：

(10)

用支持向量便可求解出b的值，求解出回归函数。

2 入侵杂草优化算法

2.1 杂草特性

大自然中杂草是以细胞繁殖生成种子，通过风、水及动物等形式携带种子随机的散布在田地内，田地里的资源分别被每个种子独立的使用，并找到合适自己生长的机会空间。由于杂草的生长和繁殖受土地的肥沃营养程度、杂草的聚集密度和杂草群对环境适应性的影响，在杂草繁殖进化的过程中，能更好适应周围环境的种子会使用更多的土地资源和营养，并能更好更快的成长，结籽(种子)更多，不能很好地适应环境的种子，在长成为植株后结籽(种子)较少，因而植株群落对环境的适应性的提高能够让植株的生存能力更顽强，存活的时间更长。植株的自然繁殖进化选择方式多种多样，r选择和k选择尤为重要，r选择即是从植物群落中挑选出生命力旺盛、适应性强、成长快速、枯萎块、竞争力极强的植物，并让它们拥有占据更多的新领地和新环境；k选择即是选择生长和繁殖缓慢、坚韧性强、并让其去占据有限的环境和资源营养空间。r选择就是IWO算法的全局搜索方式，k选择就是IWO算法的局部搜索方式。

2.2 入侵杂草基本理论

入侵杂草优化算法是2006年由Mehrabian和Lucas提出的模拟大自然野草繁殖进化的一种随机搜索仿生学优化算法。该算法具有收敛性好、鲁棒性强、结构简单、易于编程实现等优点。

该算法以适应度为基准的繁殖机制，繁殖过程中按自然界的繁殖法则，给予不可行的个体生存和繁殖的机会以保留更多有用信息；该算法采用正态分布的扩散机制，同时进行全局搜索和局部搜索，使其具有一定深度同时也不失广度，并能根据迭代次数不同对二者强度进行调节，同时采用子父代竞争排斥机制，最大限度保留有用信息，避免早熟和陷入局部最优[8-9]，算法基本步骤：

第一步：种群初始化。确定种群初始化数量N0和最大种群规模Nmax、最大迭代次数itermax等基本参数。

第二步：生长繁殖。 每个杂草种子根据式中适应度(繁殖能力)产生种子，父代杂草产生的种子个数与母体杂草的适应度成正比，适应度越好，种子繁殖数越多：

(11)

式中：f为当前杂草的适应度值；fmax及fmin分别是当前种群中杂草的最大及最小适应度值；smax及smin分别代表一个杂草能产生的最大及最小种子的数量。

第三步：空间分布。 以父代为均值，子代个体以σ为标准差正态分布扩散在父代个体周围。迭代过程中，每一代的标准差按如下规律进行变化：

(12)

式中：iter为当前进化的迭代次数；itermax为最大进化迭代次数；σcur为当前的标准差；σinit和σfinal分别是标准差的初始值和最终值；n为非线性调和因子。该式对于iter是递减的，确定了杂草算法前期是全局搜索为重、后期以局部搜索为重的基本特性。

第四步：竞争淘汰。 经过数代的繁殖后，产生的后代杂草和种子数目将达到预先设定的最大种群数目，然后将父代和子代一起进行排列，按适应值大小进行优胜劣汰。

第五步：重复步骤直至满足设定的最优解条件或达到最大迭代次数。

3 入侵杂草-支持向量机模型

入侵杂草-支持向量机是使用入侵杂草优化算法求解支持向量机的参数，解决选择支持向量机参数选择没有理论依据可循的问题，提高支持向量机的学习和推广能力。用入侵杂草优化算法优化支持向量机的核心思想是：将参数选择问题视为杂草种群在给定空间的全局搜索问题，入侵杂草优化算法将支持向量机的参数(C,σ)看作是杂草和种子的适应度值，将测试样本集的平均误差作为算法结束的判断条件，实现支持向量机参数的自动优化选取。具体的算法流程图如图1所示。

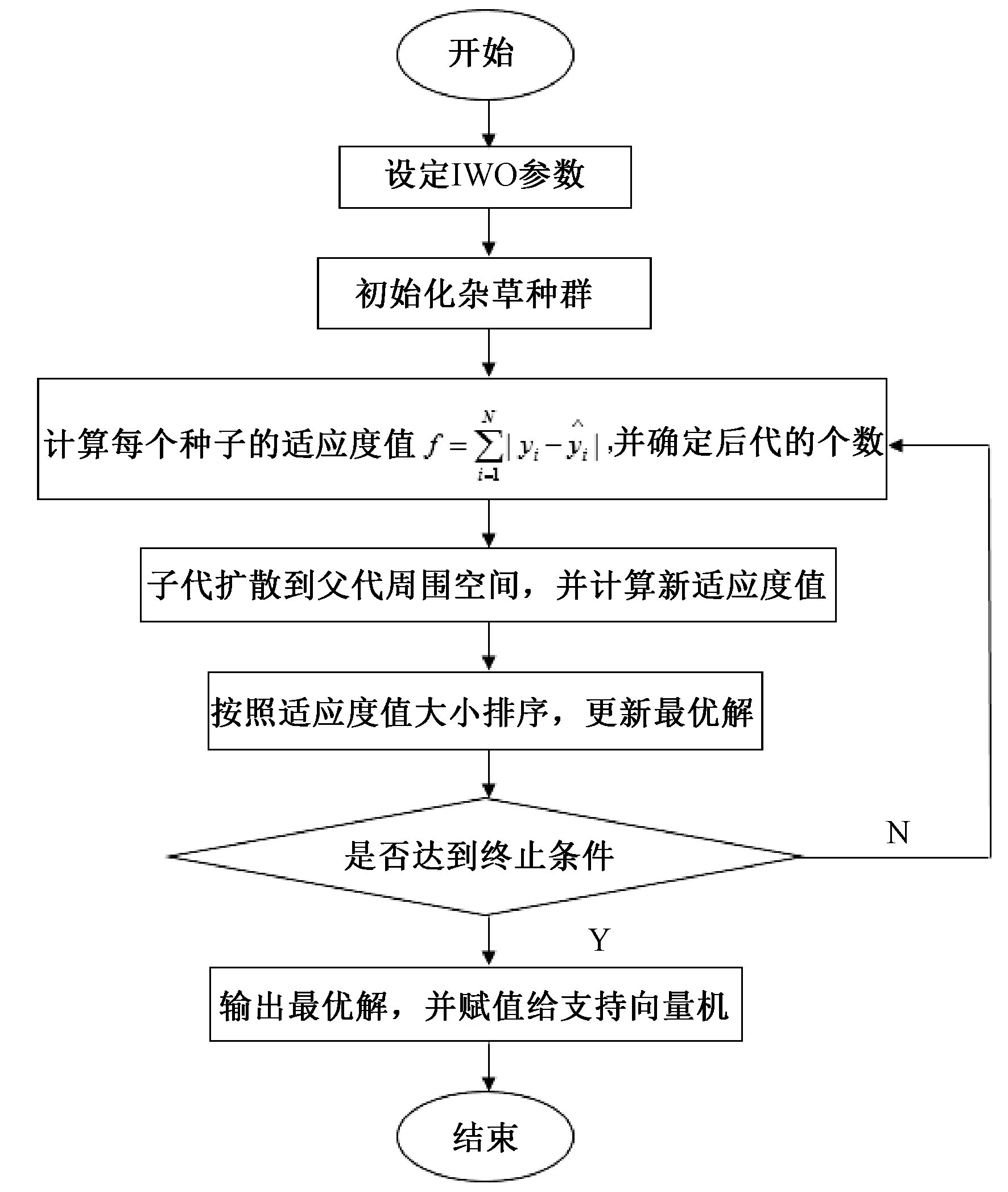
图1 入侵杂草-支持向量机算法步骤

4 算例分析

4.1 输入样本选取

文献[10]对电力负荷周期性的分析可知，预测日前1周及前几天同一时刻的负荷数据与待预测时刻的负荷关联度较高,而天气因素中温度对短期负荷的影响最大，因此，将预测日前一周与前一日的邻近时刻负荷数据、温度数据及相关日类型作为参考影响因子，将其作为输入对算法进行学习，可得到更准确地预测结果。

为预测1天从0点到23点的实际负荷，分别建立如下的单点负荷预测模型，支持向量机模型输入量共16个，具体选择如表1所示。

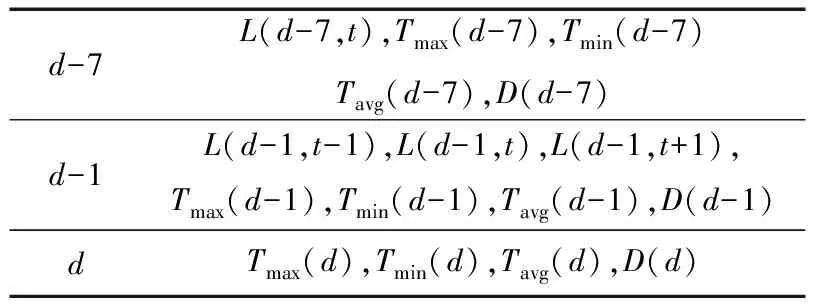
表1 支持向量机模型输入量

其中，d代表待预测日，d-1、d-7分别代表待预测日前一天和前一周；L(d-7,t)代表d天t时刻的历史负荷值；Tmax(d)、Tmin(d)、Tavg(d)分别表示d天最高温度、最低温度、平均温度；D(d)代表d天日类型。

输出量L(d,t)为d日t时刻的负荷预测值。把预测日前30 d相应的历史负荷数据、气象信息和日类型因子作为训练样本。

4.2 模型参数选择

支持向量机核函数选择RBF函数，杂草入侵优化算法中种群初始化数量：20个；最大种群规模：30个；最大迭代次数：150次；生成种子数量上下限：20-0个；非线性指数：3；问题维数：2；标准差初始值：1；标准差最终值：0.001。

4.3 算例结果

采用SVM与IWO-SVM 2种算法，以MATLAB作为仿真平台，以某市2012年7月1日到2012年8月31日每天24点的负荷数据、当地气象因素及对应的日类型作为实验数据，分别对2012年8月25日至31日进行了次日24点的负荷预测。

对于单日24点负荷预测情况选取8月29日为例进行分析，实际负荷曲线与采用SVM方法建立模型的拟合曲线的对比如图2所示。

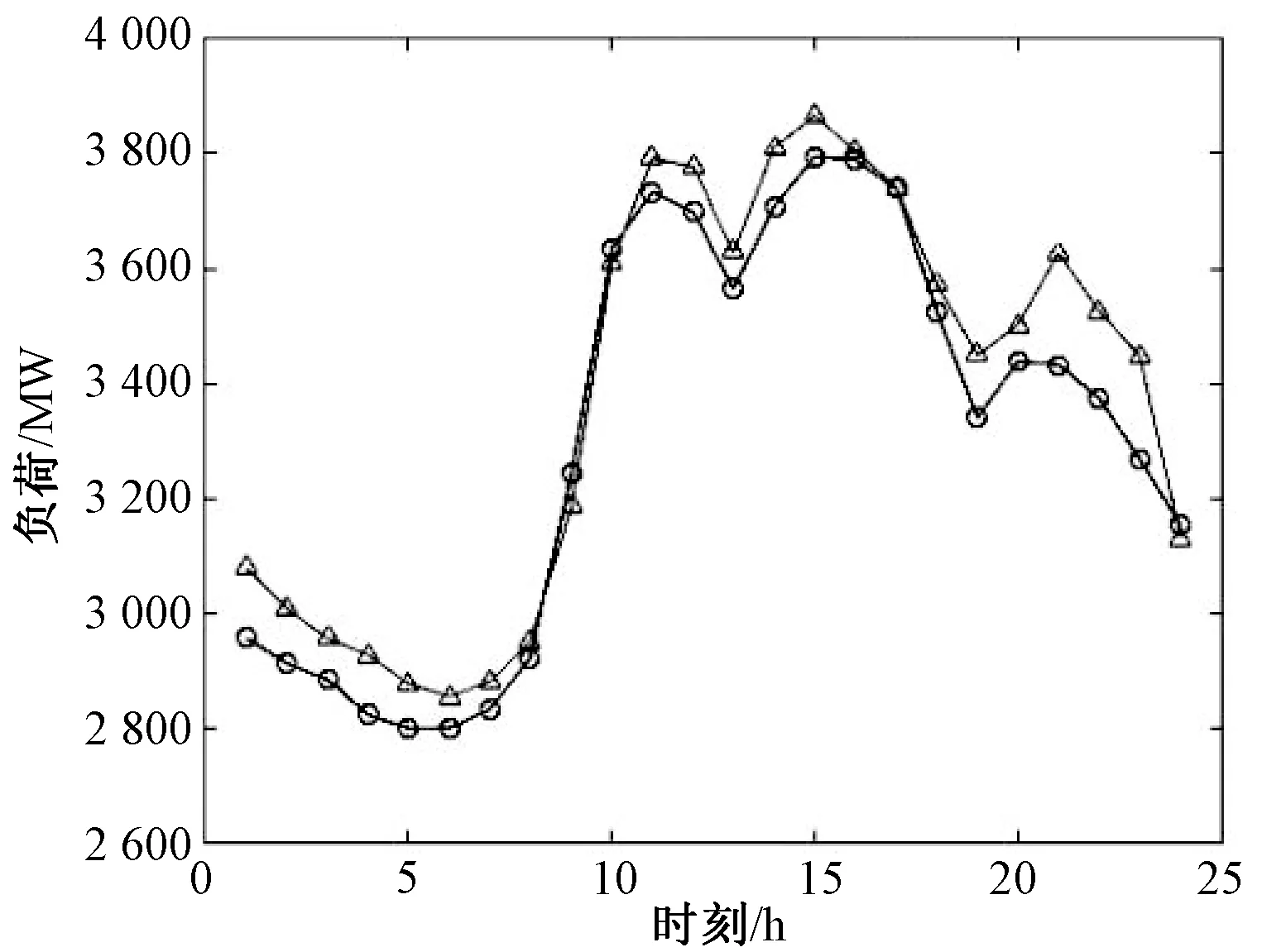
图2 SVM算法负荷曲线对比

其中，带圆圈标记的曲线代表真实负荷，带三角标记的曲线表示SVM预测结果曲线。误差曲线如图3所示。

图3 SVM预测误差曲线

由图2、图3可看出，采用SVM算法的预测结果整体走势基本与真实值相吻合，最小相对误差为0.06%，最大相对误差为5.67%，24点平均相对误差为 2.375%。

采用IWO-SVM模型进行的单日24点负荷预测情况如表2。

表2 8月27日24点负荷预测

续表2

由表2中数据可看出，采用IWO-SVM算法的预测结果与真实值非常接近，最小相对误差为0.469%，且预测误差超过3%的点只有2个，最大相对误差为3.416%，24点平均相对误差为1.701%，比SVM算法的精度和稳定性都更好。

采用2种方法对1周7天的负荷进行了预测，每天的平均误差结果如表3所示。

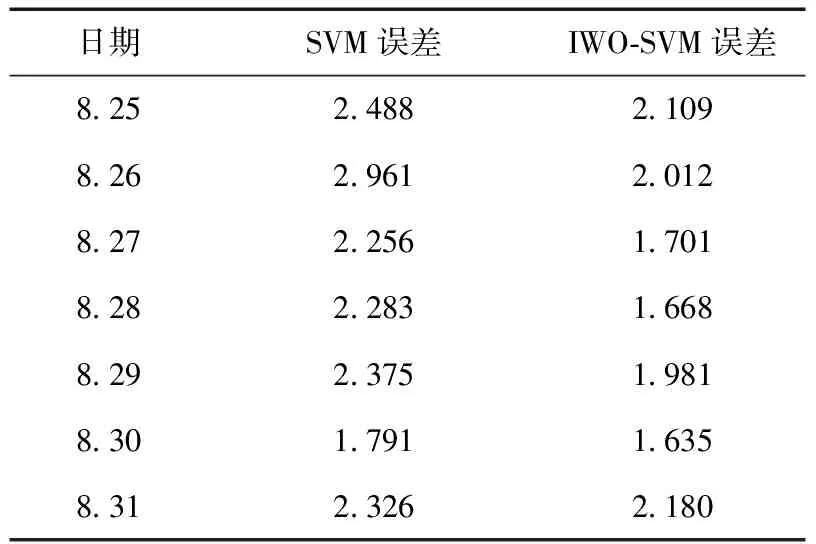
表3 SVM与IWO-SWM算法预测误差

由表3可知，SVM和IWO-SVM算法预测的准确度均达到97%，满足调度部门对于日负荷预测准确率的要求，也说明了2种算法在实际应用中的可行性。比较SVM 与IWO-SVM 2种方法的实验结果：SVM的预测结果不够稳定。而IWO-SVM的预测结果误差相对稳定且预测误差更小。实验结果表明：IWO-SVM模型的预测较SVM方法有更高的准确度，证明了IWO寻优算法优化SVM的参数选择的可行性。

5 结论

本文针对SVM传统的参数选取主要依靠经验试算实验比对的方法导致难以快速选择合适参数从而影响负荷预测精度的问题，研究了将入侵杂草优化算法与支持向量机相结合的改进算法。提出控制误差ε的取值，采用入侵杂草寻优算法对惩罚参数C和核函数参数σ进行优化选取，将自动寻优的结果赋给支持向量机，实现支持向量机自动寻优。通过MATLAB仿真实验，算例结果表明，入侵杂草算法提高了支持向量机预测精度，有效优化了模型参数，提高模型预测性能。

[1]王奔，冷北雪，张喜海，等.支持向量机在短期负荷预测中的应用概况[J].电力系统及其自动化学报，2011，23(4)：115-121.

[2]张倩, 杨耀权. 基于支持向量机核函数的研究[J]. 电力科学与工程，2012，28(5)：42-45.

[3]谢宏，魏江平，刘鹤立.短期负荷预测中支持向量机模型的参数选取和优化方法[J].中国电机工程学报，2006，26(22)：17-22.

[4]谷文成，柴宝仁，滕艳平.基于粒子群优化算法的支持向量机研究[J].北京理工大学学报，2014，34(7)：705-709.

[5]王琼瑶，何友全，彭小玲.基于改进遗传算法的支持向量机参数优化方法[J].计算机与现代化，2015(3)：33-36.

[6]郭克友，郭晓丽，王艺伟，等.SVM参数优化方法分析与决策[J].计算机测量与控制，2016，24(6)：255-259.

[7]曾繁耀，黄昭荣.短期电网负荷预测方法研究[J].自动化与仪器仪表，2016(8)：84-86.

[8]周金虎. 基于入侵杂草算法的数据挖掘聚类算法研究[D].兰州：兰州理工大学，2014.

[9]左旭坤，苏守宝.多子群入侵杂草优化算法研究及应用[J].计算机工程，2014，40(2)：184-188.

[10]马立新，李渊.日最大负荷特性分析及预测方法[J]. 电力系统及其自动化学报，2014，26(10):31-34.

Load Forecasting Based on Support Vector Machine Optimize by Invasive Weed Optimization

ZHOU Shangjunxi， MA Lixin

( School of Optical-Electrical and Computer Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China)

Aiming at the problem of the support vector machine(SVM) parameter selection methods rely mainly on the experience calculation and its low efficiency defects, a new method, invasive weed optimization(IWO) algorithm, combining with SVM, is proposed. By controlling the value of error and using IWO algorithm to optimize the punish parameters and kernel parameters, the model is constructed. As the relevant historical load data, weather data and other information of city of Jiangsu Province used as the simulation data, the simulation results prove the feasibility of the SVM algorithm for short-term load forecasting and the effectiveness of the IWO algorithm for improving the parameters of SVM. The experimental results show that the prediction accuracy of this method can meet the industry requirements, with the average error less than 3%.

load forecasting; support vector machine; invasive weed optimization algorithm

10.3969/j.ISSN.1672-0792.2017.02.006

2016-09-13。

上海张江国家自主创新重点资助项目(201310-PI-B2-008)。

TM715

A

1672-0792(2017)02-0035-06

周尚珺玺(1992-)，女，硕士研究生，研究方向为电力负荷预测及电力营销。

马立新(1960-)，男，教授，主要从事电力系统分析与优化运行，智能电网与智能科学，电气设备状态监测与诊断方法，电能质量监控与能效测评技术，风光发电智能控制系统方面的研究。