基于流固耦合作用的上悬式离心机转鼓解析动力学建模

杨旭娟 徐光恒 李宇龙 李兆军

(1. 广西制造系统与先进制造技术重点实验室，广西 南宁 530004；2. 广西大学机械工程学院，广西 南宁 530004；3. 广西高校临海机械装备设计制造及控制重点实验室培育基地，广西 钦州 535000)

基于流固耦合作用的上悬式离心机转鼓解析动力学建模

杨旭娟1,2,3徐光恒1,2李宇龙1,2,3李兆军1,2,3

(1. 广西制造系统与先进制造技术重点实验室，广西 南宁 530004；2. 广西大学机械工程学院，广西 南宁 530004；3. 广西高校临海机械装备设计制造及控制重点实验室培育基地，广西 钦州 535000)

以上悬式离心机转鼓为研究对象，应用有限单元法将转鼓壁划分为板单元，将糖膏划分为三棱柱单元，充分考虑转鼓和糖膏的流固耦合作用，建立反映转鼓与糖膏流固耦合关系的解析动力学模型，比较转鼓在考虑流固耦合作用下和不考虑流固耦合作用的振动模态，分析流固耦合对转鼓振动模态的影响。研究表明，所建上悬式离心机转鼓解析动力学模型反映了系统参数与其动态性能之间的内在关系。同时，由于考虑系统的流固耦合特性，增加了附加质量矩阵，从而对系统的固有频率产生重要影响，为了避免转鼓系统产生共振现象，确定系统的工作频率范围时，应该考虑流固耦合作用的影响。

上悬式离心机；振动特性；流固耦合；转鼓；解析动力学模型；有限元

上悬式离心机作为制糖企业的核心设备，是一种利用离心力将固体和液体分离的旋转机械设备。在制糖工业中，其主要功能是将蔗糖晶体与糖膏分离。为了提高工作效率，需要提高离心机转速；而随着转速的提高，离心机的振动问题就越发严重，导致事故频发[1-2]。因而深入开展上悬式离心机振动特性的研究对确保制糖设备安全高效运行是十分必要的。

目前，学者们对上悬式离心机转鼓动力学问题进行了广泛的研究。例如，ANGHEL C I[3]对离心机转鼓进行了应力分析，并研究了引起应力集中的决定因素；李建明等[4]运用有限元分析法，采用无量纲理论对锥形转鼓和法兰连接处的应力进行分析；蓝永庭等[5]运用Ansys软件对包含孔结构的离心机转鼓进行强度分析，建立优化数学模型对转鼓结构及工艺设计进行优化；李岩舟等[6]运用Ansys软件对上悬式离心机转鼓在满负荷工况下进行强度分析，并对转鼓壁厚进行优化；蒙文[7]运用Ansys软件采用三维有限元法分析加强箍分布参数、截面参数以及过盈量对转鼓应力的影响；Park等[8]建立了水平旋转转鼓的简化离散有限元模型，并进行了离心机转鼓的动态性能及优化，针对转鼓的填充率、转速、摩擦系数对动态性能的影响做了参数化分析。

学者们多年的研究为上悬式离心机的安全稳定工作起到了非常重要的推动作用。但这些研究多是基于软件对离心机转鼓进行建模和分析，难以反映转鼓动态性能与其结构参数的内在关系。已有的研究均未考虑转鼓和糖膏的流固耦合关系。而流固耦合动力学问题的研究已是很多工程领域的研究热点，如水轮机的流固耦合动力学研究[9]，船体与水的流固耦合振动问题研究[10]，储液容器的流固耦合动力学问题研究等[11]。流体与固体之间的流固耦合作用直接影响系统的动态性能，并最终影响系统的安全、可靠运行。糖膏属于流体，在离心机实际的运行过程中，糖膏和流体之间也存在相互作用的流固耦合作用。因此，有必要建立考虑流固耦合作用的上悬式离心机转鼓解析动力学模型。

本研究拟以上悬式离心机转鼓为研究对象，应用有限元法建立转鼓—糖膏系统的流固耦合解析动力学模型，并在该动力学模型的基础上分析流固耦合作用对转鼓振动模态的影响。

1 考虑流固耦合的上悬式离心机转鼓解析动力学模型

1.1 位移模式

上悬式离心机转鼓壁厚相对于转鼓直径较小，在分析中，将转鼓壁视为薄壳，采用三角形板单元将转鼓壁划分单元，见图1。

图1板单元上任意点沿x方向的位移u(x,y,t)，沿y方向的位移v(x,y,t)，沿z方向的位移w(x,y,t)可分别表示为：

(1)

其中，Nui、Nvi、Nwi为单元型函数。

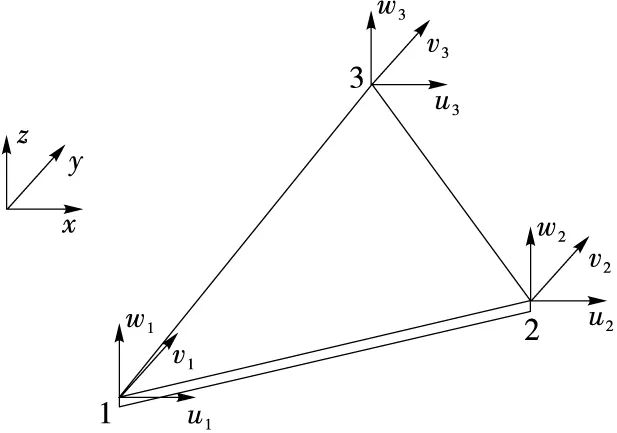
1，2，3表示单元节点，每个节点设u、v、w 3个位移，xyz为单元坐标系

1.2 单元动能

单元的动能可表示为：

(2)

式中：

T——转鼓板单元的动能，J；

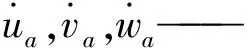
ρ(x,y)——材料质量密度，kg/m3；

h——板壳单元厚度，m。

将式(1)代入式(2)，忽略刚体运动与弹性运动的耦合项，将动能表示成二次型的形式得

(3)

式中：

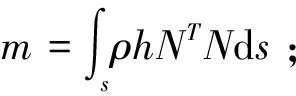
N——转鼓壁板单元形函数矩阵，由转鼓的形状几何参数确定，且

N=

1.3 单元势能

在一般弹性理论中，忽略u、v二阶导数非线性项，而保留一阶导数非线性项，有非线性位移—应变关系：

(4)

将式(1)代入位移—应变关系式(4)，整理得应变与节点位移之间的关系式为：

(5)

式中：

ε ——应变；

S0——应变矩阵，反映了应变与位移之间的关系；

且ε=[εx,εy,γxy]T；

S1=[1,0,0]T,S2=[0,1,0]T,S3=[0,0,1]T；

由应力—应变关系

σ=Dε，

(6)

式中：

σ——应力；

D——弹性矩阵。

式(6)反映了应力与应变之间的关系。

考虑单元的弹性变形能和流体压能，单元的总势能为：

(7)

式中：

p(x,y,z,t)——任意点糖膏流体的压强，Pa；

u——位移向量，u=[u v w]T；

ns——单元表面法向向量。

假设糖膏在转鼓内做定常流动，由计算流体力学，流体域压强分布可表示为：

(8)

式中：

n——流体单元节点数；

NL——流体单元形函数矩阵；

pp——节点压强向量。

由式(1)和式(8)可得：

(9)

式中：

ρf——糖膏质量密度，kg/m3。

根据变分原理，可得流体—结构耦合关系[12]529-531：

(10)

式中：

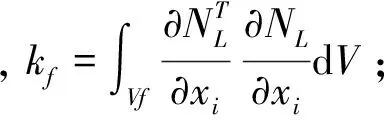
NL——流体单元形函数。

考虑到糖膏厚度比转鼓壁厚度大得多，有一定的厚度，为了与实际情况更为相符，采用6节点线性三棱柱单元将糖膏划分单元，见图2。

为了表示三棱柱单元的型函数，在平行于棱边的方向用坐标ζ，在垂直于棱边的三角平面内用面积坐标Li，且

(11)

式中：

L1,L2,L3——面积坐标。

图2 糖膏三棱柱单元Figure 2 Fillmass three prism unit

将式(5)、(6)和(9)代入式(7)，联立式(10)，并忽略转鼓势能表达式中的几何项后可得转鼓板单元的势能为：

(12)

式中：

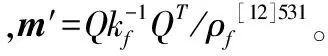
1.4 单元运动微分方程

应用拉格朗日方程：

(13)

式中：

F——外加载荷的广义力向量；

q——转鼓单元受到的与其相联结的单元对其的作用力向量。

得到不考虑阻尼情况下单元的运动微分方程为：

(14)

式中：

1.5 总体方程

将转鼓系统沿周向等分为8个部分，其中每个部分的单元划分见图3，每个部分转鼓壁由4个三角形板单元组成(单元节点为9，10，17，18，25，26)，下底板(单元节点为1，2，9，10)和上挡液板(单元节点为25，26，33，34)分别由两个三角形板单元组成，糖膏由4个三棱柱单元组成(单元节点编号为1，2，9，10，17，18，25，26，33，34，41，42)。

设B为转鼓单元局部编号与系统编号间的坐标协调矩阵，R为转鼓单元坐标与整体坐标间的转换矩阵。采用粘滞阻尼理论来近似估计阻尼的影响，以整体进行编号的转鼓系统广义坐标向量为U，则转鼓系统的运动微分方程为：

(15)

式中：

图3 转鼓有限元模型Figure 3 The finite element model of the drum

M、C、K——分别为转鼓系统的质量矩阵，阻尼矩阵和刚度矩阵；

F——广义力向量；

M0——转鼓壁质量矩阵；

且M=BTRT(m+m′)RB，M0=BTRTmRB，K=BTRTkRB。

从方程(15)的推导过程可见，其中K包含系统的结构参数，M包含转鼓壁质量矩阵和考虑糖膏流体产生的附件质量矩阵，不仅包含转鼓的材料密度和转鼓的结构参数，还包含流体的密度和流体的结构参数等，该解析动力学方程不仅反映了系统动态性能与其系统参数之间的内在关系，还反映了系统的流固耦合特性。

1.6 模态分析

模态分析反映的是系统的固有特性，在方程(15)的基础上，不考虑系统的阻尼和激励，可得上悬式离心机转鼓系统的无阻尼自由振动的动力学方程为：

(16)

假设系统做同步简谐运动，则其解可表示为：

U=Asin(ωt+φ)，

(17)

式中：

ω——系统的固有频率，rad/s；

A——系统的模态矢量。

将式(17)带入式(16)，根据可解性条件，可得系统的频率方程为：

(18)

通过求解方程(18)即可得到系统各阶的固有频率。

2 实例分析

以某大型上悬式离心机转鼓为研究对象，主要结构参数、材料参数及离心机工作参数见表1，将这些参数带入到刚度矩阵和质量矩阵的计算中可得刚度矩阵和质量矩阵，通过求解方程(18)即可得到系统各阶固有频率。进而通过仿真计算可得流固耦合作用对转鼓系统固有频率的影响。

表2为转鼓系统在考虑流固耦合作用下和不考虑流固耦合作用下的前8阶固有频率计算结果，其中η为糖膏流固耦合作用对转鼓固有频率的影响系数，且

η=fs/fa，

(19)

式中：

fa——转鼓不考虑流固耦合作用下的固有频率，Hz；

fs——转鼓考虑流固耦合作用的固有频率，Hz。

由表2可知，考虑转鼓和糖膏的流固耦合作用将使系统的固有频率显著下降，由转鼓系统在流固耦合作用下与不考虑流固耦合作用的前8阶固有频率比较可知，工作状态下，系统在流固耦合作用下的固有频率较小，且流固耦合作用的影响系数为0.7左右。因此，为了避免转鼓系统产生共振现象，确定系统的工作频率范围时，应该考虑流固耦合作用对系统固有频率的影响。

3 结论

本研究建立了上悬式离心机流固耦合解析动力学模型，该模型不仅包含系统的结构参数，而且还包含系统的流体参数，不仅反映了系统动态性能与其系统参数之间的内在关系，还反映了系统的流固耦合特性。由于考虑系统的流固耦合特性，系统增加了附加质量矩阵。系统的前8阶固有频率较不考虑流固耦合作用时均有下降，最大降幅将近30%，可见考虑流固耦合特性对系统的振动模态有重要影响。这将为进一步研究系统的动态性能和优化设计提供依据。

表1 离心机参数表Table 1 Parameters of the centrifuge

表2 转鼓系统前8阶固有频率Table 2 Natural frequencies of the drum

[1] 汤新文, 陈海辉. 离心机转鼓爆裂事故分析[J]. 机电工程技术, 2005, 34(3): 104-105.

[2] MATEO A, HEREDERO F, FARGAS G. Failure investigation of a centrifuge deplex stainless steel basket[J]. Engineering Failure Analysis, 2011, 18: 2 165-2 178.

[3] ANGHEL C I. Stress concentration and fatigue life prediction for disks centrifugal separators[J]. Periodica Polytechnica: Chemical Engineering, 1999, 43(2): 117-136.

[4] 李建明, 薛小平, 唐宗红. 离心机锥形转鼓与法兰连接处应力的有限元分析[J]. 四川大学学报: 工程科学版, 2015, 47(6): 191-197.

[5] 蓝永庭, 陈渊, 张焕, 等. 带加强箍糖用离心机转鼓强度分析及优化设计[J]. 食品与机械, 2014, 30(3): 76-78.

[6] 李岩舟, 陈渊, 王伟, 等. 上悬式制糖离心机转鼓壁厚优化[J]. 机械设计与制造, 2013(9): 178-180.

[7] 蒙文. 加强箍参数对锥篮离心机转鼓应力的影响[J]. 食品与机械, 2014, 30(1): 100-103, 113.

[8] PARK J, WASSGREN C R. Modeling the dynamics of fabric in a rotating horizontal drum using the discrete element method[J]. Particulate Science and Technology, 2003, 21(2): 157-175.

[9] TRIVEDIA C, CERVANTESA M J. Fluid-structure interactions in Francis turbines: A perspective review[J].Renewable and Sustainable Energy Reviews, 2017, 68: 87-101.

[10] 周海波, 蔡少俊, 计方, 等. 流体域特性对流固耦合振动计算的影响[J]. 舰船科学技术, 2015, 37(4): 19-23.

[11] XING Jing-tang. Developments of numerical methods for linear and nonlinear fluid-solid interaction dynamics with applications[J]. Advances in Mechanics, 2016, 46: 95-137.

[12] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.

Analytical dynamic modeling of a top-suspended centrifuge drum with consideration of Fluid-Structure Interaction

YANG Xu-juan1,2,3XUGuang-heng1,2LIYu-long1,2,3LIZhao-jun1,2,3

(1.GuangxiKeyLaboratoryofManufacturingSystem&AdvancedManufacturingTechnology,Nanning,Guangxi530004,China; 2.SchoolofMechanicalEngineering,GuangxiUniversity,Nanning,Guangxi530004,China; 3.GuangxiCollegesandUniversitiesKeyLaboratoryBreedingBaseofCoastalMechanicalEquipmentDesign,ManufacturingandControl,QinzhouUniversity,Qinzhou,Guangxi535000,China)

A top-suspended centrifuge drum was studied with consideration of fluid-structure interaction of the drum and massecuite. The analytical dynamic model was built by finite element method, and a triangle plate element was used to build the basket wall. Moreover, the triangular prism element of six nodes was also utilized to build the massecuite. Therefore, the natural frequencies with and without consideration of fluid-structure interaction and the natural frequencies were obtained respectively. The results showed that the natural frequencies with consideration of fluid-structure interaction were smaller than that without this consideration.

top-suspended centrifuge; vibration characteristics; fluid-structure interaction; drum; analytical dynamic model; finite element method

广西制造系统与先进制造技术重点实验室主任基金项目(编号：13-051-09S08)；广西高校科研基金项目资助(编号：YB2014011)；广西高校临海机械装备设计制造及控制重点实验室培育基地开放课题基金资助(编号：GXLH2014KF-02)

杨旭娟(1983—)，女，广西大学副教授，博士。 E-mail: yxj413@163.com

2016—06—04

10.13652/j.issn.1003-5788.2017.01.016