双定子杯形转子感应电机磁路计算

姚江帆，欧阳斌，翟小飞

（海军工程大学舰船综合电力技术国防科技重点实验室，武汉 430033）

双定子杯形转子感应电机磁路计算

姚江帆，欧阳斌，翟小飞

（海军工程大学舰船综合电力技术国防科技重点实验室，武汉 430033）

为分析双定子杯形转子电机性能，分别采用传统磁路计算法和分布磁路法对其进行磁路计算，研究内定子和外定子各部分的磁通密度和磁压降。迭代计算给定相电压或励磁电流下的空载特性和激磁电感并与实验进行对比，结果与实测值相吻合，证明了分布磁路法的准确性和普适性。

双定子 感应电机 磁路计算 分布磁路法 空载特性

0 引言

双定子杯形转子感应电机是一种特殊结构的多相电机，其结构如图1所示，其内外两套独立定子绕组以及空心杯形薄壁转子的结构使其具有转动惯量低、响应速度快、转矩密度大、转矩波动小等优点[1]。小型双定子杯形转子电机在多个领域都有应用，文献[2]介绍了一种应用于机器人直驱的高扭矩电机，文献[3]详细设计了一种应用于能量回收领域的小型双定子杯形转子电机，文献[4]介绍了杯形测速发电机的计算。这些电机虽然在外观上类似本文所研究电机的缩小版，但它们的内定子均未开槽，没有嵌放绕组，所以从本质上看仍是三相感应电机，与本文电机在具体结构、功率/转矩密度上都有较大差异，因而表现出不同的性能。

为研究该双定子杯形转子电机的性能，首先应进行电机的磁路计算。现有的主磁路计算方法主要有：解析磁路法，磁网格法和有限元法[5]。传统的解析磁路法把电机分成每段包含一对极的若干扇形段，其中每一个扇形段的磁场简化为闭合磁回路，根据全电流定律，通过计算磁回路的磁场强度得到励磁磁势，再分别计算气隙磁密、定子齿部磁密和轭部磁密，经过饱和系数迭代最后得到电机的空载曲线。传统磁路法依赖极弧系数、气隙磁场波形系数和轭部磁压降矫正系数等需要查表的近似处理方式，这种方法针对正弦供电的电机虽然能快速求出最大磁密，但对于越来越普遍的多相电机适用性不强。近年来，有限元法发展迅速，得到广泛应用，但由于其计算周期长，灵活度较低，不适合电机前期设计和后期优化。分布磁路法[6]可以有效解决上述问题，这种方法一方面对磁路进行了网格剖分，不使用过多修正系数，能较细致地刻画出电机气隙磁场波形，在适用性和灵活性上优于传统磁路法；另一方面它通过MATLAB编程即可实现，计算快速方便，优于有限元法。

图1 双定子杯形转子电机结构示意图

本文分别用传统的解析磁路法和分布磁路法对双定子电机进行磁路计算，求出电机空载特性曲线和激磁电感参数并与实验结果作对比，验证了新方法在双定子杯形转子电机磁路计算中的准确性和有效性。

2 传统磁路法简要回顾

根据电机设计中介绍的传统磁路法[7]，构建双定子杯形转子电机磁路模型，以外定子为例，设 1～2段为气隙段，2～3段为外定子齿段，3～4段为外定子轭段，内定子方法一致，如图2所示。不同于传统三相异步电机，本文研究的双定子电机转子是薄壁光滑、没有绕组的，因此转子不是空载磁路的一部分。内定子和外定子绕组共同建立的旋转磁场作用于转子，使其感应出电磁转矩。

根据全电流定律，沿磁力线取正向积分，有

式中H为磁场强度，l为磁路积分路径，右边表示对应每极的励磁磁势。

由图2中对闭合磁回路的分段，式（1）变为

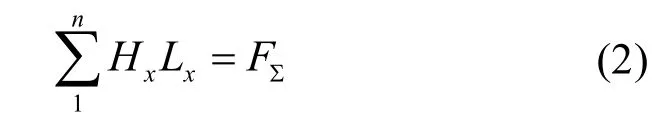
将励磁磁势的计算转化为磁路各段磁压降的计算。其中，气隙磁压降为

式中，δ为气隙径向长度， Kδ为计及齿槽效应引入的Carter系数，气隙磁密最大值Bδ由每极磁通Φ、计算极弧系数α’p、电机极距τ和磁路轴向有效长度lef确定，如下式：

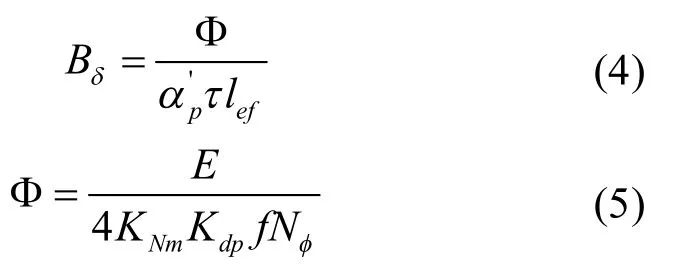
式中，E为相电势，KNm为气隙磁场波形系数，气隙磁场呈理想正弦分布时KNm等于1.11，为2/π，电机齿部越饱和，越大。Kdp为绕组系数，f为电流频率，Nφ为相绕组串联匝数。KNm和α通过预取的饱和系数Ks查曲线KNm= f(Ks)和= f(Ks)得到。

图2 双定子电机传统磁路模型

根据磁通连续原理，以内定子为例，齿部磁密Bti、轭部磁密Bji分别为

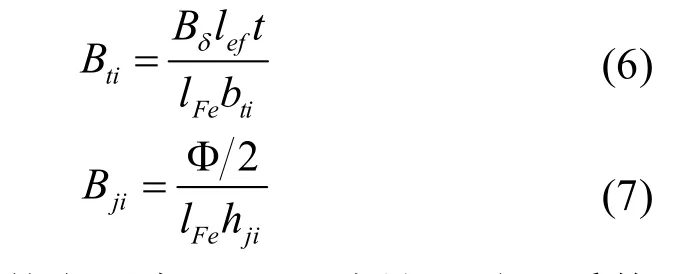
式中，t为内、外定子齿距，lFe为计及叠压系数的定子铁心轴向长度，bti近似为离齿最狭1/3齿高处的内定子齿宽，hji为轭高。

当齿磁密超过1.8T时，进行如下修正：其中，bs为槽宽，Hti是查 1.8T以上磁化材料曲线的磁场强度。

计算出准确的齿部磁密后查表获取磁场强度即可算出齿部磁压降。再将其代入饱和系数定义式

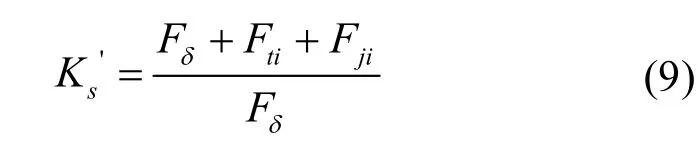
计算轭部磁压降时，应注意轭部磁压降校正系数Cji的引用

式中，Cji与轭尺寸、极对数和 Bji有关，Lji为每极齿联轭磁路计算长度。

得到各段磁压降后，可以求出闭合回路的磁压降和各电压下产生最大磁密的励磁电流需求，如下式

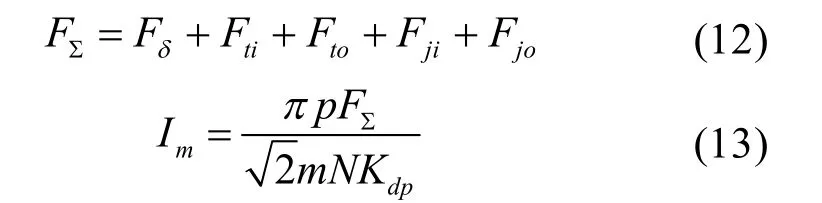
式中，Im为励磁电流，m为相数，p为极对数。

传统磁路法的核心是把气隙段、齿部、轭部分别等效为整体考虑，计算其各自的最大磁密。虽然程序编写较简单，迭代收敛也比较迅速，但在实际情况中，齿部和轭部的磁势、磁密都不是均匀的，因此引入下面的分布磁路法。

3 分布磁路法计算过程

分布磁路法是基于多个磁回路进行迭代处理的数值计算方法，依据磁势满足线性叠加关系，对定子进行等间隔周向分块，通过气隙磁密迭代计算出圆周气隙中心线上各节点的磁密、磁势及合成磁势，进而计算出激磁电感等。此计算方法所做的假设有：齿部磁力线为径向、轭部磁力线为周向、引入Carter系数计及内外定子齿槽效应等，与传统磁路法的假设一致。

3.1 磁路模型建立与划分

在双定子杯形转子电机半个极距范围内沿周向等间隔分块，对应电角度从 0到 π/2，沿径向进行磁路计算分区：气隙区（Ⅰ）、内定子齿部区（Ⅱ）、内定子轭部区（Ⅲ）、外定子齿部区（Ⅳ）、外定子轭部区（Ⅴ）。在磁路模型中，沿周向等角度均匀分为N块，对应气隙中心线上N+1个等间隔节点，如图3所示。

图3 磁路模型径向分区、周向分块

3.2 阶梯波磁势表达

双定子杯形转子电机的励磁磁势为阶梯波形式，在半个极距下，对 N+1个等间隔节点，设N1为内定子、外定子齿部区域包含的节点数，N2为槽部区域包含的节点数。

设Im0为空载励磁电流，q为每极每相线圈数，Nc为线圈匝数，q2为半个极距内包含的内/外定子齿数，k为计数值，取值范围从1～q2，interp1为MATLAB线性插值函数。根据绕组布置，有半个极距下的励磁磁动势F(i)表达如下：

i=1～3N1/2+N2，即对应第一个半个齿部、第一个槽部和第二个齿部时，

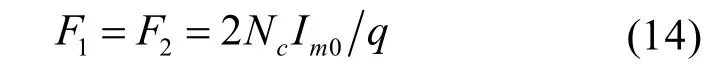
i=3N1/2+N2+1～3N1/2+2N2，即对应第二个槽部时，

i=3N1/2+2N2+1～5N1/2+2N2，即对应第三个齿部

时，

以此类推，在对应第(k+1)个齿部，即

i=(2k-1)N1/2+kN2+1～(2k+1)N1/2+kN2时，

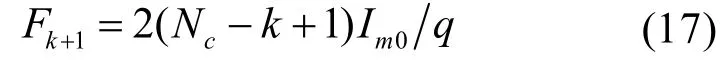
i=(2k+1)N1/2+kN2+1～(2k+1)N1/2+(k+1)N2时，

特别地，对应第(q2-1)个齿部时，

在第(q2+1)个齿部，即最后半个齿部区域节点上，i=(2q2-1)N1/2+q2N2+1～N+1时，有= 0 。

3.3 各段回路磁密和磁压降计算

给定励磁电流Im0一个初值，同时预设一个饱和系数值kst，第i节点处气隙磁密Bδ(i)为

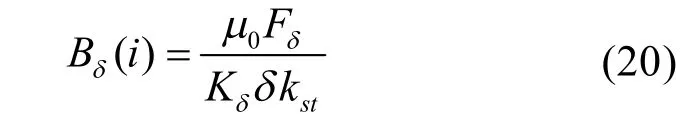
在齿不太饱和时，认为磁场全由齿中通过。即i=(2k-1)N1/2+kN2+1～(2k+1)N1/2+kN2时，第i节点处内定子、外定子齿部磁密Bti(i)和Bto(i)为

式中，Bδav为齿部对应节点气隙磁密的平均值，bti和 bto分别为内定子、外定子齿宽。其余节点的齿部磁密为0。

当齿磁密大于1.8T时，认为因磁路饱和磁通并未全部从齿中通过，有少部分流进槽中，故引入类似传统磁路法中的修正关系：

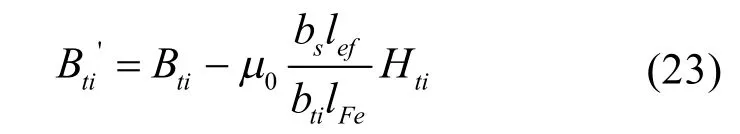
对于轭部磁密，同样根据磁通连续性原理，第1节点与第i节点间气隙中心面上的径向磁通等于第i节点处轭部截面上的周向磁通，因此第i节点处内定子、外定子轭部磁密Bji(i)和Bjo(i)分别为

式中，hji、hjo分别为内定子轭高和外定子轭高。

根据第i节点处内定子、外定子齿部和轭部磁密，查材料磁化曲线得到对应的磁场强度Hti(i)、Hji(i)和 Hto(i)、Hjo(i)。因此闭合磁回路各段的磁压降分别为

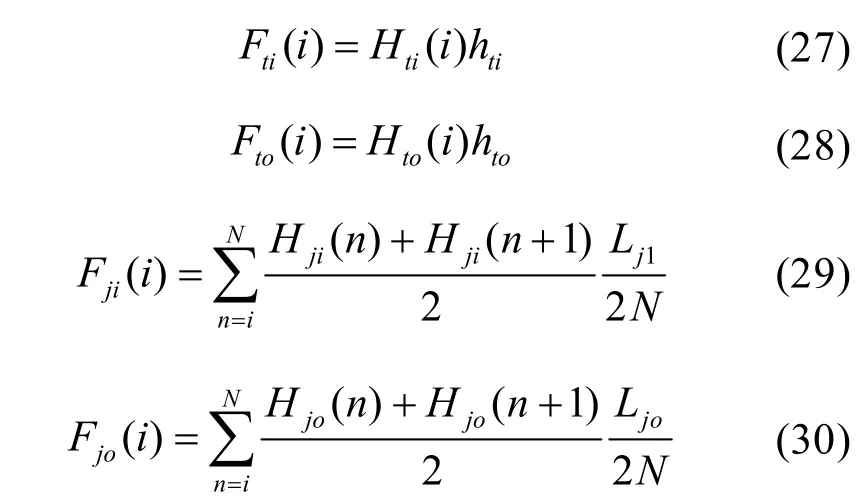
式中，hti、hto分别为内定子、外定子齿高，Lj1、Lj2分别为内定子、定子每极齿联轭磁路计算长度。

经过第i节点的闭合回路总磁压降为

3.4 气隙磁密迭代

由安培环路定律，闭合磁路中的总磁压降等于磁势。对1～N范围内的每一个节点对应的闭合磁路，磁压降应等于该节点的励磁磁势。对两个磁势向量，认为它们之间的相对距离d小于给定精度ε就表示磁势相等，即

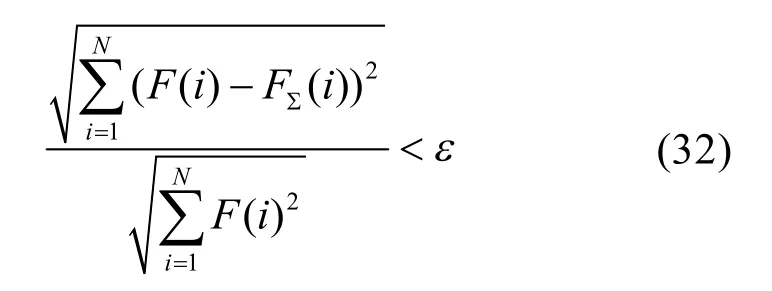
若式(32)不满足给定精度，则对气隙磁密Bδ(i)进行如下修正，代回计算程序重新计算，直到满足精度。第i节点处的修正气隙磁密B´δ(i)为

式中，kB为修正系数，取值范围为 0.05～0.5，一般饱和程度较低时取大值，饱和程度高时取小值，取大值可能发散，取小值迭代次数增多。

根据磁势的奇偶对称性将气隙磁密值由半个极距延拓至一对极范围，即从1/4个周期延拓到1个周期。用MATLAB中傅里叶函数分解得到气隙磁密基波幅值，以及各次谐波分布。

4 计算结果与实验结果比较验证

4.1 气隙磁密分布分析

根据前述两种双定子杯形转子电机磁路计算方法，利用MATLAB软件编写计算程序，分别用两种方法计算电机的气隙磁密分布。其中，分布磁路法计算值延拓后一个周期下的气隙磁密分布如图4所示。

可以看出，分布磁路法计算出的气隙磁密分布体现了阶梯波磁势的特征。而传统磁路法利用计算极弧系数和极弧计算长度描绘气隙磁密分布，只能粗略地描述气隙磁密变化趋势同计算极弧系数的关系（齿部越饱和，气隙磁场波形越平，计算极弧系数越大），不能像分布磁路法这样从阶梯波磁势的角度表现更贴近真实的磁密变化。这一点说明分布磁路法相对传统磁路法计算结果更加丰富，便于后续作其他分析。

4.2 空载特性比较验证

空载实验由外部三相电源拖动双定子杯形转子电机加速到空载转速，在空载运行稳定后，通过Synergy采集电机转速、内定子和外定子三相电流、两相线电压数据以及电机输入功率。取95Hz这一工作点进行数据分析，将得到的空载特性曲线同计算结果进行对比。由于空载磁路计算时忽略端部漏电感和槽部漏电感，而实验所测得的端部电压包含这两项，因此将计算值计及定子总漏感的影响，得到传统方法与分布磁路法计算结果与实验结果对比如图5所示。

由图5可知，分布磁路法和传统磁路法的理论计算值与实验结果总体误差在 4%以内，两种方法计算结果相差不大，说明利用这两种方法对双定子杯形转子电机进行磁路计算较为准确，电机空载特性与预期结果也相差不大。

进一步分析，可知当饱和程度较低时，计算值与实测值吻合度较高；随着气隙磁密饱和加深，传统磁路法计算得到的相同电压下的励磁电流需求较实测偏小。这一现象是磁路模型简化考虑、引入修正系数进行等效共同造成的，用分布磁路法也产生同样的结果，其主要原因在于Carter系数计及定子齿槽效应[8]。卡特系数是在不考虑饱和并假设槽型为无限深矩形槽的理想情况下利用许克变换所得的解析式，所以在饱和以及槽深有限的情况下，实际等效气隙长度并不等于计算方法中用卡特系数计算出的等效气隙长度。

由于分布磁路法中磁路模型按网格划分，磁场描述更加细致，减少了对参数查表的依赖，所以该方法较传统方法更加灵活，通用性和一般性较好。

图5 两种方法计算值与实验空载特性对比

4.3 激磁电感求取与对比

由空载磁路计算得到气隙基波磁密分布和最大值后，可由式(34)和式(35)分别算出每极基波磁通最大值Φ1m和感应电势基波有效值E1。

式中，Bδ1m为气隙基波磁密最大值，Kdp1为基波绕组系数。

在给定基波相电压有效值计算磁路的情况下，可由空载等值电路推导出激磁电抗，由式(36)给出。双定子杯形转子感应电机理想空载运行时转差率为 0，忽略激磁电阻和定子电阻，其空载等值电路为激磁电抗和定子漏抗串联的一条支路。

式中，Im1为基波激磁电流有效值，U1为相电压有效值，Xm1为激磁电抗，Xl为定子漏抗。

进而由式(37)计算出激磁电感参数，即

表 1给出此电机在额定工况下传统磁路法（方法1）和分布式磁路法（方法2）对激磁电感的计算结果与实测值及相对误差。可以看出，两种方法计算出的激磁电感参数相差不大，与实测值相对误差也较小。

表1 激磁电感计算值与实测值比较

5 结语

本文分别用传统磁路法和分布磁路法对双定子杯形转子电机展开了磁路计算，得出该电机各部分的磁密分布和空载特性曲线，并据此计算出激磁电感参数，将理论计算值与实验值进行了对比，结果均较为准确。比较分析两种方法，分布磁路法普遍适用性更强且计算结果更加丰富，在计算双定子杯形转子电机的磁路中具有推广意义。

[1] 柴凤, 崔淑梅, 程树康, 双定子电机发展状况及展望[J]. 微特电机, 2001, 05: 23-26.

[2] Ross Welburn, Lira L. Ultra high torque motor System for direct drive robotics[C]. Robots 8 Conference Proceeding Applications, Detroit, Michigan, 1984: 1963-1971.

[3] Mladen V. Terzic, Dragan S. Mihic, Slobodan N. Vukosavić. Design of high-speed, low-inertia induction machines with drag-cup rotor[J]. IEEE Transactions on Energy Conversion, 2014, 29(1) : 169-177.

[4] 黄璞, 王双寿, 严关森, 空心杯转子异步测速发电机的计算[J]. 微特电机, 1976, 04: 51-62.

[5] 管少华, 程思为, 王东, 等. 用于感应电机设计的分布磁路法快速迭代方法[J]. 电机与控制应用, 2016, 43(6): 17-22.

[6] WANG D, WU XZ, CHEN JQ, et al. A distributed magnetic circuit approach to analysis of multiphase induction machines with non-sinusoidal supply[J]. IEEE Transactions on Energy Conversion, 2015, 30(2): 522-532.

[7] 陈世坤. 电机设计[M]. 北京: 机械工业出版社, 2002: 23-42.

[8] 王东, 吴新振, 马伟明, 等. 非正弦供电十五相感应电机磁路计算方法[J]. 中国电机工程学报, 2009, 29(12): 58-64.

Magnetic Circuit Calculation of Dual-stator Induction Machine with Drag-cup Rotor

Yao Jiangfan, Ouyang Bin, Zhai Xiaofei
(National Key Laboratory of Science and Technology on Vessel Integrated Power System, Naval University of Engineering，Wuhan 430033, China)

In order to analyze the performance of dual-stator induction machine, magnetic calculation is made by conventional magnetic approach and distributed magnetic circuit approach(DMCA) respectively. Magnetic flux density and magnetic potential drop in each sections of inner stator and outer stator are studied. No-load characteristic and magnetizing inductance are calculated by iterative method under given phase voltages or exciting currents and compared with experiments. The agreement between calculated results and measured ones demonstrates the accuracy and universality of DMCA.

dual-stator；induction machine；magnetic calculation；distributed magnetic circuit approach；no-load characteristic

TM346

A

1003-4862（2017）02-0048-06

2016-10-12

国家自然科学基金资助项目（51407190）。

姚江帆(1992-)，男，硕士研究生。研究方向：集成化发电技术。E-mail:cnjfyao@163.com

欧阳斌(1981-)，男，博士，副教授。研究方向：电机设计分析及控制技术。