一种基于PSO整周模糊度逆向求解的GNSS测姿算法

戴 卿，常允艳,2

(1.重庆水利电力职业技术学院 建筑工程系，重庆 402100；2.中南大学 地球科学与信息物理学院，湖南 长沙 410083)

随着 GNSS（Global Navigation Satellite System）载波相位技术的快速发展，导航与位置服务科学在测绘、交通、航空、安防等诸多领域取得了广泛的应用。GNSS天线不仅能给用户提供准确的时间和位置信息，还能完成高精度的载体实时姿态测量任务。而载波相位测量的整周模糊度求解问题作为GNSS实时测姿的核心，一直是国内外众多学者的关注热点[1-2]。近几年来先后涌现出大量关于模糊度求解的技术和方法，主要归为四类。基于测量域的整周模糊度求解，操作简单，观测时间短，实时性好，但仅适用于短基线测量。基于观测域的整周模糊度求解，利用卫星伪距测量值确定模糊度，但测量值精度会直接影响求得模糊度精度。以模糊度函数法为代表的基于位置域的整周模糊度求解作为发展较为完善的方式，对初值的依赖较大，且易出现由于估计精度差而导致无解或搜索次数剧增的情况。基于模糊度空间的整周模糊度搜索，主要借鉴最小二乘算法和滤波技术，比较有代表意义的有最小二乘搜索、快速求解模糊度法和LAMBDA算法 (Least Squares Ambiguity Decorrelation Adjustment)等，但这些算法属遍历方法，搜索效率较低，实时性欠佳[3-5]。

粒子群优化算法 （Particle Swarm Optimization,PSO）受群体运动行为的研究产生，通过个体间的协作在求解全局优化中具有自适应和自学习特点，易实现，计算效率高。因此，本文将其用于改进传统模糊度搜索，不仅可免去整周模糊度去相关处理等过程，可实现性好，而且在搜索效率上有较大提高。最后根据所得高精度的载波相位观测值用于求解基线矢量，实现载体的实时姿态确定。通过实测数据表明，新算法相比基于GA模糊度搜索方式成功固定率明显提高，测姿精度好，收敛速度快，可为GNSS动态测姿工程应用提供借鉴价值。

1 基线初始姿态角搜索

如文献[5]所述，组成不大于3 m的基线矢量b，然后通过解算b的姿态角确定载体姿态。则天线A和天线B对同一时刻观测的两颗卫星i和j的载波相位双差为

式中b表示基线长度，λ表示载波波长，α和β分别表示基线矢量的航向角和俯仰角，αi和αj分别表示基线对载波平面的高度角，Ωi和Ωj为卫星i和卫星j对基线的载波平面的方位角，Nij为双差模糊度参数，δij为均值为0的高斯白噪声序列。

因双差方程可消除钟差、电离层误差和对流层误差等各种误差源，因此（1）式的数学期望是整数：

上式的目标函数值为1，即

式中基线的航向角φ和俯仰角β为不确定参数，可通过非线性组合优化思路求解载体姿态问题。通过观测n颗卫星和m个历元构成的约束条件，建立适应度函数，搜索唯一解。

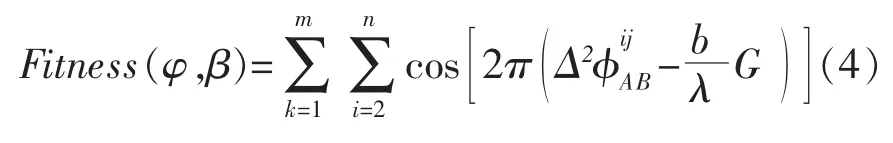
2 逆向求解整周模糊度

2.1 根据姿态角求基线矢量

确定载体基线航向角φ、俯仰角β和基线长度b后，进行坐标转换求解基线在当地水平笛卡尔儿坐标系下的三维分量［XzsYzsZzs］

转换为地心坐标系,

其中Lp、Bp表示观测点经纬度坐标，基线矢量为b=［ΔX ΔY ΔZ］。

2.2 求双差整周模糊度

由相位双差观测方程简洁表达式

其中Φ表示相位双差值矩阵，N表示双差整周模糊度矩阵，b表示基线矢量，e表示观测噪声误差矢量 （均值为0，方差为Q）,A和B分别表示N和b的设计矩阵。

对上式进行最小二乘估计，得到实数估计值Nˆ、bˆ和协方差矩阵为若已知基线矢量b，则可逆向求双差整周模糊度，即

最后实时解算基线姿态

3 PSO算法描述

粒子群优化算法 （Particle Swarm Optimization,PSO）是一种群体智能算法,由Eberhart博士和kennedy博士发明[7]。作为一种群体智能优化算法，PSO算法简洁易于编程实现，可调参数少，无梯度信息，因此在非线性优化、组合优化等领域有很大优势。算法中，将组合优化问题的潜在解用d维搜索空间上的粒子来表示，这些粒子以特定的速度飞行并进行动态调整，最终最优值的确定通过目标函数适应值来确定，将其用于改进模糊度搜索可提高搜索效率，改善模糊度固定解的成功率。PSO算法搜索过程如图1所示，相关具体计算步骤见文献[7]。

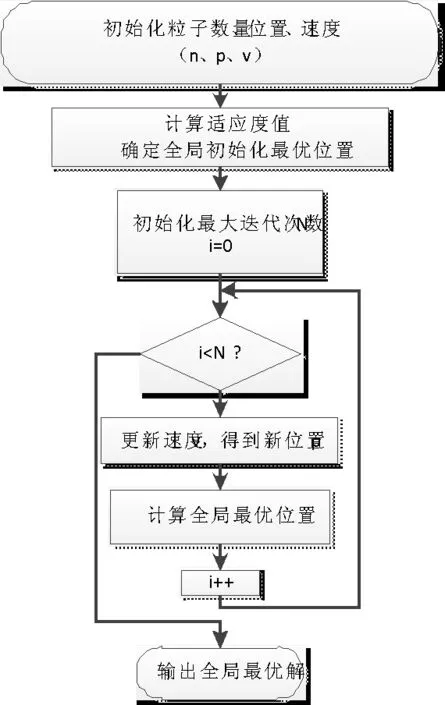
图1 PSO算法搜索过程Figure 1 PSO algorithm search process

由此可见，通过式（4）PSO算法高效的搜索策略获取GNSS基线的初始姿态角，并由式（9）求出双差模糊度N，最后基于式（10）对基线姿态角实时解算。这种免去整周模糊度直接搜索的方法，较易编程实现，且在动态解算中具有较好的稳定性。

4 实测数据验证与分析

为验证本文所提算法在GNSS测姿数据处理中的效果，实验使用两GPS-701-GG天线，接收板模块为OEMV-1G，可输出频率为20 Hz的天线位置、卫星坐标和L1载波等数据，并由RS-232串口连接计算机，基于matlab开发算法测试平台，进行实时解算。（计算平台：i5-4210U,RAM4G,Win10,Matlab2014a）

4.1 GNSS静态测姿实验

设置基线长度为1m的静态测姿实验，利用精确指北针和高精度机械陀螺仪测定值作为参考值，进行GNSS静态测姿实验，结果如表1所示。

表1 静态测姿实验结果Table 1 Results of static test position

实验数据表明：GNSS静态测姿中航偏角输出误差优于0.03°，俯仰角输出误差优于0.04°，且误差方差值偏小，均保证在0.015以内。整体来说基于PSO模糊度搜索的测姿算法在GNSS静态测姿性能方面表现较为稳定，姿态解算精度较高，

4.2 GNSS动态测姿实验

为进一步验证新算法在GNSS实时动态测姿中的性能，设置不同动态条件下（基线转速为 5 s/转，15 s/转和24 s/转）的PSO算法测姿实验，测试中将基于遗传算法（Genetic Algorithm,GA）的搜索方法作为对比项进行性能讨论。

图2 基于PSO算法模糊度搜索的测姿结果Figure 2 The results of themeasurementof fuzzy degree search based on PSO algorithm

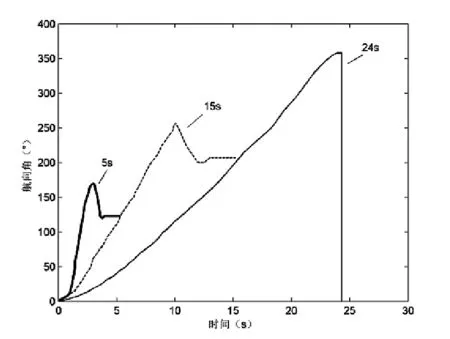
图3 基于GA算法模糊度搜索的测姿结果Figure 3 The results of the detection of fuzzy search based on GA algorithm

表2 动态测姿实验结果Table 2 Experimental results of dynamicmeasurement

如图2和图3对比了不同算法下模糊度搜索影响的测姿结果，由结果可见：

1）基于GA模糊度搜索的测姿算法相比本文所提新算法在5 s/转和15 s/转时，由于模糊度搜索未能准确得到固定解，导致姿态解算中出现问题。分析原因可能是由于GA算法不能确保对全局最优解的搜索，当载体运动时搜索可能陷入局部最优值，降低模糊度搜索成功率，从而影响动态测姿性能。

2）在表2中对比发现，基于PSO模糊度搜索的测姿算法比基于GA模糊度搜索的测姿算法在模糊度固定解的搜索成功率方面高出17%，且迭代次数较少，计算效率提高了约21%。

由此可见，提出的基于PSO的模糊度搜索方法在三种不同动态状态下，输出结果较为稳定，较适合动态测姿数据处理，更为适合将来的工程使用。

5 结论

载波相位整周模糊度的准确和高效解算，是实现GNSS实时动态测姿的关键问题。本文在传统模糊度求解的基础上，考虑粒子群优化算法在解决复杂组合优化问题上的优点，讨论算法的鲁棒性和收敛速度，避免传统生物进化算法在搜索整周模糊度固定解遇到的收敛速度慢和易陷入局部最优解的问题。最后通过实测数据，表明新算法用于GNSS静态测姿实验，输出精度较高，结果稳定可靠；用于GNSS动态测姿实验，相比基于GA模糊度搜索的测姿算法，计算结果精度好，模糊度成功固定率显著提高，收敛速度较快，在计算精度和计算时间上都有所提升。

[1]GROVES P.Principles of GNSS,Inertial,and Multisensor Integrated Navigation Systems[M].Boston/London:Artech House,2015:58-76.

[2]傅英定,成孝予,唐应辉.最优化理论与方法[M].北京:国防工业出版社出版2007:120-247.

[3]何正斌.GPS/INS组合导航数据处理算法拓展研究[D].西安：长安大学，2012:25-45.

[4]吴铁军，马龙华，李宗涛.应用捷联惯导系统分析[M].北京：国防工业出版社，2011:15-78.

[5]GIORGIG.GNSSCarrier Phase-based Attitude Determination Estimation and Applications [D].Delft University of Technology,2011:5-24.

[6]KIM Y,SONG J,PARK B,etal.GPSCycle-slip Detection with Low-cost IMU and Single-frequency Receiver of Land Vehicle[C].Proceedingsof the IONPacific PNT,Hawaii,2013:1032-1040.

[7]刘衍民.粒子群优化算法的研究及应用[D].济南:山东师范大学,2011:19-20.

[8]KOTHARIR,GHOSH D.An Efficient Genetic Algorithm for Single Row Facility Layout[J].Optimization Letters,2014,8(2):679-690.

[9]刘朝华.混合免疫智能算法理论及应用[M].北京:电子工业出版社,2014:1-30.