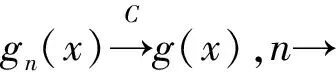END序列下非参数回归模型估计的相合性与完全收敛性

邢韵

(湖北大学数学与统计学学院,湖北 武汉 430062)

END序列下非参数回归模型估计的相合性与完全收敛性

邢韵

(湖北大学数学与统计学学院,湖北 武汉 430062)

研究误差为END序列的非参数回归模型未知函数估计量的极限性质.并利用END序列的Cr不等式,Rosenthal不等式以及权函数相关性质, 证明其弱相合性与完全收敛性.

非参数回归模型;END序列;相合性;完全收敛性

0 引言

设p是一个正整数,A是Rp上的紧集,考虑下面的非参数回归模型:

Yni=g(xni)+εni,i=1,2,…,n

(1)

其中g(·)是定义在紧集A上的未知函数,xi∈A(i=1,2,…,n)为已知的固定设计点列, {εni,1≤i≤n,n≥1}为END变量序列.假定对每个n,{εn1,εn2,…,εnn} 与{ε1,ε2,…,εn}为 同分布的.定义g(x)的加权回归函数估计为:

(2)

其中Wni(x)=Wni(x,x1,x2,…,xn)为仅依赖于固定设计点列的可测的加权函数.

上述的估计最初是由Georgiev提出来的,之后就有许多学者对其进行相关的研究.Georgiev等[1]研究了在独立情形下gn(x)的相合性与渐近正态性,Fan[2]和Hu等[3]研究了Lp混合情形下gn(x)的相合性、正态性和平均相合性,Liang等[4]讨论了误差为NA情形下gn(x)的相合性,刘婷婷等[5]研究了误差为AANA时的gn(x)的p阶平均相合性和一致p阶平均相合性. 本文中研究随机误差为END情形下gn(x)的相合性与完全收敛性.

设{Xn,n≥1}是随机变量序列,X为一非负随机变量,C>0为常数, 若对任意的x>0,n≥1, 都有P(|Xn|>x)≤CP(X>x),则称{Xn,n≥1}是被X随机控制的.本文中约定:an=O(bn)表示anCbn,其中C表示与n无关的正常数,并且在不同的地方可以表示不同的值,IA表示示性函数,C(g)表示gn(x)在A上的连续点. 另外,||x||记为点x在Rp中的欧氏模,g(·)在紧集A上连续.

在非参数回归模型(1)中,对任意固定的x∈A,有关权函数Wni(x)=Wni(x,xn1,xn2,…,xnn)的假设如下:

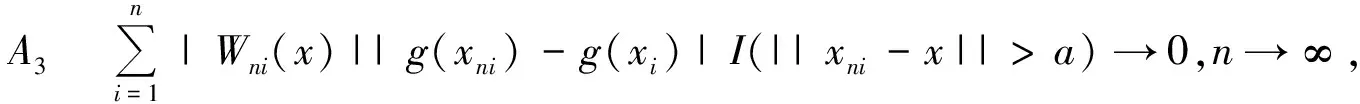
1 相关定义与引理

定义1[6]设(Ω,F,P)为概率空间,{Xn,n≥1}为随机变量序列, 称随机变量X1,X2,…,Xn是END(extended negatively dependent)的,如果存在正常数M,使得对任意实数x1,x2,…,xn同时成立

和

称随机变量序列{Xn,n≥1}是END的,如果任意有限个随机变量是END的.称随机变量阵列 {Xni,i≥1,n≥1}是END的,如果对任意的n≥1,随机变量序列{Xni,i≥1}是END的.

引理1[6]?偅j设X1,X2,…,Xn是END随机变量,f1,f2,…,fn全部是非降或非增函数,则f1(X1),f2(X2),…,fn(Xn)也是END随机变量.

引理2[7](Rosenthal不等式) 设{Xn,n≥1}是一均值为零的END随机变量序列, 且对p≥2和所有n≥1有E|Xn|p<∞,则

其中Cp为只依赖于p的正数.

引理3[8]对任意的q>0,a>0,有

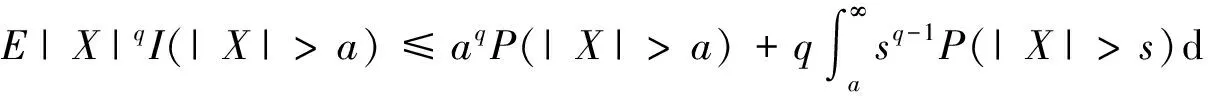
引理4[8]对任意的r>0,有

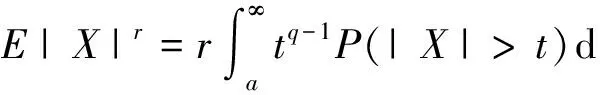
2 主要结论

定理1 设模型(1)中的g(x)的估计是由(2)式所定义的,随机误差{εni,1≤i≤n}是END序列, 且被X随机控制,对r>1,条件A1,A2,A3满足并且

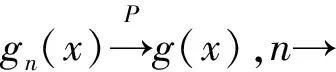
定理1的证明 对于x∈C(g)和a>0,由(1)式和(2)式有

由假设条件A1,A2,A3和g(·)在紧集上连续,我们有

|Egn(x)-g(x)|→0,x∈C(g),n→∞

(3)

接下来我们证明

记

Xni=εniI(|εni|≤n)+nI(εni>n)-nI(εni<-n),

所以

而

(4)

又由引理3可以知道

(5)

于是要证明J→0,只要证明

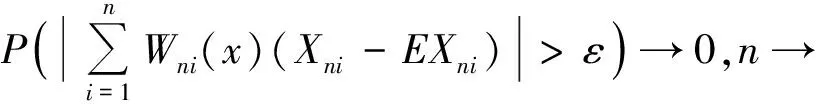
由引理1可知{Wni(x)(Xni-EXni),1≤i≤n}仍是END序列.由引理2和Cr不等式可知

易见

(6)

由引理3可得

(7)

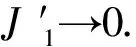
(8)

最后证明J″1→0.当1

(9)

当r≥2时,

(10)

定理2 假设{εni,1≤i≤n}为END变量序列,且被X随机控制, 并且假设条件满足A1,A2,A3.如果对01/p使得

定理2的证明 对于x∈C(g)和a>0, 由(1)式和(2)式有

(11)

由于x∈C(g),因此对∀ε>0,∃δ>0,使得当||xni-x||<δ时,有||gni-g(x)||<ε. 因此,假定(11)式中的0

根据(3)式,我们只需要证明

因此我们只需证明对∀x∈C(g),有Ii<∞,其中i=1,2,3,4.

由0

由引理2,当q≥2时我们有

我们先证明I1→0,由Cr不等式和条件A2可得

(12)

再证明I12,因为0

(13)

由(12)、(13)式及文献[9]中的定理2知I1<∞.

(14)

我们取充分大的N,使得-((2αp-1)-2pρ)N<-1,那么I2<∞.

最后来证明I4<∞.当E|X|2p<∞和α>1/p>0时,我们有

(15)

[1] Georgiev A A, Greblicki W. Nonparametric function recovering from noisy observations[J].Journal of Statistical Planning and Inference, 1986, 13(1): 1-4.

[2] Fan Y. Consistent nonparametric multiple regression for dependent heterogeneous processes: the fixed design case[J].Journal of Multivariate Analysis, 1990, 33(1): 72-88.

[3] Hu S H, Zhu C H, Chen Y B,et al. Fixed-design regression for linear time series[J].Acta Mathematica Scientia,2002,22(1): 9-18. [4] Liang H Y, Jing B Y. Asymptotic properties for estimates of nonparametric regression models based on negatively associated sequences[J].Journal of Multivariate Analysis, 2005, 95(2): 227-245.

[5] 刘婷婷,陈志勇,魏芸菲，等. 误差为AANA序列时非参数回归模型估计的相合性[J].合肥学院学报, 2013, 23(1): 17-19.

[6] Liu L. Necessary and sufficient conditions for moderate deviations dependent random variables with heavy tails[J].Science in China Series A:Mathematics, 2010, 53(6): 1421-1434.

[7] Shen A. Probability inequalities for END sequence and their applications[J].Journal of the Inequalities and Application, 2011, 98: 1-12.

[8] Gail S X, Chen P Y. Some limit theorems for weighted sums of arrays of NOD random variables[J].Acta Mathematica Scientia, 2012, 32B(6): 2388-2400.

[9] 邢韵. END序列下半参数回归模型估计的相合性[J].湖北大学学报(自然科学版)，2017,39(2)：118-122,130.

(责任编辑 赵燕)

The consistency and complete convergence of estimators in non-parametric regression model with END sequences

XING Yun

(Faculty of Mathematics and Statistics, Hubei University, Wuhan 430062,China)

In this paper, based on END errors, the limit properties for unknown functiong(·) in the nonparametric regression model is investigated.By usingCrinequality,Rosenthal inequality,and some properties of weighted functions, we obtained the weak convergence and complete convergence.

non-parametric regression model; END sequences; consistency; complete convergence

2016-07-03

邢韵(1993-)，女，硕士生

1000-2375(2017)02-0118-07

O212.2

A

10.3969/j.issn.1000-2375.2017.02.003