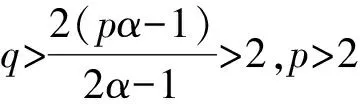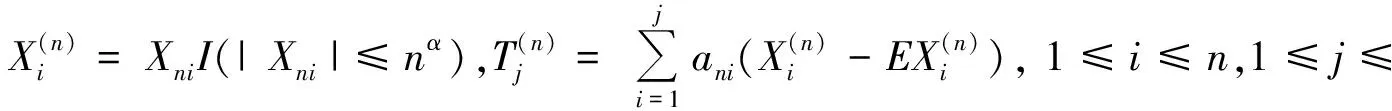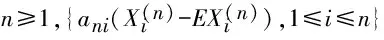(α,β)混合序列加权和的完全收敛性

余超群

(湖北大学数学与统计学学院,湖北 武汉 430062)

(α,β)混合序列加权和的完全收敛性

余超群

(湖北大学数学与统计学学院,湖北 武汉 430062)

借助(α,β)混合序列加权和的极大值矩不等式,采用截尾的方法讨论(α,β)混合序列加权和的完全收敛性,并获得(α,β)混合序列加权和的Marcinkiewicz-Zygmund型强大数定律.

(α,β)混合序列;Marcinkiewicz-Zygmund型强大数定律;完全收敛性;加权和

0 引言

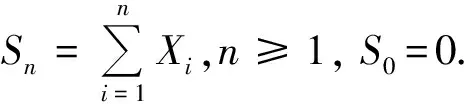
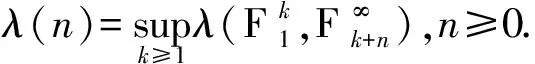
(α,β)混合序列的定义由Bradley[1]给出,并研究了绝对正则条件下(α,β)混合序列的中心极限定理.邵启满[2]进一步研究 (α,β)混合序列的极限性质.陆传荣等[3]于1997年建立了(α,β)混合序列协方差的界,在此基础上, 沈燕[4]给出了(α,β)混合序列的矩不等式,得到(α,β)混合序列的收敛定理.赵琦[5]利用Kolmogorov不等式得到(α,β)混合序列 的三级数定理,在较弱的条件下,进一步研究了(α,β)混合序列的部分和与乘积和的强大数定律和加权和的完全收敛性.在本文中,我们借助(α,β)混合序列加权和的极大值矩不等式,采用截尾的方法讨论(α,β)混合序列加权和的完全收敛性,并获得(α,β)混合序列加权和的Marcinkiewicz-Zygmund型强大数定律.

设{Xn,n≥1}是随机变量序列,X为一非负随机变量,C>0为常数, 若对任意的x>0,n≥1, 都有P(|Xn|>x)≤CP(X>x),则称{Xn,n≥1}是被X一致控制的.本文约定:C,C1,C2总表示正常数, 且在不同的地方可以表示不同的值.

1 引理

引理1[6]设{Xn,n≥1}是被随机变量X一致控制的序列,则对∀α,b>0有

E|Xn|αI(|Xn|≤b)≤C1[E|X|αI(|X|≤b)+bαP(|X|>b)]

(1)

E|Xn|αI(|Xn|>b)≤C2E|X|αI(|X|>b)

(2)

其中C1,C2都是正常数.

其中C为仅依赖于α,β和λ(·)的常数.

2 主要结果及证明

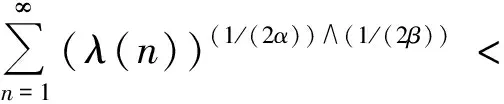
(3)

若存在一常数q>max{α,2(pα-1)/(2α-1)},使得E|X|q<∞,则对∀ε>0,有

(4)

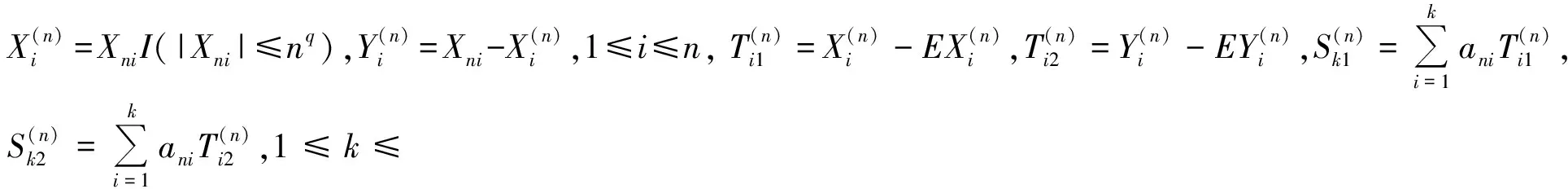
(5)

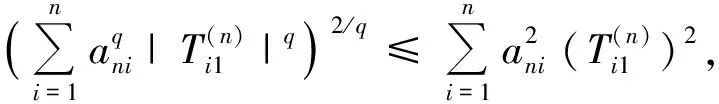
(6)

因为q>2(pα-1)/(2α-1),由Markov不等式和(6)式可得

(7)

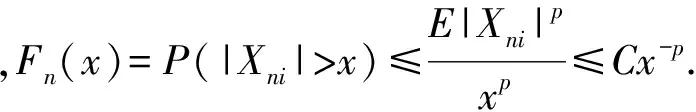
(8)

并由(3)式和Hölder不等式,对于1≤k

(9)

(10)

因此,结合(5)式,(7)式和(10)式有(4)式成立.定理证毕.

(11)

(12)

首先,我们将证明

(13)

当1/2<α≤1时,由E|X|q<∞,EXni=0,引理1(2)式,(11)式和(9)式(取k=1)可得

当α>1和p≥1时,由E|X|q<∞,(11)式和(9)式(取k=1和q=2)可得

当α>1和p<1时,由(11)式和(9)式(取k=1和q=2)可得

由条件pα≥1和E|X|p<∞可知

nP(|X|>nα)=nP(|X|p>npα)≤nP(|X|p>n)≤E|X|pI(|X|p>n)→0,n→∞

(14)

同时,由p<1和αp≥1可得

(15)

为了证明(4)式,只需要证明I<∞和J<∞.

(16)

因为α>0和0

(17)

因此,结合(15)～(17)式有(4)式成立.定理证毕.

(18)

和

(19)

推论1的证明 在定理2中取αp=1,立即可得(18)式成立.因此

根据Borel-Cantelli引理可得

(20)

对于任意正整数n,都存在一正整数i0满足2i0-1≤n<2i0.由(20)式可得

从而,(19)式成立.

(21)

其中0<δ≤min{1,α/2}.则对∀ε>0,有(4)式成立.

从而,有(12)式成立,由(21)式和Hölder不等式,则对1≤k<α,有

(22)

当α>1和p≥1时,由引理1,(22)式(取k=1)和(14)式可得

当α>1和p<1时,由引理1,(22)式(取k=1)和(14)式可得

因此,有(13)式成立. 进一步,由(12)式和(13)式可得

为了证明(4)式,只需要证明H<∞和G<∞.类似于(16)式的证明可得H<∞.因此,只需验证G<∞即可. 当α>2时,由Markov不等式,引理1,引理2,(22)式(取k=2)和0

(23)

当1<α≤2,由Jensen不等式可知,对于任意的1<α≤k,

(24)

推论2的证明 在定理3中取αp=1,立即可得(18)式成立.另一方面,类似于推论1的(19)式证明过程,同理可证(19)式成立.

定理4的证明 对固定的n≥1,记

从而,有(12)式成立. 因为0<α≤1,由EXni=0,引理1(2)式和(24)式(取k=1)可得

因此,有(13)式成立.进一步,由(12)式和(13)式可得

为了证明(4)式,只需要证明E<∞和F<∞.类似于(16)式的证明可得E<∞.因此,我们只需验证F<∞即可.因为0<α≤1,在(24)式(取k=2)可得

类似于(23)式的证明,我们可得到F<∞. 定理证毕.

推论3的证明 类似于推论2的证明过程.

[1] Bradley R C. On the central limit question under absolute regularity[J].Ann Probab, 1985(4): 1314-1325.

[2] Shao Q M. Almost sure invariance principles for mixing sequences of random variables[J].Stochastic Processes and Their Applications, 1993(2): 1-9.

[3] 陆传荣, 林正炎. 混合相依变量的极限理论[M].北京: 科学出版社, 1997.

[4] 沈燕, 张永军，王学军，等.(α,β)混合序列的强极限定理[J].中国科学技术大学学报, 2011(9): 778-784.

[5] 赵琦.(α,β)混合序列部分和与乘积和的强大数定律[J].湖北大学学报(自然科学版)，2015(3): 213-217.

[6] 吴群英.混合序列的概率极限理论[M].北京：科学出版社, 2006.

[7] 余超群.(α,β)混合序列加权和的强收敛性[J].湖北大学学报(自然科学版),(已录用待发表)

(责任编辑 赵燕)

Complete convergence theorems of weighted sum for (α,β) mixing sequences

YU Chaoqun

(Faculty of Mathematics and Statistics, Hubei University, Wuhan 430062,China)

We used the maximal inequality for weighted sums of (α,β) mixing sequence,and the truncated method to discuss the complete convergence theorems of weighted sum for (α,β) mixing sequence,and then got the Marcinkiewicz-Zygmund-type strong law of large numbers for weighted sums of (α,β) mixing sequence.

(α,β) mixing sequence;Marcinkiewicz-Zygmund-type strong law of large numbers;complete convergence theorems; weighted sum

2016-06-12

余超群(1991-)，女，硕士生

1000-2375(2017)02-0123-08

O211.4

A

10.3969/j.issn.1000-2375.2017.02.004