基于动态模糊阈值的电池组均衡策略优化

刘征宇 马亚东 孙 庆 汤 伟

1.合肥工业大学机械与汽车工程学院,合肥,2300092 安全关键工业测控技术教育部工程研究中心,合肥,230009

基于动态模糊阈值的电池组均衡策略优化

刘征宇1，2马亚东1孙 庆1汤 伟1

1.合肥工业大学机械与汽车工程学院,合肥,2300092 安全关键工业测控技术教育部工程研究中心,合肥,230009

简单地以固定的端电压阈值作为动力电池组均衡控制指标，可能会导致均衡判断失误和均衡电路频繁启动等问题，针对此，在分析锂电池极化电压、欧姆内阻、充放电电流对端电压影响特性的基础上，提出基于动态模糊阈值的均衡方法，首先基于模糊算法对端电压阈值进行动态设置，然后据此进行均衡控制操作。实验表明，与传统端电压阈值均衡策略相比，该方法能够有效缩小单体电池之间端电压差异，明显缩短均衡时间。

电池均衡；端电压；动态阈值；模糊算法

0 引言

为了满足新能源汽车大容量、高功率需求，一般将数百节单体电池串并联成组使用。电池均衡控制技术是缓解电池组不一致性的一种有效方法[1]。现有的均衡方法大多将端电压作为均衡控制指标。文献[2]将电压作为均衡标准来判断单体电池的不一致性程度，并在搁置和充放电的不同情况下验证了均衡的效果。文献[3]提出了基于能量转移型均衡电路的模糊 PI 控制方法，用电流和电压作为输入，均衡拓扑结构开关频率作为输出来控制和提高单体电池电压控制精度。文献[4]提出了一种能量转移型均衡方法，采用固定阈值判别单体电池不均衡度，将充放电过程中电压完全一致作为控制目标。文献[5]提出了动态阈值电压均衡策略，其阈值为一次线性关系式，该方法较传统固定阈值均衡策略有效提高了均衡效率，但阈值设置时未充分考虑充放电过程中影响端电压变化的各种因素，其阈值线性关系式的设计合理性还需要商榷。

本文从端电压均衡策略出发,分析充放电过程中电池内阻和充放电流对端电压变化的影响，在此基础上提出了基于模糊动态阈值的均衡方法，运用模糊算法对各种影响因素进行定量分析，对阈值进行模糊运算，并据此进行不一致性判别和均衡操作。实验表明，与传统固定阈值方法相比，本方法有效规避了判别错误性和操作振荡性，提升了均衡系统的效率和效果。

1 端电压与开路电压的动态关系模型分析

1.1 锂电池的等效电路模型(Thevenin模型)[6]

Thevenin电池模型如图1所示，本文为了便于分析，以单体电池放电阶段的各参数变化过程为例进行讨论。如图1所示，UOCV表示开路电压，R0表示欧姆内阻，RP表示极化内阻，UP表示极化电压，在工作电流为ic的情况下，电池的端电压UC可由下式求得

UOCV=UC+icR0+UP

(1)

由式(1)可以看出，开路电压和端电压的关系受到电池充放电时电流、电池内阻的影响。为了准确地估算开路电压和端电压的关系，需要考虑电流和电池内阻在电池充放电过程中对电压的影响。

图1 Thevenin电池模型(放电阶段)Fig.1 Thevenin battery model (discharge stage)

1.2 极化电压和欧姆内阻的过程分析

采用充分静置法来检测极化电压的变化状况。以下数据均为恒流阶段的数据[7]。图2中dis代表电池组放电阶段，ch代表电池组充电阶段。

图2 充放电极化电压变化曲线Fig.2 Polarization voltage variation curve during charge discharge

在电池充放电过程中，当20%≤SSOC≤80%时，极化电压比较小，变化不大；当充放电时SSOC>80%和放电时SSOC<20%，极化电压在短时间内急剧地增大。表明电池在较宽的区域内，内部极化现象不太明显。所以对于电池充放电末期，电池均衡时，不得不考虑极化电压对端电压和开路电压之间关系的影响。

在充放电整个过程中极化电压UP表示如下：

(2)

其中,C为常量，β为在充放电末端随SSOC的动态变化值。

对四个单体电池进行试验，同样选择恒流充电，得出四只单体电池不同SSOC所对应的欧姆内阻值[8]。

图3为锂电池充放电过程中欧姆内阻的变化曲线，图中从上往下四条线代表1号、2号、3号、4号电池的欧姆内阻值。从图3可知，欧姆内阻在整个过程中基本保持不变。在分析开路电压和端电压的关系时，可视为常量。

图3 四只电池不同SSOC所对应的欧姆内阻值Fig.3 The corresponding 4 ohm internal resistance of battery with different SOC

1.3 端电压和开路电压的动态关系分析

基于式(1)可以得到开路电压和端电压的总体变化关系如下[9]：

ΔUOCV=ΔUC+ΔicRi+icΔRi+ΔUP

(3)

其中由于欧姆电阻基本保持不变，所以忽略欧姆电阻变化所带来的影响。进而得到以下公式：

ΔUOCV=ΔUC+ΔicRi+ΔUP

(4)

从式(4)可以看出，单体电池的端电压的变化量不仅直接受到电池开路电压的影响，同时也受到充放电电流和电池内阻的影响。单体电池在不同时间段内相同的ΔUOCV、ΔUC也具有不同的变化程度，在充放电末期，由于极化电压的存在，电池电流不断变化，会出现ΔUOCV≠ΔUC的情况，这会使系统判断电池不一致性出现错误，导致均衡系统进行不必要的均衡操作，增加系统负担，造成能量损耗[10-11]。

由于在一定条件下电池的SSOC和电池的端电压之间存在一定的对应关系，特别是在充放电末期线性对应关系更加直接，所以本文以电池端电压作为电池的不一致性评判指数，最大值均衡法作为控制算法。

2 动态模糊端电压阈值分析与设置

2.1 动态模糊端电压阈值的提出与分析

在电池充放电过程中，检测各个单体电池的电压，设Umax为串联电池组中端电压最高的单体电压值，Umin为串联电池组中电压最低的单体电压值。设定预定电压阈值为ΔUth，Umax-Umin=ΔU，当ΔU≥ΔUth时，均衡系统将启动均衡操作，将电压最高的电池能量释放给串联电池组或者电压最低的单体。

由于电池SSOC和开路电压之间并非线性相关，在20%≤SSOC≤80%时，其变化曲线较为平坦，而在SSOC<20%,SSOC>80%时，其变化较为剧烈，以上内容可总结为以下公式：

(5)

其中K作为一个基于UOCV-SSOC变化曲线的动态近似斜率，在不同的时间段内取不同的数量值。

基于式(5)可以得出：

(6)

从式(6)中可以看出单体电池在不同时间段相同的ΔSSOC的范围内，端电压的变化量ΔUC并不与ΔSSOC是直接的线性对应关系，它受到三种因素(K，Δic，ΔUP)的影响。在20%≤SSOC≤80%阶段，由于极化电压变化比较小，在此区间内主要考虑的因素为动态近似斜率K和充放电电流ic短时间内的变化程度，当充放电电流突然变化时，由于内阻的存在，使得端电压发生较大变化，但单体电池的开路电压短时间内不会发生太大变化，如不考虑电流所带来的影响，将会出现电池不均衡度的判断错误问题。在SSOC<20%和SSOC>80%阶段，不仅要考虑到上面两种因素所带来的影响，还要考虑在此阶段电池极化电压对电池端电压变化所带来的影响，由于极化电压急剧变化，故若忽视其带来的影响，会造成ΔUOCV≪ΔUC，这同样会出现电池不均衡度的判断错误问题[12]。

基于以上分析可知，如图4所示，锂电池的端电压变化程度不仅与电池SSOC有关系，充放电过程中电流的变化和极化电压的变化同样对其也有影响。根据以上因素的分析，为了解决电池不均衡度的判断错误问题，本文提出了动态电压阈值ΔUth的均衡策略。在不同阶段，根据不同的影响因素，设定不同的均衡阈值，以此来判断单体电池是否处于不均衡状态，是否确定开启均衡系统。

图4 影响端电压变化过程示意图Fig.4 Schematic diagram of the influence of terminal voltage variation

2.2 动态模糊端电压阈值的设置

从上文分析可以看出，在电池充放电过程中，电池组受到很多因素的影响且电池参数变化具有非线性以及时变性等特点，因此无法建立精确的数学模型，均衡过程必须保持较高的动态特性。通过对电池端电压三种影响因素的研究发现，单体电池端电压的变化是有一定规律可循的，因此，采用模糊控制算法实现对均衡电压阈值的控制，进而实现电池组充放电的均衡控制。

模糊逻辑控制器(FLC)由控制规则、推理引擎(if…then…)、模糊化以及去模糊化四部分组成，如图5所示。

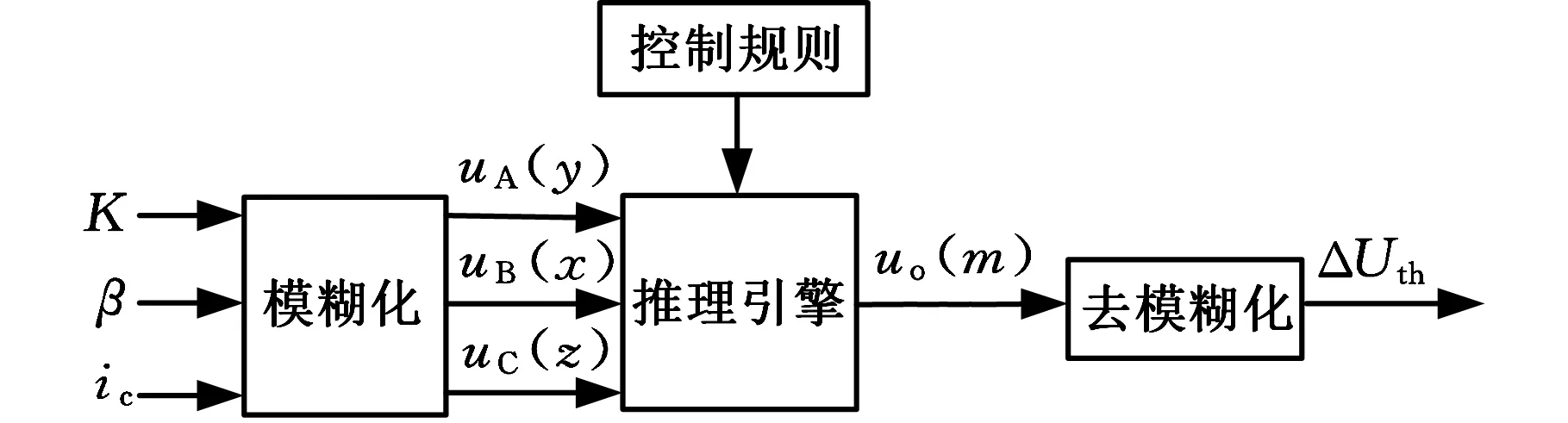
图5 模糊逻辑控制器框图Fig.5 Fuzzy logic controller block diagram

系统的控制目标为在不过放过充的情况下实现电池组的电压均衡，因此采用三输入-单输出的结构。模糊控制器的三个输入为(K，β，Δic)。Δic为电池充放电过程中电流的变化程度。模糊控制的输出量为电池均衡系统的电压阈值ΔUth。输入量经模糊化过程转换为模糊量，控制规则用来描述单体电池均衡算法的知识和过程，基于输入模糊量和控制规则在推理引擎中转化为语言控制值。语言推理结果经非模糊化处理转换为实际的输出值。

从图2可以看出单体锂电池的极化电压整个充放电过程中的主要变化范围为0.1～0.6 V。由于锂电池不同种类的区别，所以其工作电流范围会不同，一般充放电电流的大小用充放电倍率C来表示。根据文献[6]研究发现，对于老化程度不同的锂电池，在无均衡条件下，SSOC在中间阶段每变化10%，开路电压UOCV的变化平均值为20 mV，电池在放电末期[20%,40%]内工作电压的变化均超过25 mV。

故根据上述分析，本文选定β的论域为[0.1，0.6]V、Δic的论域为[0，1C]、而动态曲线斜率值K的论域值为[0.5，6]。ΔUth的论域为[0，0.03]V。进一步定义K、β、Δic及ΔUth的模糊语言变量子集，分别为

K：{L(低)，M(适中)，H(高)}

Δic：{W(弱)，M(适中)，S(强)}

β：{S(小)，M(中)，B(大)}

ΔUth：{S(小)，M(中)，B(大)}

隶属度函数均为三角形函数。

对电池充放电过程的数据进行分析、总结，根据相应的经验，确定电池均衡控制算法的模糊规则如表1所示。

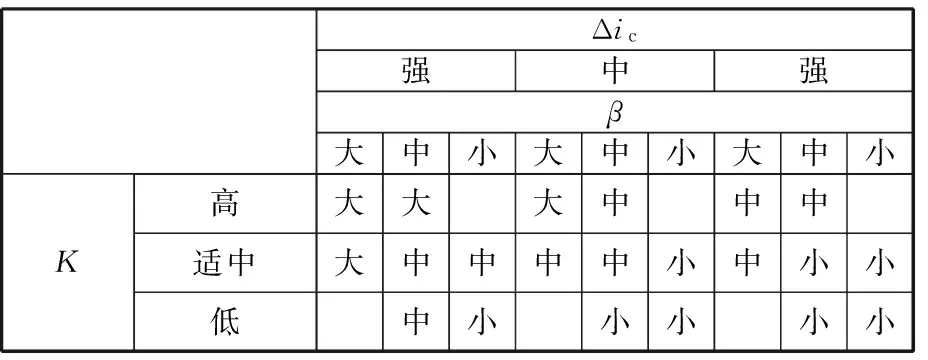
表1 均衡系统模糊控制规则表(输出量为动态阈值ΔUth)Tab.1 Fuzzy control rule table of equilibrium system(the output is dynamic threshold voltage ΔUth)

表1中，模糊控制器的输出量为均衡系统的动态阈值ΔUth根据模糊推理器输入的模糊值分配，制订的21条控制规则。模糊推理过程如下：

(1)模糊化。通过对电池组不同阶段的状态监测和设计好各自的隶属函数，分别计算其对应的模糊输入隶属函数度uAn(K)、uBn(β)、uCn(Δic)。

(2)规则匹配。利用模糊逻辑运算符，用模糊输入隶属度计算规则前件的满足度ωn,即

ωn=min(uAn(K),uBn(β),uCn(Δic))

(7)

(3)模糊推理。根据蕴涵运算符和单条规则uOn(ΔUth)，计算出单条规则的模糊结论，用隶属函数表示为

(8)

(4)结论合成。对输出单条规则的模糊结论进行累加，融合为总的uOn(ΔUth)，即

(9)

(5)去模糊化。对模糊输出应用重心法进行去模糊化，计算出动态阈值ΔUth表达式为

(10)

3 基于动态模糊阈值的均衡控制策略设计

图6示出了均衡控制流程。系统启动后，均衡控制程序开始运行，整个控制流程分为两个部分。首先检测与计算电池组充放电电流变化值Δic和各单体电池的端电压UC，计算电池组平均电压值，判断电池组充放电过程所处阶段，以此来确定K、β，并将其与Δic作为输入参数确定各参数的模糊输入值，根据模糊算法计算动态阈值ΔUth。与此同时根据所检测的各单体电池端电压UC，找出最高电压和最低电压的单体电池，计算电池组极差值ΔU=Umax-Umin，与动态阈值ΔUth进行对比，当ΔU≥ΔUth时，则启动均衡，均衡一段时间后再进入下一次循环，周而复始，当ΔU<ΔUth时则停止。

图6 均衡控制流程图Fig.6 Equilibrium control flow chart

4 实验结果及分析

为了验证本文研究的动力锂电池组均衡模糊控制策略，将该均衡策略集成到课题组自行研制的电池测试平台台架进行放电实验，实验在25 ℃恒温条件下进行。实验选用A12318650磷酸铁锂电池，额定电压为3.3 V，放电截止电压为2 V，充电截止电压为3.65 V，标称容量为1.1 A·h。选用经过循环充放电300次的12节电池进行放电实验。为了可以体现出充放电电流变化值Δic作为模糊控制算法中的输入量参与了运算，使用图7所示的自定义工况对均衡方法进行放电实验检验。将这12节电池分为A、B两组进行实验。其中A组电池使用传统固定电压阈值的均衡策略进行均衡操作，阈值选定为0.025 V。B组电池使用本文研究的动态电压阈值的均衡策略进行均衡操作。动态阈值ΔUth选择范围为(0，0.03)V。实验过程中，首先用智能充电机的预充/大电流/恒压/小电流/脉冲/浮充六个阶段对12节单体电池充满电，再对两组电池进行不同均衡策略下的带电阻负载放电，整个放电实验中采用电压采集模块对各单体电池电压进行采集和记录，任意电池达到放电截止电压(2 V)则停止放电，记录当前电压分布状况以及电池组放出的电量，再对单节电池进行单独放电，记录每节电池剩余电量。

图7 自定义工况放电电流图Fig.7 Discharge current of custom condition

在电池工作初期，启动均衡控制策略，一直到电池工作末期，整个均衡过程中动态阈值变化过程如图8所示，由图8a可见，传统电压阈值均衡策略放电到t=100 min左右时，A组中出现单体电池达到放电截止电压，整组电池就会放电完毕，同时可以看出6节电池在放电过程中电压曲线波动比较大，可控均衡一致的效果较差。而从图8b可知，动态阈值电压均衡策略中放电到t=120 min左右时，B组中出现单体电池达到放电截止电压，放电完毕。6节电池在放电过程中电压曲线相比于A组电池电压曲线波动较小，可控均衡一致的效果较好。

由上述分析可得动态阈值电压均衡策略较传统电压阈值均衡策略延长了电池组放电时间20%，同时减小了电池电压的振荡，避免了单体电池因错误判断其不均衡度而导致反复均衡的情况。

(a)传统电压阈值均衡策略

(b)动态阈值电压均衡策略图8 传统阈值电压和动态阈值电压均衡策略放电实验效果Fig.8 Discharge effect of traditional threshold voltage and dynamic threshold voltage equalization strategy

图9反映了放电截止后电池组A中单体电池电压分布情况，根据表2计算其方差为0.004 166。而图10反映了放电截止后电池组B中单体电池分布情况，根据表2计算其方差为0.003 158，由两组电池电压分布情况对比可知，A组电池电压分布差异大于B组电池电压分布差异，基于模糊控制算法的动态阈值电压均衡策略相比于传统电压阈值均衡策略，电池组电压不一致性较低了24%，能防止电池发生过放现象，提高电池组能量利用率。

图9 放电结束电池组A电压分布(基于传统阈值电压均衡策略)Fig.9 Batterypack A voltage distribution at the end of discharge(based on traditional threshold voltage equalization strategy)

均衡算法放电放出容量比(%)每分钟均衡启停次数传统固定阈值均衡策略852.6动态一次线性阈值均衡策略891.8动态模糊阈值均衡策略941.1

图10 放电结束电池组B电压分布(基于动态阈值电压均衡策略)Fig.10 Battery pack B voltage distribution at the end of discharge (based on dynamic threshold voltage balancing strategy)

实验同时对比了文献[5]所提出的均衡策略，文献[5]中也提出了动态阈值的均衡方法，动态阈值ΔUth=ak+b|ic|+c，其中,a、b、c均是大于0的系数。如表2所示，其中均衡启停次数指单位时间内均衡硬件电路启动和停止的次数和。

表2数据表明，动态模糊阈值电压均衡策略平均每分钟均衡启停次数比文献[5]中提到的动态一次线性阈值均衡策略减少了0.7次，有较好的稳定性，减少了系统负担和造成的能量损耗。其容量利用率比动态一次线性阈值均衡策略提高了5.6%，能够更加有效地利用电池组容量。

因此，上述实验结果可以证明，相比于传统阈值电压均衡策略和文献[5]中动态一次线性阈值均衡策略，利用模糊控制的动态阈值电压均衡策略在放电时间、均衡系统效率上更有优势。

5 结语

本文针对当前传统电压最大值法均衡策略造成均衡判断错误，电路频繁启动等问题，综合考虑电池极化电压、充放电电流变化程度及其对电池端电压变化程度造成的影响提出了基于模糊控制算法的动力电池组均衡策略，测试台实验表明该方案能够有效缩小单体电池之间电压差异，明显缩短均衡时间，降低电池组之间的不一致性。今后的研究工作可以对电池的均衡时间窗口进行研究和对UOCV估算模型进行优化，对电池控制阈值大小和电池均衡波动性之间的关系作细化研究，重点分析电池均衡微观操作过程，在均衡过程中需要重点解决电池均衡状态可达性问题和探讨具体均衡路径，实现参数的优化选择,进一步提升均衡性能。

[1] 韩江洪，王龙飞，刘征宇，等.基于剩余容量的锂离子电池组均衡策略[J].电子测量与仪器学报，2014，28(10): 1047-1052. HAN Jianghong, WANG Longfei, LIU Zhengyu. Equalization Strategy for Lithium Battery Pack Based on the State of Charge [J]. Journal of Electronic Measurement and Instrument，2014，28(10):1047-1052.

[2] 董博,李永东.基于剩余容量估算的快速蓄电池均衡[J].清华大学学报:自然科学版,2012,52(3):374-379． DONG Bo,LI Yongdong．Quick Battery Equalization Based on the State of Charge[J]. Journal of Tsinghua University: Science and Technology,2012, 52 (3):374-379．

[3] 黄勤，严贺彪，林睿，等．锂电池组能量均衡的模糊-PI控制研究[J]．计算机工程，2012,38(8):280-282． HUANG Qin，YAN HeBiao，LIN Rui，et al．Research on Fuzzy-PI Control for Lithium Battery Pack Energy Equalization[J]．Computer Engineering，2012，38(8):280-282.

[4] 邱斌斌，王智弘，李程，等. 电池组用荷电状态均衡充电模糊控制策略[J]. 电源学报，2015,13(2):113-120. QIU Binbin, WANG Zhihong, LI Cheng, et al. Fuzzy Control Strategy for Battery Equalization Charge Based on State of Charge[J].Journal of Power Supply,2015,13(2):113-120.

[5] QI Guoguang, Li Xiangjun, YANG Daiming. A Control Strategy for Dynamic Balancing of Lithium Iron Phosphate Battery Based on the Performance of Cell Voltage[C]//. ITEC Asia-pacific.NewYork:IEEE, 2014:1569952277.

[6] HU Xiaosong,LI Shengbo, PENG Huei. A Comparative Study of Equivalent Circuit Models for Li-ion Batteries[J].Journal of Power Sources,2012,98(5): 359-367

[7] 姚雷，王震坡. 锂离子电池极化电压特[J]. 北京理工大学学报,2014,34(9)：221-226 YAO Lei, WANG Zhenpo. Polarization Characteristics of the Lithiunm-ion Battery[J]. Transactions of Beijing Institute of Technology,2014,34(9)：221-226.

[8] 刘红锐，夏超英.一种新型的电动汽车用电池均衡方法探讨[J].汽车工程，2013，35(10): 934-938. LIU Hongrui, XIA Chaoying. An Investigation into a New Battery Balancing Solution for Electric Vehicles [J]. Vehicle Engineering，2013，35(10): 934-938.

[9] CHO Y，KOR AN A，MIWA H，et al． An Active Currentre Construction and Balancing Strategy with DC-link Current Sensing for a Multi-phase Coupled-inductor Converter[J].IEEE Transactions on Power Electronics，2012,27(4):1697-1705．

[10] CHEN Haoqi, ZHANG Liang. System-theoretic Analysis of a Class of Battery Equalization Systems: Mathematical Modelingand PerformanceEvaluation[J].IEEE Transaction on Vehicular Technology,2015,64(4):1445.

[11] MARKUS E, WERNER R, JUERGEN F. Improved Performance of Serially Connected Li-ion Batteries with Active Cell Balancing Electric Vehicles[J].IEEE Transactions on Vehicular Technology，2011，60(6):2448-2457.

[12] 王占国，文锋，盛大双，等．新型充放电均衡一体化电池管理系统研究[J]．电子测量与仪器学报，2012，26(5):431-436． WANG Zhanguo, WEN Feng, SHENG Dashuang, et al．New Battery Management System of Integrated Charging and Discharging Balance[J].Journal of Electronic Measurement and Instrument,2012,26(5):431-436.

(编辑 王艳丽)

Optimization of Battery Equalization Strategies Based on Dynamic Fuzzy Threshold

LIU Zhengyu1，2MA Yadong1SUN Qing1TANG Wei1

1.School of Mechanical and Automotive Engineering，Hefei University of Technology，Hefei, 230009 2.Engineering Research Center of Safety Critical Industry Measurement and Control Technology，Ministry of Education，Hefei,230009

A fixed terminal voltage threshold simply took as power battery equalization control indicators, which might lead to equalization judgment errors and equalization circuit on-off frequently. To solve above problems, based on the impact analyses of lithium battery polarization voltages, Ohm internal resistance, charge-discharge current on the terminal voltage characteristics, a dynamic fuzzy threshold equilibrium method was proposed. First of all, based on the fuzzy algorithm, terminal voltage thresholds were dynamically setted, then equalization control operations were carried out. Experimental results show that compared with the threshold voltage of the traditional equilibrium strategies, this method may effectively reduce monomer battery terminal voltage differences ，obviously shorten the equilibrium time.

battery equalization; terminal voltage; dynamic threshold; fuzzy algorithm

2016-05-15

国家国际科技合作专项(2012DFB10060)

TP273;TN86

10.3969/j.issn.1004-132X.2017.05.019

刘征宇，男，1979年生。合肥工业大学机械工程学院副教授。主要研究方向为新能源汽车能量系统建模与控制。发表论文10余篇。E-mail：liuzhengyu@hfut.edu.cn。马亚东,男，1991年生。合肥工业大学机械工程学院硕士研究生。孙 庆，男，1991年生。合肥工业大学机械工程学院硕士研究生。王雪松，男，1990年生。合肥工业大学机械工程学院硕士研究生。