振动拉削系统振幅衰减特性分析与实验研究

蒙 臻 倪 敬 武传宇

1.浙江理工大学机械与自动控制学院,杭州,3100182.杭州电子科技大学机械工程学院,杭州,310018

振动拉削系统振幅衰减特性分析与实验研究

蒙 臻1倪 敬2武传宇1

1.浙江理工大学机械与自动控制学院,杭州,3100182.杭州电子科技大学机械工程学院,杭州,310018

为了探究振动拉削中导致激振幅值衰减的主要因素，以双伺服阀电液激振拉削设备为研究对象，综合考虑双阀电液激振系统动力学特性，以及拉刀多齿接触效应、工件尺寸参数等影响下的动态拉削力特征，建立了振动拉削过程中的激振系统模型；再分别通过理论计算及系统实验，对比研究了电液激振器在非线性负载扰动下实际输出力和输出位移的衰减波形，为振动拉削激振系统参数优化提供理论指导和实验依据。实验结果分析表明：振动频率是导致系统振幅衰减的主要因素，而动态拉削力通过影响激振缸活塞的运动特征使得输出波形的峰值衰减，甚至使位移振幅趋向于0。

双阀激振；拉削负载；激振特性；幅值衰减

0 引言

振动加工与传统加工相结合，可有效改善加工质量，延长刀具使用寿命[1]，在高附加值材料加工及超精密加工等方面有巨大的发展潜力。由于电液激振装置具有低频特性好、推力大及过载易保护等优点[2]，故笔者将电液激振引入拉削加工工艺。在研究过程中发现，电液激振系统在动态拉削力影响下的幅值衰减特性，是实现匹配振动拉削负载、优化振动拉削电液激振系统工艺参数，以及实现稳定可行的振动拉削工艺的关键所在。

目前振动拉削方面公开发表的文献较少，但已有不少学者针对电液激振器在负载扰动下的输出性能开展研究，先后发表了相关的理论分析和实验研究成果。如浙江工业大学的阮健团队，基于二自由度的高频激振阀[3-4]和颤振型液压缸[5-7]，研究电液激振系统的输出特性及影响激振缸输出力和位移幅值的主要因素，他们在构建电液激振器动力学模型时，与ZHAO等[8]一样，将外界扰动等效为水平放置的弹簧质量块系统，以求解系统的输出波形；ATHANASATOS等[9]在用伯德图研究振动疲劳测试系统的输出特性时，构建了悬臂梁结构的负载模型； 文献[10-13]为了研究智能控制算法对液压振动平台稳定性的修正效果，针对负载部分构建了多自由度弹簧-质量块数学模型。但上述文献所涉及的研究内容，一方面系统负载或扰动都是时不变的，而拉削负载具有较强的非线性和时变特性；另一方面只探讨了电液激振器的输出特性与输入信号之间的关系，而忽视了负载对激振性能的衰减作用。因此，在拉削负载耦合特性影响下的电液激振输出特性还有待于进一步研究。

本文以双伺服阀电液激振拉床为研究对象，基于动态拉削力与激振输出力的强耦合关系，引入液压伺服理论和牛顿动力学体系，建立了振动拉削系统的电液激振特性模型，并采用理论分析计算和实际系统测试的方法，研究了动态负载影响下双阀激振系统输出位移和输出力的规律特性，最终为振动拉削工艺提供了合理的激振参数选择及优化方法。

1 振动拉削系统

振动拉削加工系统原理如图1所示，主要由电液激振装置、拉削主油缸、导向柱、导套及拉刀等部件组成，拉削主油缸与激振装置分别采用独立的油源供能。各部件的具体安装方式为：拉削主油缸活塞杆与溜板通过螺纹及紧定螺钉固连一体；溜板上有对称安装的轴套，使其可在导向柱上滑动；溜板上还安装有如图2所示的电液激振装置，其活塞杆直接与刀夹头螺纹连接，而刀夹头与拉刀则通过紧定插销和紧定螺栓固连一体；拉刀通过安装在端板上的导向套直接从待加工工件的内孔穿过。

图1 振动拉削系统示意图Fig.1 Schematic diagram of vibration broaching system

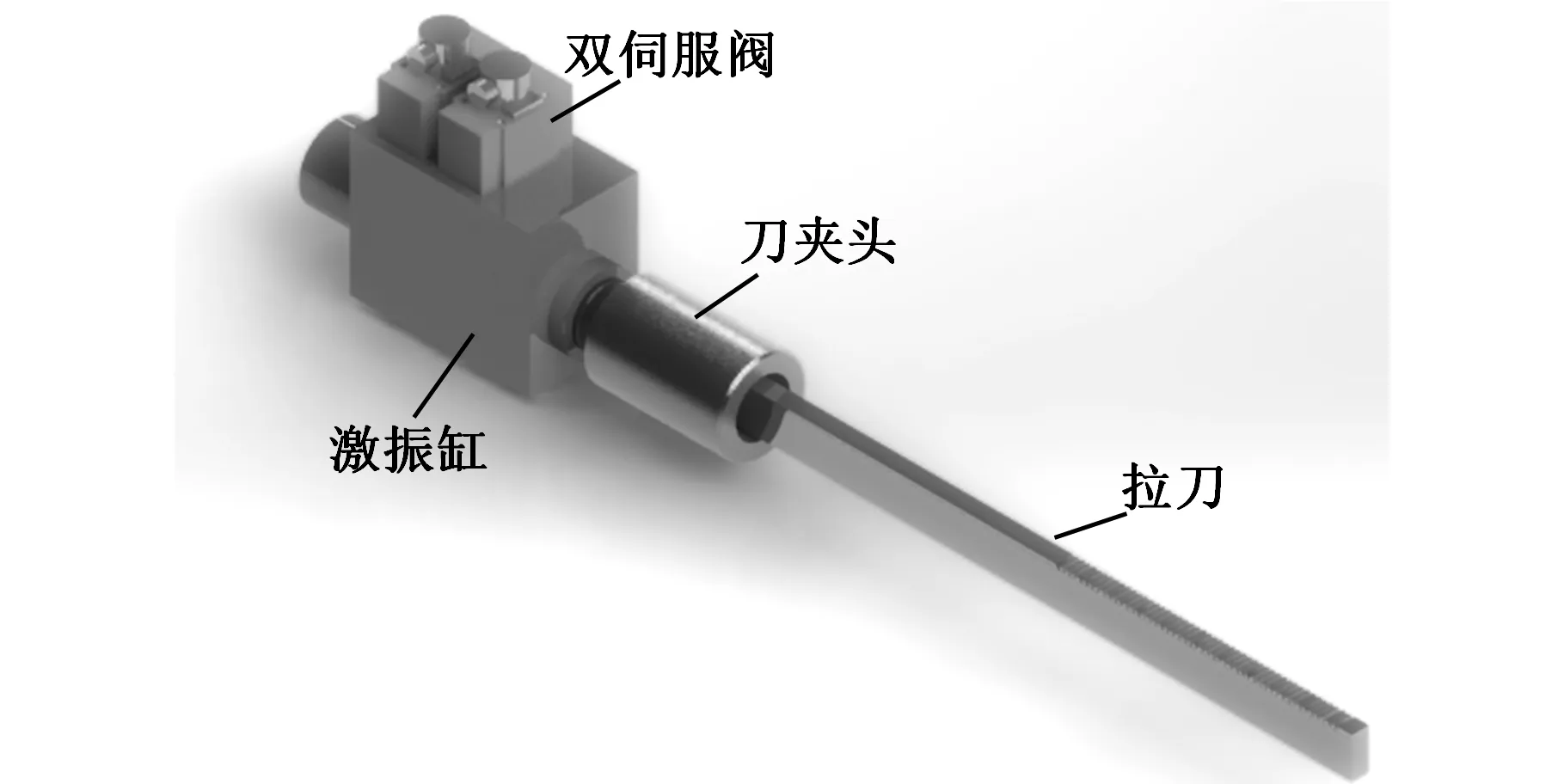
图2 双阀电液激振系统示意图Fig.2 The dual-valve excitation system

该系统的工作过程为：在拉削主油缸驱动拉刀沿导向柱以速度vc做直线匀速运动时，电液激振装置输出周期性往复运动vt，使拉刀运行具有复合的运动形式，将传统的接近→接触→拉削过程转换为接近→接触→拉削→脱离→再接近的循环过程，使连续的拉削过程离散为脉动式切削过程。由于每次接触工件时的材料去除量相对传统加工过程要大为减少，因此降低了平均拉削负载。同时，拉刀动态接触工件，减小了加工应力的集中程度，使整个拉削过程更为平稳。而根据相关研究文献，只有当振动速度vt大于切削速度vc时才能形成上述脉动式切削过程。

对振动拉削的激振系统来说，激振力和振幅是影响拉削效果的重要因素，因此，通过研究实际拉削过程中相关参数的衰减特性，可为振动拉削工艺所需的稳定可靠的激振系统提供设计思路及优化方向。

2 激振系统动力学模型

双阀控电液激振装置的动力学原理如图3所示，图中，pP、pT、p1、p2分别为油源供油、油源回油、液压缸无杆腔和有杆腔的压力，MPa；pPi、pTi、pi1、pi2分别为第i(i=1, 2)个伺服阀的P口、T口、A口和B口的压力，MPa；qP、q1、q2分别为油源供油、进入无杆腔和流出有杆腔的流量，mL；qPi、qi1、qi2分别为流经第i个伺服阀P口、A口和B口的的流量，mL；A1、A2分别为激振缸无杆腔和有杆腔的面积，mm2；xvi为第i个伺服阀阀芯位移，mm；xp为激振缸活塞位移，mm。根据图3所示，阀芯位移xvi向左为正；活塞位移xp向右为正。

图3 振动辅助拉削简图Fig.3 Simplified diagram of vibration-assisted broaching

拉刀与激振缸活塞杆为刚性连接，则根据牛顿-欧拉法，振动拉削过程中激振系统的动力学特性可描述为

(1)

式中，M为折算到活塞上的总质量，kg；C为电液激振系统的总阻尼系数；K为系统的等效弹簧刚度；Fp为输出的激振力，N；Fc为拉削负载力，N；Ff为摩擦力，N。

由式(1)可知，激振系统的输出特性(输出位移和输出力)与拉削负载特性间存在耦合关系,因此，本文首先针对空载条件下的双阀电液伺服系统特性展开研究，再引入拉削负载模型，探求拉削负载扰动对激振系统振幅衰减特性的影响。

2.1 双阀系统模型

根据如图3所示的流体运动特性，双阀激振系统可通过伺服阀负载流量模型、多路流量耦合模型及阀控非对称缸模型来综合描述。

(1) 伺服阀负载流量模型如图3所示，伺服阀阀芯换向运动时，阀口的流量方程可表示为[14]

(2)

(3)

式中，Cd为阀的流量系数；wi为第i个阀的面积梯度，mm；ρ为油液的密度，kg/m3。

(2) 流量耦合模型采用如图3所示的并联伺服阀设置方式，在流体交互运动过程中，会产生多流道间的汇流特性，则进出激振缸的流量可表示为

(4)

(5)

(3) 非对称缸负载流量模型，激振缸工作时，活塞处于高速换向运动状态，可忽略泄漏对于流量的影响，则激振缸两腔的流量连续性方程可表示为

(6)

式中，V1和V2分别为激振缸无杆腔和有杆腔的容积，mm3；βe为有效容积模数，MPa。

(4) 激振缸系统输出力特性，激振缸的输出力与两腔的压差直接相关， 即

Fp=A1p1-A2p2=ALpL

(7)

式中，AL为激振缸负载面积，mm2；pL为激振缸负载压力，MPa。

因此，综合式(4)～式(7)，激振缸输出力特性可描述为

xvi>0时

(8)

xvi<0时

(9)

2.2 拉削负载模型

拉削过程实质上是拉刀刀齿逐次接触工件的过程，如图4所示。当拉刀以速度vc加工工件时，刀具前后齿齿升量的差值相当于进刀量，因此拉削过程只有切削运动，而无进给运动。由于齿升量不同，拉刀分为粗拉区(A)、精拉区(B)和修形区(C)，因此拉削还可实现粗加工和精加工一次加工成形。图中参考线s为过拉刀第1齿齿刃且与拉刀底面平行的直线；第i个齿齿刃与参考线s的距离hi即是该齿的齿升量，mm；p为相邻两齿的间距，mm；d为工件加工长度，mm；Fci为第i个齿的切削力，N。

图4 拉削负载示意图Fig.4 Schematic diagram of broaching

由图4可知，若齿间距p为恒值，则拉削力Fc与参与拉削的齿数n和拉削速度vc直接相关。其中同时参与拉削的齿数nm与齿间距p和筒状工件长度d相关，即

(10)

拉刀单齿的切削力Fci可表示为[15]

Fci=λiklilwi

(11)

式中，λi(i=1,2,…,n)为与刀齿前角等因素有关的修正系数，其值可近似表示为cosαi，αi为第i个刀齿前角；kli为作用在第i个刀齿单位长度切削刃上的力，N/mm；lwi为第i个刀齿切削宽度，mm。

根据文献[15]的经验数据，单位拉削力kli与齿升量hi及工件材料相关，即

(12)

式中，σb为材料的抗拉强度。

拉刀刀齿渐次接触工件，由后续刀齿的齿升量形成新的背吃刀量。相邻刀齿接触工件的时间间隔为ti=p/vc。根据键槽拉刀上述切削特性，在如图5所示的筒状工件上加工键槽时，各刀齿的拉削宽度lwi将随时间变化，有

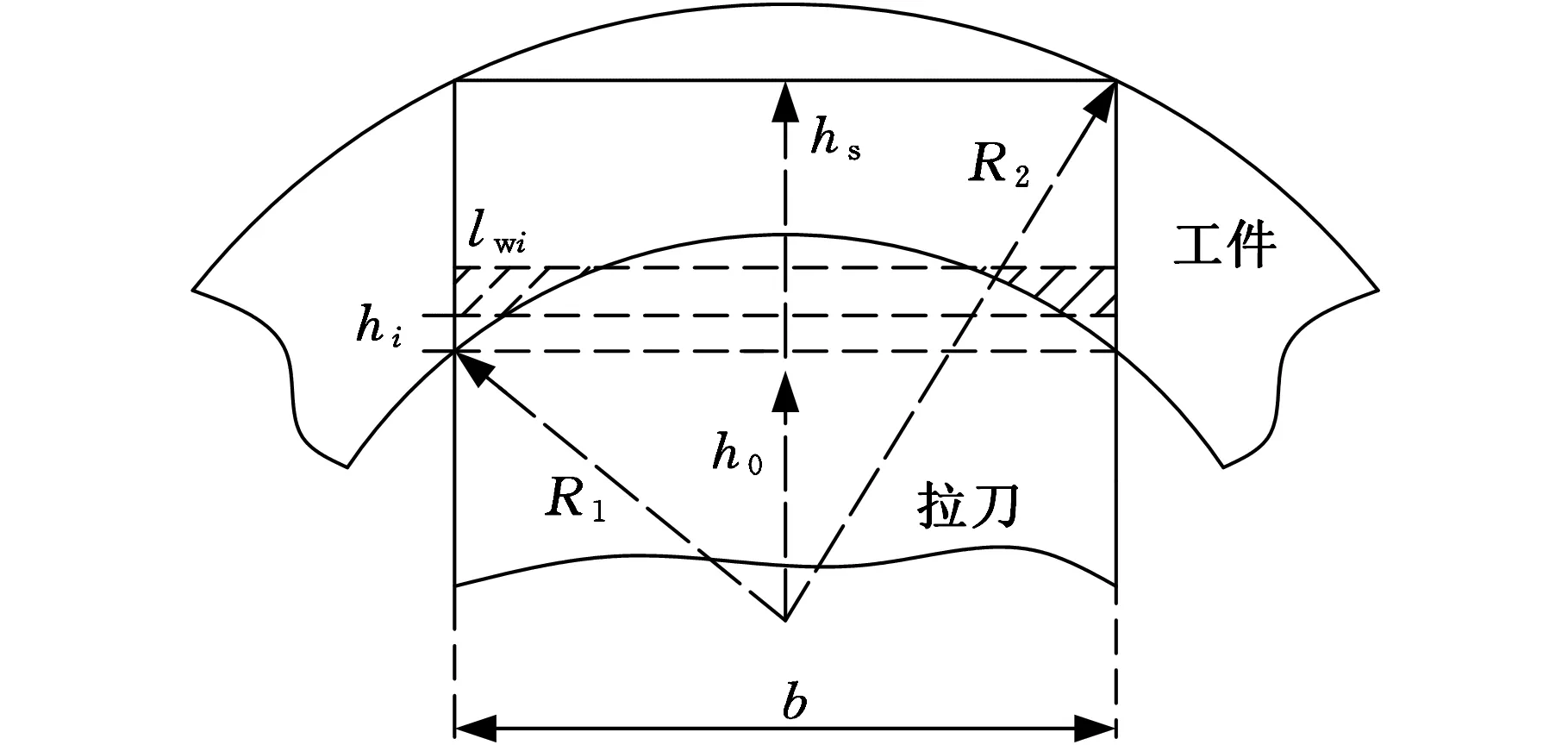
图5 拉削宽度示意图Fig.5 Schematic diagram of broaching width

(13)

t1=(R1-h0)ti/hit2=(hs-h0)ti/hi

式中，h0为刀齿刚接触工件时的初始高度；hs为刀齿切断工件时的最终高度；b为刀齿的宽度；R1为筒状工件的内径；R2为筒状工件的外径。

结合拉削过程中的刀齿数与工件的接触情况，则拉削负载动特性模型Fc(t)可描述为

Fc(t)=

(14)

式中，t0为第1个齿接触到第nm个齿接触的时间。

2.3 系统模型分析

由激振系统运动特性及刀齿拉削过程可知，只有当激振方向与切削方向相同时，拉削负载才会显著影响激振系统输出性能。因此综合式(8)、式(9)和式(14)，双阀激振动力学特性模型可表示为

(15)

其中，当xp>0时，α=0；当xp<0时，α=1。

由式(15)可知，图1所示的振动拉削系统激振力和振幅与阀芯位移及动态拉削力相关。在激振状态下，控制信号为近似简谐波信号，则阀芯位移主要受激振信号频率影响，因此，主要通过变化的激振频率及拉削力对系统激振力和振幅衰减特性的影响展开实验研究。

3 实验方案设计

3.1 实验设备及材料

本文提出的振动拉削系统实物如图6所示，主要由电液激振系统、拉削系统和电控系统组成。

图6 实验系统示意图Fig.6 The experimental system

电液激振系统油源最大工作压力为15 MPa，最大工作流量为100 L/min；激振缸活塞、活塞杆直径及行程分别为80 mm、50 mm及10 mm；激振阀为Rexroth三位四通伺服阀。拉削系统最大拉削力为50 kN，拉削行程为800 mm，最大拉削速度为6 m/min；拉削系统其他参数如表1所示。电控系统的激振控制器为SIMENS S7-300PLC系列的CPU314，包含了IO模块及四通道D/A模块，其中D/A模块与伺服阀信号连接，采用定时中断的方式发送阀芯控制信号；数据采集控制器为S7-300PLC同系列的CPU313C，通过其集成A/D模块实现激振缸压力及位移信号采样，采样周期为2 ms。激振缸工作压力数据通过2个PTH503压力传感器(量程为0～15 MPa，综合精度为0.5% FS，输出信号为4～20 mA，频率响应为5 ms)从无杆腔和有杆腔采样获得；激振缸位移数据通过HLG103AC5激光位移传感器(量程为±4 mm，分辨力为0.5 μm，线性度为±0.1% FS，输出信号为4～20 mA) 从激振缸活塞杆获得。其他主要参数如表1、表2所示。

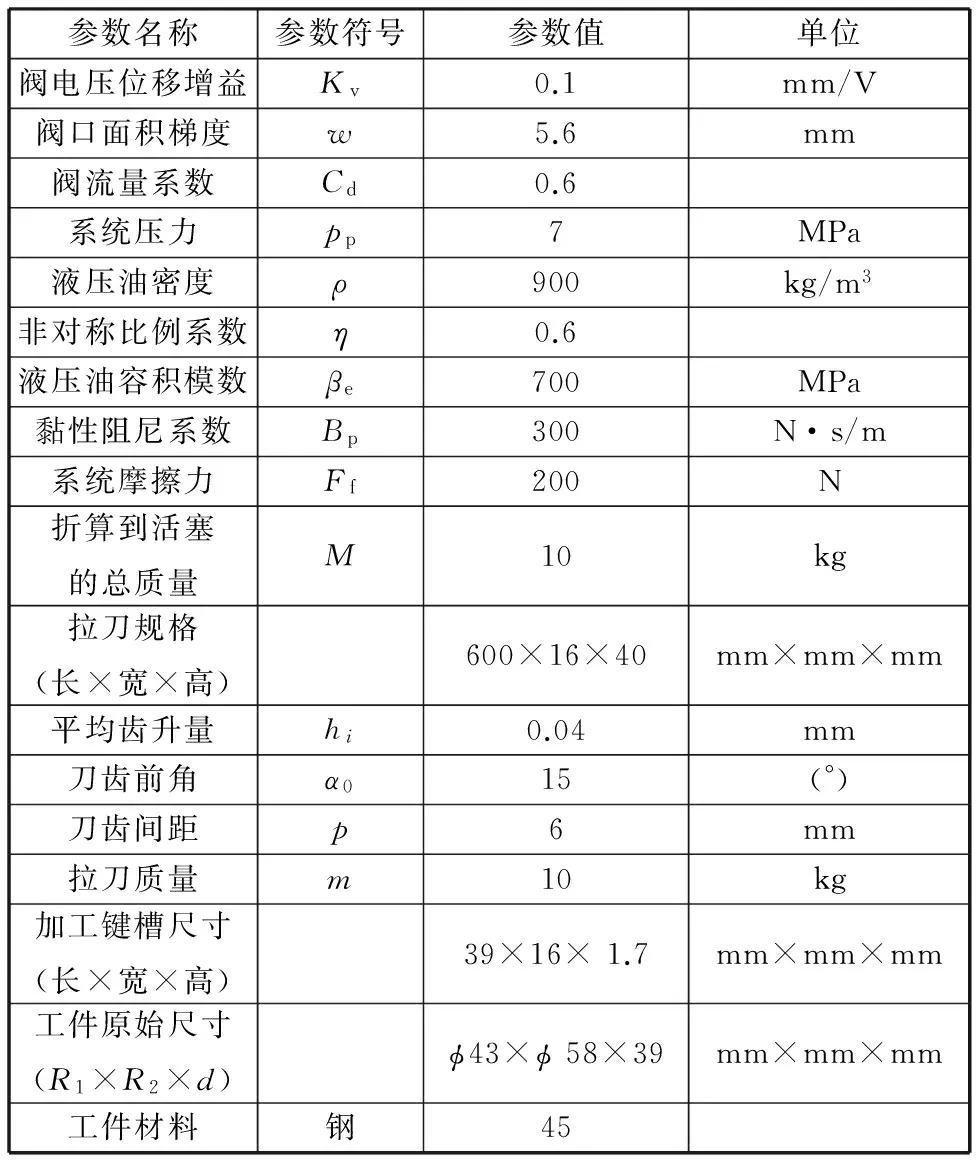
表1 振动拉削系统主要参数表Tab.1 Main parameters of dual-valve excitation system

3.2 实验方法

实验主要分为两个部分:①空载激振实验。本实验中拉削速度vc为拉床的固定拉削速度值44 mm/s；通过电控系统获取激振缸压力和激振缸输出位移数据。实验中，激振信号频率设定为

表2 振动拉削系统主要元件表Tab.2 Major component of vibration broaching system

10 Hz，20 Hz和50 Hz三挡，每挡频率下运行1min/次，重复运行20次。②拉削激振实验。本实验基本工况与空载实验一致，同样设定了三挡激振频率，每挡频率下拉削钢制工件20次，共60组实验。

4 结果与讨论

4.1 输出力衰减特性

图7所示为激振缸输出力幅值的仿真计算结果，表示随激振频率和拉削负载变化，激振缸输出力幅值的分布情况。经仿真计算，拉削力在整个拉削过程中在0～9.8 kN间递增变化。如图7所示，随激振频率提高，输出力幅值下降得十分明显；而随拉削负载变化，输出力幅值在某区间(4～6 kN)会出现较明显的下降。

图7 激振缸输出力仿真曲线图Fig.7 The simulation results of output force by excitation system

图8所示为激振缸输出力幅值的实测结果，横坐标为拉削过程时间(10 s)。如图8所示，在拉削时，初期输出力平均峰值分别为：11.23 kN(10 Hz)，6.40 kN(20 Hz)以及1.12 kN(50 Hz)；当拉削进行到6～8 s时，平均峰值分别下降了26.1%(10 Hz)，23.4%(20 Hz)以及39.3%(50 Hz)。这验证了仿真分析结果，即拉削力递增的时变特性导致输出力幅值跃变。但实测结果发现，当拉削力幅值与激振缸输出力幅值之比较小时，对实际激振系统的容腔压力特性的影响不明显，因此若增大激振缸的输出力幅值范围，在拉削过程中可能不会出现激振力幅值跃变的现象。

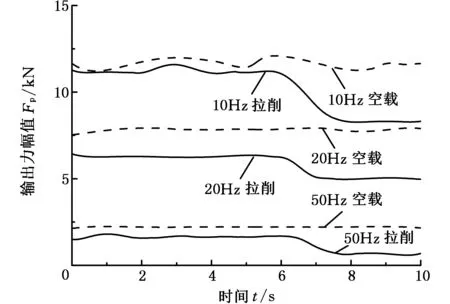
图8 激振缸输出力实测曲线图Fig.8 The experimental results of output force by excitation system

4.2 输出位移衰减特性

图9所示为激振缸输出位移幅值的仿真计算结果，表示随激振频率和拉削负载变化，位移幅值的分布情况。如图9所示，随激振频率提高，输出位移平均幅值降低；随拉削负载增大，输出位移平均幅值也在下降。

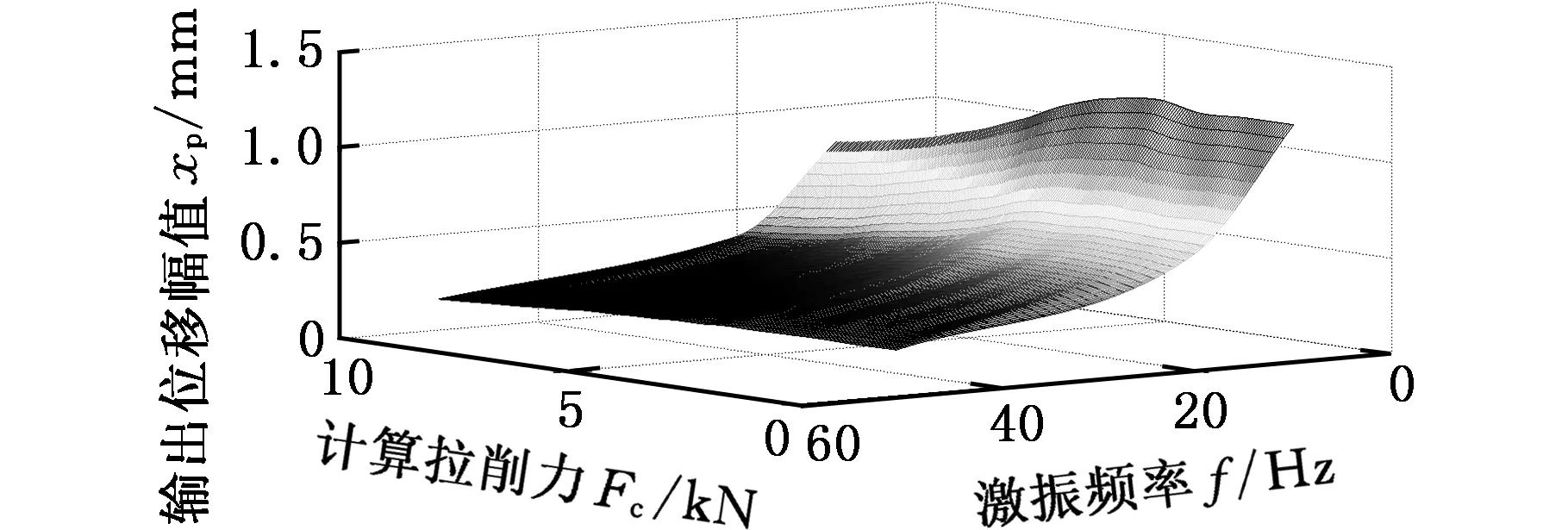
图9 激振缸输出位移仿真曲线图Fig.9 The simulation results of output displacement by excitation system

图10所示为激振缸输出位移幅值的实测结果。如图10所示，在拉削时，初期输出位移平均峰值分别为：1.38 mm(10 Hz)，0.26 mm(20 Hz)以及0.07 mm (50 Hz)；当拉削进行到6 s后，峰值迅速衰减为0。

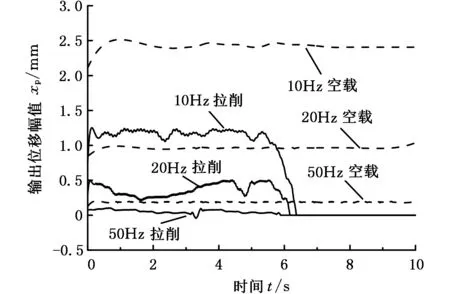
图10 激振缸输出位移实测曲线图Fig.10 The experimental results of output displacement by excitation system

4.3 激振参数敏感性分析

4.3.1 激振频率影响分析

分别对比激振缸输出力和输出位移的仿真与实测曲线可以得到，激振频率是影响系统幅值衰减的主要因素。其原因在于激振频率实质上代表了阀芯开启时间，也就是流向激振缸容量的流量，而容腔压力相对输入流量是一惯性环节，因此随着阀芯切换时间缩短，其输出力增值也大幅下降。因此，若能在相同开启时间内，增加阀体数量(本文已采用了双阀并联供能)，提高输出流量，即可相对减缓频率提高导致的幅值衰减效应。此外，激振频率对于输出位移的稳定性也有一定影响。这是因为振动拉削时，激振缸输出与脉冲式切削运动相互耦合，使得振动位移幅值会发生“漂移”现象；而由于时滞性，压力变化并不能直接反映脉冲式接触过程，因此，若不能对输出位移进行反馈补偿，会影响振动拉削系统的稳定性，甚至反作用于拉削效果。

4.3.2 动态拉削力影响分析

对比上述实验结果可以得到，激振缸输出力特性直接决定了其输出位移特性。根据仿真计算分析，动态拉削力具有较强的非线性和时变特性，它阻碍了激振缸容腔体积的变化，降低了激振缸瞬时速度，影响了激振缸输出力幅值的稳定性，也是限制输出位移幅值的原因之一。当拉削力逐渐大于激振缸输出力时，激振位移幅值衰减为0，此时，振动系统不是依靠位移幅值变化而是由容腔压力波动产生振动输出，因此，为了得到稳定的输出力和输出位移，一方面需要改善激振系统的固有特性，提高其空载输出力幅值范围，另一方面则需要根据脉冲式拉削特性，设置蓄能设备，或以差动的方式为激振缸供能，强制提高脉冲式接触时的输出力峰值。

4.3.3 其他参数的影响

文中未讨论的激振系统其余参数还包括激振缸尺寸参数、激振油源压力及激振信号幅值等。其中，激振缸的尺寸参数影响了它的固有特性；激振系统的油源压力则影响了激振系统输出力的峰值；激振信号幅值与阀芯开口面积及切换峰值相关，对激振控制系统来说，可通过实时调整激振信号幅值，来稳定激振位移幅值。

5 结论

(1)本文综合考虑了双阀电液系统耦合流量特性和拉削负载动特性，构建了振动拉削过程中的电液激振器动特性模型，基于理论分析计算和实际系统测试，研究了激振器输出力和输出位移的衰减特性。

(2)仿真与实验结果表明，本文建立的电液激振模型能较好地描述拉削过程中激振器的输出特性，可为实际振动拉削加工中，激振器相关参数和结构的优化设计提供良好的理论支撑与技术指导。

(3)激振频率是导致激振系统输出幅值衰减的主要因素，当激振频率为50 Hz时，与10 Hz时的输出力幅值相比平均下降了80%左右；输出位移幅值平均下降了90%左右。

(4)动态拉削力也是限制输出位移幅值的重要因素。当拉削力接近激振系统输出力极限时，输出位移幅值会衰减为0。

(5)此外，根据所构建的系统模型推断，影响振幅衰减特性的因素还包括激振缸尺寸参数、激振油源压力及激振信号幅值等。

[1] 隈部淳一郎. 精密加工振动切削基础与应用[M]. 北京：机械工业出版社，1985. KUMABE J. Precision Machining Vibration Cutting (Fundamentals and Applications)[M]. Beijing: China Machine Press,1985.

[2] 吕云嵩，郭均政，柯广云.变量飞轮脉动激振液压振动系统的建模与仿真[J]. 中国机械工程，2015，26(23)：3150-3155. LYU Yunsong，GUO Junzheng，KE Guangyun. Modeling and Simulation of Hydro-vibration System Assisted by Variable Inertia Flywheel Pulsation[J]. China Mechanical Engineering，2015，26(23)：3150-3155.

[3] 李伟荣，阮健，任燕，等. 2D阀单出杆激振缸低频特性研究[J]. 中国机械工程，2014，25(1)：97-102. LI Weirong， RUAN Jian， REN Yan，et al. Research on Low-frequency Characteristics of One -pole Vibration Cylinder Controlled by 2D Valve[J]. China Mechanical Engineering，2014，25(1)：97-102.

[4] REN Y， RUAN J， JIA W A. Output Waveform Analysis of an Electro-hydraulic Vibrator Controlled by the Multiple Valve[J]. Chinese Journal of Mechanical Engineering，2014，27(1)：186-197.

[5] 邢彤，李修武，马宏杰，等. 液压颤振器的谐振特性研究[J]. 中国机械工程，2014，25(8)：1071-1074. XING Tong，LI Xiuwu，MA Hongjie，et al. Study on Resonance Characteristics of Hydraulic Excited Flutter Device[J]. China Mechanical Engineering，2014，25(8)：1071-1074.

[6] 马宏杰，邢彤，付亮. 新型高频电液颤振器的振动研究[J]. 流体传动与控制，2013(5)：37-40. MA Hongjie， XING Tong， FU Liang. Research of the Vibration on a New Type of High Frequency Electro-hydraulic Flutter[J]. Fluid Power Transmission and Control，2013(5)：37-40.

[7] 李修武，邢彤，靳德峰. 液压颤振器的流固耦合振动研究[J]. 流体传动与控制，2013(3)：12-16. LI Xiuwu， XING Tong， JIN Defeng. Study on Fluid-structure Interaction Vibration of Hydraulic excited Vibrator[J]. Fluid Power Transmission and Control，2013(3)：12-16.

[8] ZHAO J B， WANG J Z， WANG S K. Fractional Order Control to the Electro-hydraulic System in Insulator Fatigue Test Device[J]. Mechatronics，2013,23：828-839.

[9] ATHANASATOS P， COSTOPOULOS T. Proactive Fault Finding in a 4/3-way Direction Control Valve of a High Pressure Hydraulic System Using the Bond Graph Method with Digital Simulation[J]. Mechanism and Machine Theory，2012，50：64-89.

[10] SHEN G， ZHU Z C， ZHANG L， et al. Adaptive Feed-forward Compensation for Hybrid Control with Acceleration Time Waveform Replication on Electro- hydraulic Shaking Table[J]. Control Engineering Practice，2013，21：1128-1142.

[11] NARUTOSHI N. Acceleration Trajectory Tracking Control for Earthquake Simulators[J]. Engineering Structures，2010，32：2229-2236.

[12] PEDRO J O， DANGOR M， DAHUNSI O A， et al. Intelligent Feedback Linearization Control of Nonlinear Electrohydraulic Suspension Systems Using Particle Swarm Optimization[J]. Applied Soft Computing， 2014，24：50-62.

[13] STOSIAK M. Vibration Insulation of Hydraulic System Control Components[J]. Archives of Civil and Mechanical Engineering，2011，6(1)：237-248.

[14] 梅里特 H E. 液压控制系统[M]. 陈燕庆，译.北京：科学出版社，1976. MERIT H E. Hydraulic Control System[M]. CHEN Yanqing, Trans. Beijing: Science Press, 1976.

[15] 袁哲俊，刘华明. 金属切削刀具设计手册[M]. 北京：机械工业出版社，2008. YUAN Zhejun, LIU Huaming. Handbook of Metal Cutting Tool Design[M]. Beijing: China Machine Press,2008.

(编辑 王艳丽)

Analysis and Experimental Study of Amplitude Attenuation Characteristics of Vibration Broaching Systems

MENG Zhen1NI Jing2WU Chuanyu1

1.School of Mechanical Engineering and Automation, Zhejiang Sci-Tech University,Hangzhou,310018 2.School of Mechanical Engineering, Hangzhou Dianzi University, Hangzhou, 310018

In order to investigate the major factors of amplitude attenuation during vibration broaching processes, a novel dynamic model of excitation system was established by considering the dynamic characteristics of dual-valve system, the broaching forces affected by the multi cutter tooth and workpiece size parameters. Then, the output waveforms of electro-hydraulic exciter with nonlinear disturbance were studied by the results of numerical simulations and system experiments, which may provide some theoretical references and laboratory evidence for optimizing parameters of the exciter system. The results show that the vibration amplitudes of exciter are mainly limited by the excited frequency. The peak values of waveform are reduced by dynamic broaching forces, which mainly affects the movement characteristics of cylinder piston. Because of that, the displacement amplitudes may tend to zero.

dual-valve excitation; broaching force; vibration characteristics; amplitude attenuation

2016-04-18

国家自然科学基金资助项目(51375129)；浙江理工大学521人才培养计划资助项目

TH137；TG57

10.3969/j.issn.1004-132X.2017.05.003

蒙 臻，男，1986年生。浙江理工大学机械与自动控制学院博士研究生。主要研究方向为电液激振及应用。发表论文4篇。E-mail：mengzhen0601@126.com。倪 敬，男，1979年生。杭州电子科技大学机械工程学院教授。武传宇(通信作者)，男，1976年生。浙江理工大学机械与自动控制学院教授、博士研究生导师。