基于三坐标测量机双参数向自适应测量自由曲面
2017-03-14何雪明李咏平武美萍
何雪明 李咏平 武美萍 张 荣
1.江苏省食品先进制造装备技术重点实验室,无锡,2141222.江南大学理学院,无锡,214122
基于三坐标测量机双参数向自适应测量自由曲面
何雪明1李咏平1武美萍1张 荣2
1.江苏省食品先进制造装备技术重点实验室,无锡,2141222.江南大学理学院,无锡,214122
提出一种基于三坐标测量机的双参数向自适应测量自由曲面方法。CMM手动测量被测曲面边界点后,连接点生成可测区域,由可测区域自动拓扑生成几条均布初始扫描线以及每条扫描线的均匀初始点,对于U向的各条扫描线,CMM在自动测完初始点后,不断拟合已测点为B样条曲线,由曲线末端曲率自适应预测下一测点并指导CMM自动测量。测完初始扫描线后拟合已测点云为B样条曲面,由曲面V向边界最大曲率自适应确定下一扫描线位置,并进行该条扫描线U向自适应测量,重复这一过程直至曲面测量完毕。测点可随被测曲面自身曲率变化特性而疏密分布,曲率变化大的重要特征区域分布密集,曲率变化小的非重要区域分布稀疏,既保证了重要特征点不会遗漏又避免了数据冗余。理论曲线曲面自适应测量实验结果表明该方法测量精度可达微米级,实例零件应用验证了该方法的可行性。
自由曲面;三坐标测量机;双参数向;自适应测量;全自动
0 引言
自由曲面无规律,无法像规则曲面那样利用解析函数来描述,因此具有自由曲面特征零件的高精度测量一直是研究难点[1]。三坐标测量机(coordinate measuring machine,CMM)的高测量精度使其在点的测量上具有很大优势,实际测量过程中,三坐标测量机的测量精度要比激光扫描仪的测量精度高一个数量级,逆向工程中多采用CMM作为高精度数据采集工具[2]。在自由曲面CMM测量中,测点等间距采样最先被提出,这是一种简单易实现的方法[3]。然而等间距采样在曲面起伏变化剧烈的情况下,需缩短间距以保证曲面特征不会丢失,但是这会大幅度增加数据采集的工作量。
为寻求合理的测点测量规划方式,国内外学者开展了广泛而深入的研究。LI[4]提出了等弧长的采样方法,通过输入关键点的坐标数据,并实时输入曲面形状参数来确定网格的间距,从而实现基于曲面扫描线曲率的自适应网格划分,实现等弧长采样测量。KIM等[5]提出三角自适应的曲面测量方法,首先对曲面实施等间距初步采样,然后根据初测结果,决定是否需要实施进一步的测量。ZHANG等[6]提出将神经网络应用于曲面测点的确定,综合考虑零件尺寸、公差和工艺等因素,但该方法的弊端是应用对象单一,只能针对孔曲面,且需要做大量试验,以形成各种参数的数据库供调用。何雪明等[7-8]提出了曲线曲率连续的自适应测量法,利用高次Bézier曲线拟合已测点,根据曲线的曲率特性稀疏分布测点的位置,提高了测量效率和质量。针对现有自适应测量方法在测量过程中存在的特征遗漏和人为干预等缺陷,本文提出基于CMM的双参数向自适应测量方法来全自动测量具有自由曲面特征实物,旨在利用密度小的具有代表性的测点来表达被测曲面的几何特征信息。
1 双参数向自适应测量原理

图1 曲面测量参数方向确定Fig. 1 Direction determination of the surface’smeasuring parameters
采用CMM测量自由曲面时,可根据“曲面→曲线→点”的思想将曲面转化为点集的测量,通过扫描截面与被测曲面的交线形成扫描线,如图1所示。假设扫描截面都平行于OYZ平面,定义沿扫描线方向为测量U参数向,垂直于扫描线方向为测量V参数向。手动测量曲面的一系列边界点后,连接边界点形成可测区域,由可测区域自动拓扑生成V向几条均匀分布的初始扫描线和每条扫描线上均匀分布的几个初始点,初始扫描线的条数和每条扫描线上初始点的个数分别由U、V方向测量阶次确定,具体数值为“阶次值+1”。在确定V向均匀分布的初始扫描线和扫描线上U向初始均匀分布测点后,可指导CMM去全自动自适应测量整个曲面,这个过程又包含U向测点的自适应确定和V向扫描线跨距自适应确定。
1.1U向测点自适应确定
U向测点自适应确定方法为沿U向连续均匀初测k+1个点后,由这k+1个测点拟合一条k次非均匀B样条曲线。计算这条曲线末端处一、二阶导数得出曲线末端曲率,由此预测第k+2个测点位置和测量矢量,指导CMM测量该点,得到该点实测坐标后,重复上述过程,将测点重新拟合一条k次非均匀B样条曲线,然后计算曲率和测点。
同理,如图2所示,当CMM测量n+1个点后,拟合n+1个测点为曲线来预测下一测点位置,如果预测点的理论坐标值超出可测区域边界,就测量边界上的点,然后结束该条扫描线测量,转测下条扫描线,具体流程如图3所示。

图2 拟合n+1个测点为非均匀B样条曲线Fig.2 n+1 measured points are fitted to a non-uniformB-spline curve

图3 U向测点自适应确定Fig.3 Adaptive determination of measuring pointsin U direction
1.2V向扫描线跨距自适应确定
为实现被测曲面扫描线能随着曲面V向曲率变化而自适应分布,本文提出一种“动态的测量—反求曲面—测量”方法,即在初始均匀测量q+1条扫描线后,对已测的扫描线点云反求一张k×q次非均匀B样条曲面。确定出曲面上的V向等参数线,如图4所示。然后根据等参数线的方程确定等参数线末端的曲率值,对比所有等参数线的末端曲率值找出最大的曲率值,同时认为这个最大曲率值可代表非均匀B样条曲面V向边界最大曲率,通过最大曲率值计算出下条待测扫描线的跨距,具体的流程如图5所示。

图4 V向等参数线Fig.4 Isoparametric line of V direction

图5 V向扫描线跨距自适应确定Fig.5 Adaptive determination of the scan line spacingin V direction
待测扫描线的跨距确定后,由U向测点自适应确定方法对这条扫描线进行自动CMM测量。当该条扫描线测量完毕后,再利用所有已测扫描线点云重新反求出一张非均匀B样条曲面,然后根据新的非均匀B样条曲面继续确定出要测的下一条扫描线的跨距。重复这一过程,直至被测自由曲面片测量完毕。
2 双参数向自适应测量算法实现
2.1 扫描线上测点计算
每条扫描线自适应测量之前需测量均匀分布的k+1个初始点集Ti,该初始点集由可测区域边界起点自动拓扑生成,具体的表达式如下:
Ti=(x+HLxi,y+HLyi,z)i=0,1,…,n
(1)
式中,H为常数;x、y、z为扫描线边界起始点的坐标值;Lx、Ly为扫描线在X、Y轴方向的分量。
由于被测曲面的数学模型未知,无法得到初始点集的测量矢量,所以在初始点集的测量过程中只能事先人为地定义一个测量矢量,但这并不准确。然而测量矢量正确与否会影响测量结果精度,因此需在初测的基础上再进行精测以提高初始点集精度,具体步骤如下:①CMM初测k+1个初始点;②利用k次非均匀B样条曲线拟合这几个初始点;③计算每个初始点处的切矢量;④垂直于切矢量方向为测量矢量方向,计算每一点处的测量矢量;⑤根据每个初始点坐标值和测量矢量进行CMM测量获得初始点集的精测值。
拟合n+1个测点为k次非均匀B样条曲线[9-10]:
(2)
其中,di为曲线的控制顶点;Ni,k(u)为k次B样条基函数:
(3)
非均匀B样条曲线求导通式为
(4)
(5)
当参数u=1时,该测点即为曲线的末端点,曲线末端点的曲率kρ可由该点处的一阶导数和二阶导数求得,即
(6)
曲率半径ρ为
(7)

图6 扫描线跨距自适应确定原理图Fig.6 The principle of adaptive determination of thescan line spacing
对曲线末端进行圆弧延伸,如图6所示,圆弧AB即为延伸曲线段。A点表示为B样条曲线的终点,ρ为A点处的曲率半径,θ为跨度角,OA方向垂直于A点处的切线方向,e为测量过程中定义的测量精度阈值,AB间的弦长为预测点步长,B点即为预测点,测量矢量为BO方向。圆弧AB与弦AB的最大距离为CD,根据弦高法的原理[11],当所有点到弦AB上的距离都不超过阈值e时,则认为圆弧AB可以利用弦AB表示:
(8)

θ≤2arccos(1-ekρ)
(9)
当θ=arccos(1-ekρ)时,延伸线上的点到弦AB的距离为最大值e。根据式(9)可知,曲率kρ越小时,θ值就越小,AB之间的距离就越大,预测点的步长越大,反之则相反。预测点的步长s可表示为
(10)
为研究被测扫描线端点处曲率kρ对预测点步长的影响,假设阈值e=0.1 mm,如图7所示,预测点的步长会随着非均匀B样条曲线末端点处的曲率增大而减小。
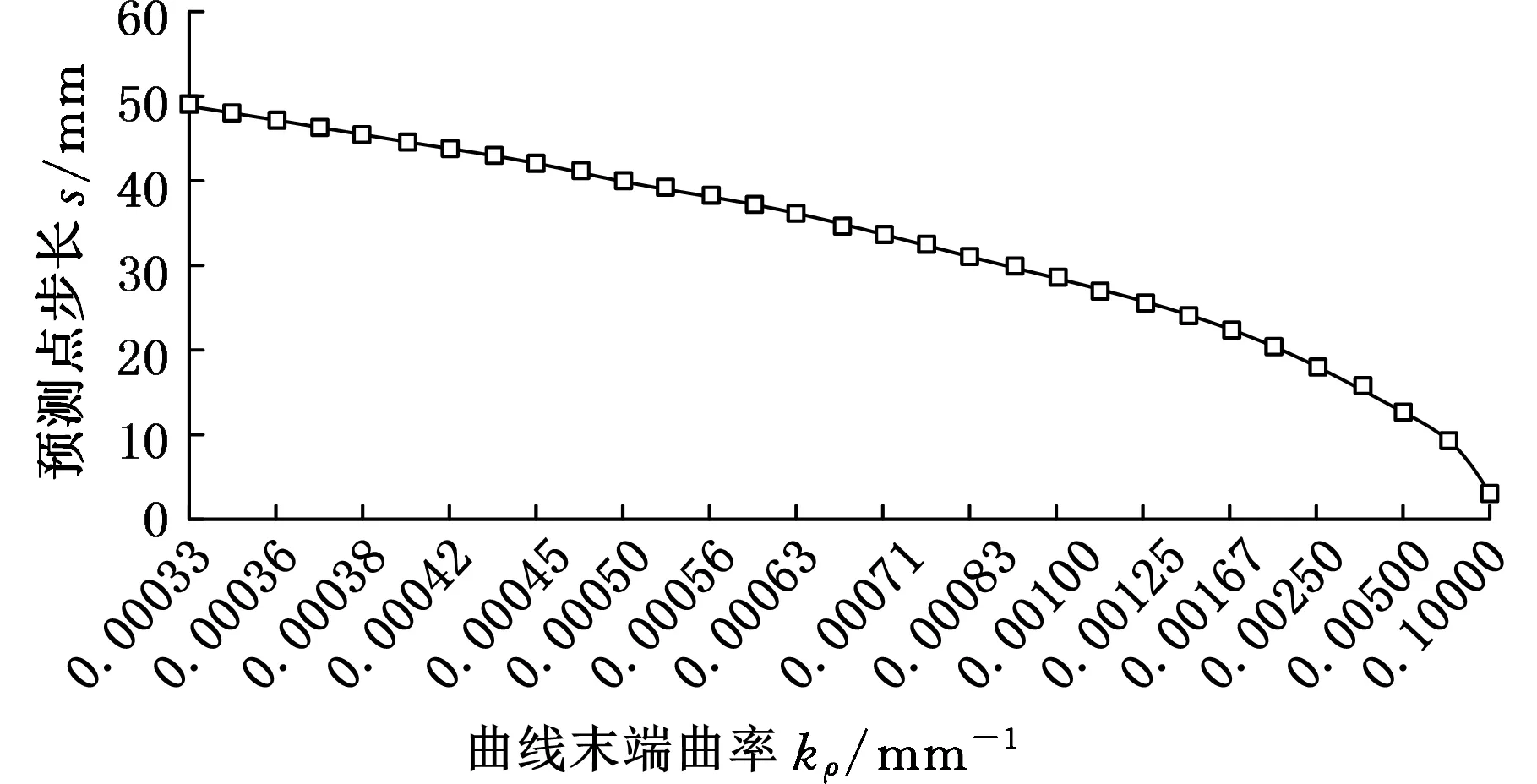
图7 预测点步长与曲线末端曲率的关系Fig.7 The relationship between the step length ofpredicted point and the curvature of terminal curve
不同测量精度阈值e对预测点步长会有不同的影响,取端点处的曲率kρ=0.01 mm-1,预测点步长随测量精度阈值e的变化关系如图8所示,其步长会随着精度阈值e的增大而增大。

图8 预测点步长与测量精度阈值的关系Fig.8 The relationship between the step length of predicted point and the measuring precision threshold
测点个数与预测点步长的关系如图9所示,预测点的步长越大,扫描线上的测点个数就越少,步长越小则测点个数越多。因此当被测扫描线的曲率越大即变化越剧烈时,预测点的步长越小,测点数目越多;被测扫描线的曲率越小即变化越平缓时,预测点的步长越大,测点数目越少;测点会随着被测扫描线曲率变化而疏密分布。

图9 测点个数与预测点步长的关系Fig.9 The relationship between the number ofmeasuring points and the step length of predicted point
2.2 扫描线间跨距计算
假设测量过程中对已测扫描线点云反求得到的非均匀B样条曲面为S(u,v)[12-13]:
(11)
式中,di,j为曲面的控制顶点集;k、q为曲面两个参数方向次数,Ni,k(u)、Nj,q(v)为k次和q次的B样条基函数。
则固定曲面上某一参数方向上的参数值,非均匀B样条曲面就会转化为曲面上一条等参数曲线[14]。例如固定参数u=u0,曲面S(u,v)则转化为关于参数v的等参数曲线Cu0(v):
(12)
等参数线Cu0(v)关于参数v的f阶导数可表示为
(13)

(14)
固定曲面不同的参数u值即可得到曲面上不同的等参数曲线Cu(v)。计算每条等参数曲线末端处的曲率值kρ(u),找出所有曲率值kρ(u)中的最大曲率值kρ(u),max。本文认为待测扫描线的跨距应根据最大曲率值kρ(u),max来确定,类似于U参数向,当kρ(u),max值越大时,则被测曲面沿V向的变化越剧烈,待测扫描线的跨距应该越小,则采集的数据不会遗漏曲面的重要特征,能更好地代表被测曲面,有利于后续逆向工程中模型反求。对应于最大曲率值kρ(u),max的曲率半径ρmin为
(15)
类似于预测点步长的确定方法,也采用弦高法确定出待测扫描线的跨距:
(16)
其中,e为测量精度阈值,与U参数向的阈值为同一数值,θ为跨度角,则待测扫描线的跨距L可根据V向最大曲率kρ(u),max确定:
(17)
3 实例应用
3.1U、V方向测量阶次对结果的影响
为研究U向测量阶次对测量结果的影响,以二、三、四、五次曲线分别作为测量对象进行模拟U向自适应测量。二次被测曲线为y=(x2+x)/50,三次被测曲线为y=(x3+x2+x)/4000,四次被测曲线为y=(x4+x3+x2+x)/(8×105),五次被测曲线为y=(x5+x4+x3+x2+x)/108,其中x∈[0,100]。U向阶次分别为3~8,即测量过程中非均匀B样条曲线的拟合次数分别为3~8次,预测误差统计结果如表1~表4所示。从表1~表4可以明显地看出预测精度已达微米级,且次数越高预测误差越小,测点个数越多。但实际测量过程中并不是次数越多越好,因零件表面粗糙度等不光滑原因,次数越多算法的振荡性越强,预测精度反而下降。

表1 二次被测曲线上不同U向测量阶次预测误差

表2 三次被测曲线上不同U向测量阶次预测误差

表3 四次被测曲线上不同U向测量阶次预测误差
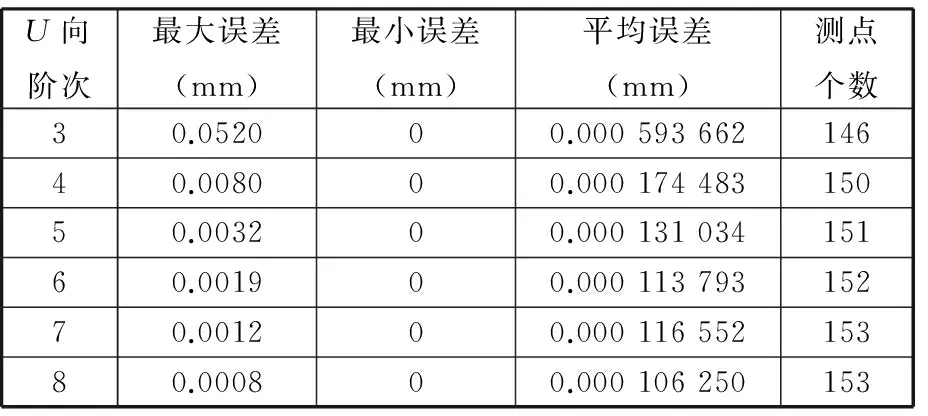
表4 五次被测曲线上不同U向测量阶次预测误差
探索V参数向不同测量阶次即测量过程中反求的非均匀B样条曲面V向阶次对测点分布结果的影响,以已知方程的理论曲面马鞍面作为测量对象进行模拟双参数向自适应测量,其方程如下:
(18)
x∈[0,30]y∈[0,43.66]
模拟测量过程中因主要研究V向测量阶次对测量结果的影响,故U参数向统一取5次,而V参数向分别取3~8次。测点的统计分析结果如表5所示,可以看出V向次数越高,扫描线的条数越多,扫描线间距越小,测点个数越多。
3.2 具有自由曲面特征自适应测量
对图10所示的具有复合自由曲面特征零件的第4个自由面片,分别采用扫描线跨距均匀分布和扫描线跨距自适应分布两种方式进行CMM测量,均匀跨距分别取2.1024 mm、3.7356 mm和5.3689 mm,其中2.1024 mm是跨距自适应测量中的最小跨距,5.3689 mm为最大跨距,3.7356 mm为最小跨距和最大跨距的平均值。测得的数据点云分别如图11~图14所示,统计结果如表6所示。

表5 不同V向测量阶次对测量结果的影响

图10 具有复合自由曲面特征零件Fig.10 Blade part with free-form surface features

图11 均匀跨距2.1024 mm测量点云Fig.11 Point cloud of uniform spacing 2.1024 mm

图12 均匀跨距3.7356 mm测量点云Fig.12 Point cloud of uniform spacing 3.7356 mm

图13 均匀跨距5.3689 mm测量点云Fig.13 Point cloud of uniform spacing 5.3689 mm

图14 自适应跨距测量点云Fig.14 Point cloud of adaptive spacing
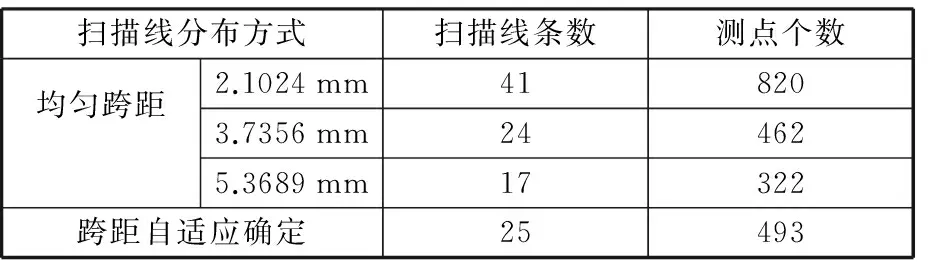
扫描线分布方式扫描线条数测点个数均匀跨距2.1024mm418203.7356mm244625.3689mm17322跨距自适应确定25493
对四种点云数据进行曲面重构精度评价,结果如图15~图18所示,统计结果如表7所示。

图15 均匀跨距2.1024 mm下测量点云曲面重构误差Fig.15 Surface reconstruction error of uniformspacing 2.1024 mm

图16 均匀跨距3.7356 mm下测量点云曲面重构误差Fig.16 Surface reconstruction error of uniformspacing 3.7356 mm

图17 均匀跨距5.3689 mm下测量点云曲面重构误差Fig.17 Surface reconstruction error of uniformspacing 5.3689 mm

图18 自适应跨距测量点云曲面重构误差Fig.18 Surface reconstruction error of of adaptive spacing

扫描线分布方式最大正向误差值(mm)最大负向误差值(mm)正向平均误差值(mm)负向平均误差值(mm)均匀跨距2.1024mm0.11301780.1204950.04271730.0476723.7356mm0.21438450.2344310.07093880.0774205.3689mm0.35710040.3278750.17634550.149680自适应跨距0.12787730.1172840.06196810.059494
根据表6和表7的结果对比可知,自适应跨距的测量数据和最小跨距的测量数据重构的曲面模型误差相近,但自适应跨距的扫描线相比最小跨距的扫描线减少了16条,减少百分比约为39%,测点数目减少了327个,减少百分比约为39.87%;对比于平均跨距,测点数目增加了6.28%,但曲面模型的精度提高了3倍以上;相对于最大均匀跨距,测点数目增加了34.68%,但曲面模型精度提高了一个数量级。
4 结语
手动测量被测曲面的边界点后,形成可测区域,在此基础上可实现全自动CMM自适应测量,得到结果测点文件,避免了测量过程中人为因素的干扰。测点可随被测曲面自身曲率变化特性而自适应分布,在曲率变化大的重要区域分布密集,曲率变化小的非重要区域分布稀疏,既保留了重要特征点又避免了数据冗余。自适应测量阶次越高,则测点密度越大,预测精度越高。对具有自由曲面特征的叶片等零件进行实际测量,结果表明本文方法测量精度可达微米级。
[1] AL-AHMARI A, AALAM J. Optimizing Parameters of Freeform Surface Reconstruction Using CMM [J]. Measurement, 2015,64:17-28.
[2] IAN M. The Evolution of CMM Probing Systems[J]. Manufacturers’ Monthly, 2014,1:20-21.
[3] GAPINSKI B, WIECZOROWSKI M, MARCINIAK-PODSADNA L, et al. Comparison of Different Method of Measurement Geometry Using CMM, Optical Scanner and Computed Tomography 3D[J]. Procedia Engineering, 2014,69:255-262.
[4] LI S Z. Adaptive Sampling and Mesh Generation[J]. Computer-Aided Design, 2005,27(3):235-240.
[5] KIM S W, SONG C K. Reverse Engineering: Autonomous Digitization of Free-formed Surfaces on a CNC Coordinate Measuring Machine[J]. International Journal of Machine Tools and Manufacture, 2007,37(7):1041-1451.
[6] ZHANG F Y, NEE A Y, FUH J Y, et al. A Neural Network Approach to Determining Optimal Inspection Sampling Size for CMM[J]. Computer Integrated Manufacturing System, 2011,9(3): 161-169.
[7] 何雪明, 李成刚, 胡于进,等. 三坐标测量机测量路径的曲率连续自适应规划[J]. 清华大学学报(自然科学版), 2007, 47(增刊2):1835-1839. HE Xueming, LI Chenggang, HU Yujin, et al. Continuous Curvature Adaptive Planning of the Measuring Path for CMM[J]. Journal of Tsinghua University(Science&Technology),2007,47(S2):1835-1839.
[8] 何雪明, 孔丽娟, 何俊飞,等. 基于三坐标测量机自适应测量的自由曲面逆向[J]. 机械工程学报, 2014, 50(15):155-159. HE Xueming, KONG Lijuan, HE Junfei, et al. Free-form Surface Reverse Based on CMM Self-adapting Measurement[J]. Journal of Mechanical Engineering, 2014,50(15):155-159.
[10] DENG Chongyang, LIN Hongwei. Progressive and Iterative Approximation for Least Squares B-spline Curve and Surface Fitting[J]. Computer-Aided Design, 2014,47:32-44.
[11] ROMAKINA L N. The Chord Length of a Hypercycle in a Hyperbolic Plane of Positive Curvature[J]. Siberian Mathematical Journal, 2013,54(5):894-904.
[12] ZHAO Xiuyang, ZHANG Caiming, XU Li, et al. IGA-based Point Cloud Fitting Using B-spline Surfaces for Reverse Engineering[J]. Information Sciences, 2013,245:276-289.
[13] AMBA D B, ARCHAK G, UJJAVAL G, et al. Reconstruction of Branched Surfaces: Experiments with Disjoint B-spline Surface[J]. Computer-Aided Design and Applications, 2015,12(1):76-85.
[14] PéREZ F, CLEMENTE J A. Constrained Design of Simple Ship Hulls with B-spline Surfaces[J]. Computer-Aided Design, 2011,43(12):1829-1840.
(编辑 王艳丽)
Adaptive Measurement of Free-form Surfaces Based on CMM Double Parameter Directions
HE Xueming1LI Yongping1WU Meiping1ZHANG Rong2
1.Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology,Wuxi,Jiangsu,214122 2.School of Science, Jiangnan University,Wuxi,Jiangsu,214122
A kind of adaptive measuring method for free-form surfaces was put forward based on double parameter directions of CMM. At first, a measurable area was generated by boundary points of the surfaces. Then, a few uniform initial scan lines and uniform initial measuring points of each line topology were automatically generated by the measurable area. A B-spline curves were generated by fitting the initial points that automatically measured by the CMM in theUparameter direction and the locations of next point were adaptively predicted by the end curve curvatures. A B-spline surface was fitted by the initial scan line’s point cloud, then the next line positions were adaptively determined by the border maximum curvatures of the surfaces in theVparameter direction, and the scanning lines ofUparameter direction were measured adaptively, until measurements were completed. Distribution density of the measuring points was determined by the curvature variation characteristics of the measured surfaces. The larger the curvature of the surfaces, the greater the distribution density of the measuring points and the smaller the curvatures of the surfaces, the smaller the distribution density of the measuring points, which guarantees the important feature points not leaking and avoid the data redundancy. The results of measurement experiments for theoretical curves and surfaces show that the measurement precision may reach μm level. The feasibility of the method was verified by an example of a part measurements.
free-form surface; coordinate measuring machine(CMM); double parameter direction; adaptive measurement; fully automation
2016-02-23
国家自然科学基金资助项目(51275210,51105175);江苏省产学研项目(BY2013015-30);江苏省六大人才高峰项目(2013-ZBZZ-016);中央高校基本科研业务费专项资金资助项目(JUSRP51511)
TP301
10.3969/j.issn.1004-132X.2017.05.004
何雪明,男,1966年生。江南大学江苏省食品先进制造装备技术重点实验室教授、博士。E-mail:hxuem2003@163.com。主要研究方向为自由曲线曲面CAD/CAE/CAM和逆向工程。李咏平,男,1991 年生。江南大学机械工程学院硕士研究生。武美萍,女,1970年生。江南大学机械工程学院副院长、教授、博士研究生导师。张 荣,女,1962年生。江南大学理学院副教授。
