基于小生境遗传优化算法的配电网无功优化

，，，，

(1.国网沈阳供电公司，辽宁 沈阳 110021；2.国网吉林省电力有限公司电力科学研究院，吉林 长春 130021;3.国网辽宁省电力有限公司营口供电公司，辽宁 营口 115000)

1 引言

配电网无功优化不但可以有效降低系统网损,对于提高系统电压合格率同样作用显著,进而降低网络运行费用,提高供电质量[1]。配电网潮流计算作为配电系统无功优化的基础和工具，其计算速度和收敛性将对优化效果产生直接影响。因此，根据无功优化的特点对潮流算法进行改进将有助于节能降损[2]。国内外学者对此做了大量的研究与报道。文献[3]建立有功网损最小的无功优化数学模型，利用改进的遗传算法进行问题求解，有效提高了收敛速度。文献[4]建立计及系统网络损耗和电压偏移的多目标无功优化数学模型，利用多目标智能优化算法求解模型，有效解决各目标函数之间的内在联系。文献[5]建立有功损耗最小的无功优化模型，提出一种改进的量子差分算法求解无功优化问题，采用并行处理技术有效降低算法寻优过程局部早熟的概率。以上文献主要从优化算法的角度求解无功优化问题，有效改善了寻优过程的全局收敛性能，但忽视了系统潮流运行方式对配电网无功运行的影响。

另一方面，配电网潮流计算方式主要包括：前推回代法、牛顿法和直接法三种形式[6]。文献[7]建立三相支路形式的配电网无功优化数学模型，利用混合整数二阶锥算法求解问题，能有效处理离散型电容器组的优化问题。文献[8]考虑辐射状配电网运行方式，建立基于回路导纳矩阵的支路追加法，有效处理了被追加支路与原网络中的部分支路存在耦合的情况。

针对以上问题，本文首先提出一种改进的支路追加法，以提高潮流计算过程中的收敛性，并将其用于电力系统无功优化问题上。其次，建立考虑系统网络损耗的电容器组配电网无功优化数学模型，针对传统遗传算法在处理高维复杂变量优化问题上的缺陷，结合小生境技术的优势，提出一种改进的小生境遗传优化算法求解无功优化模型。最后，以IEEE-33节点测试系统为例，验证本文方法的高效性。

2 支路追加潮流计算方法

支路追加法的基本思想是，给定节点电压初值，把节点负荷复功率等效为一个与“地”相连的复阻抗支路，取根节点至负荷节点所有支路作为一个回路。建立针对所有负荷节点的回路电压电流方程为：

ZLPILP=ULP

(1)

式中：ZLP为回路阻抗矩阵；ULP为各回路电压源构成的列向量；ILP各回路电流构成的列向量。

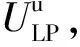
(2)

式中：AT为节点-树支支路关联矩阵；AL为节点连支关联矩阵；AS为根节点-树支支路关联矩阵；Uroot为根节点电压。

3 电力系统无功优化数学模型

配电网中的无功优化指在满足设备和系统运行约束条件下，通过调节有载调压变压器的分接头、以及无功调节电容器的投切组数来改变系统的潮流分布，实现维持电网安全、稳定、经济运行，保证供电质量的目的，其实质是一个多维的非线性规划、寻目标函数最优的数学问题。基于有功网络损耗最小的目标函数为：

(3)

式中：Ui，Uj为节点i，j的电压幅值；Gij，Bij，θij为节点ij之间的电导、电纳及电压相角；H为所有与节点直接相连的所有节点集合。

约束条件包括等式约束和不等式约束条件，分别为：

Pflow(x,u)=0

(4)

(5)

4 小生境遗传算法在无功优化中的应用

4.1 小生境遗传算法简介

遗传算法是模拟生物界进化过程方法，在1969年由J.Holland教授提出后经由De Jong.Goldberg等人在1975年归纳总结出来。与其他智能算法相比对于一些大型的、非线性多变量的复杂的数学问题，遗传算法更能显示出比传统的数学算法更加独特的优越性能[9]。但是，传统的遗传算法存在搜索全局最优能力不强、易早熟收敛的缺陷，从而不能得到全局最优解。因此，本文将小生境技术[10]与遗传算法相结合，由于小生境技术可以保持整个种群的多样性，将那些染色体中遗传基因较为相似的个体聚集成小种群，并将它们分到适应度函数图像中“峰值”上，然后再通过遗传算法对这些“峰值”进行处理，结果是使得适应较高的个体继续可以保持或者增加其适应度值，而适应度较低的个体其适应度值将大幅度降低而被淘汰，这样既可以保证个体可以分散在全局范围中扩大了搜索范围，也可避免整个函数陷入局部最优。

4.2 小生境遗传算法无功优化实现步骤

小生境遗传算法在无功优化过程中的具体步骤为：

(1)初始化种群个体：以各节点所接入电容器组数作为控制变量，由于电容器的组数为固定整数，采用十进制整数编码，具体情况表示为：

X=[x1,x2,…xi…xNC]

选取2011年1月—2015年12月于安徽医科大学附属第四医院诊治的晚期胃癌患者100例，男性46例，女性54例。对照组患者给予多西他赛联合顺铂、氟尿嘧啶静脉治疗，试验组患者给予多西他赛联合顺铂、氟尿嘧啶腹腔灌注，两组患者在年龄、性别及病灶部位上相比，差异无统计学意义，见表1。

(6)

式中：xi为节点i所投运电容器的组数；NC为安装电容器的节点数。

(2)适应度函数计算：遗传算法中的适应度值是群体进化的依据，个体进化到下一代的记录根据其适应度值来判断。适应度函数越大的个体越优良，则应赋予其较强的遗传能力，保证其优良特性可以很好繁衍；适应度函数越小的个体，则应对其变异使之进步，后面会继续对此进行说明。目标函数以网损值最小为最优。故而本文采取：

fit(f(X))=1/f(X)

(7)

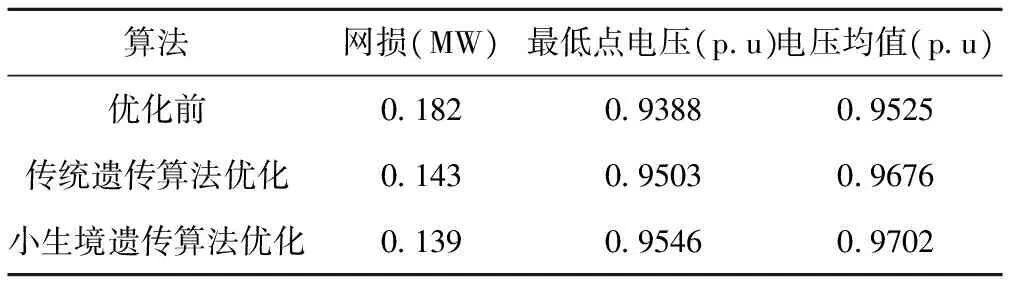
(3)遗传操作首先随机选出个M个体，设置计数器时间t=1。然后计算选出的每个个体对应的适应度值，最后将个体适应度值进行降序排列，其次，从中提取出N(N

(8)

式中：i=1,2,…,M+N-1；j=i+1,…,M+N。

当海明距离小于小生境半径d时，将Xi和Xj的适应度值进行比较，惩罚适应度较低的个体，降低其适应度值，从而不仅可以大大减少其遗传到下一代的概率，可以保留优良的个体，还使得在海明距离d内将只存在一个适应度优良的个体，既可以使个体之间保持一定的距离又能够有效保持种群多样化。

将进行小生境操作后的M+N个个体按新的适应度进行降序排列，分别记忆前N及M个个体。设定一个最大遗传代数T，如果tT，则认为没有其他最优解代替这个最优值，算法终止。

5 算例分析

在IEEE33节点配电系统6、15、29、31四个节点接入投切电容器，四个电容器的可投切范围均为150KVAR×7，系统结构图如图1所示，其对应的功率基准容量为10MVA，电压基准值为12.66kV。设置算法交叉率和变异率分别为0.8和0.1。最大迭代数T为80。

图1 IEEE-33节点配电系统

基于传统遗传算法，采用支路追加法进行无功优化中目标函数的计算时，获得的电容器容量比较结果如表1所示。

表1 传统遗传算法下无功优化方案

基于小生境遗传算法，采用支路追加法进行无功优化中目标函数的计算时，获得的电容器容量比较结果如表2所示。

表2 小生境遗传算法下无功优化方案

表3是采用不同优化方案时进行无功优化前后系统网损和节点电压情况的比较，系统节点电压幅值由图2所示。

表3 不同算法下网损和节点电压的比较

优化结果表明，由于电容器提供的无功补偿，系统各节点电压提升显著，降损同样明显。采用传统遗传算法进行无功补偿后，最低点电压从0.9388p.u提升到了0.9503p.u.，而采用改进后的遗传算法进行无功补偿后，最低点电压则达到0.9546p.u.；两种方法系统网损减少明显，其中采用传统遗传算法的无功补偿后，网损由优化前的0.182MVA降低到0.143MVA，而采用小生境遗传算法的无功补偿后，网损则达到0.139MVA。两种算法都使得目标函数下降明显，提高了系统的运行特性，但相比之下，改进的小生境遗传算法效果更为显著。从图2可以看出，采用两种优化算法都可以使电压合格率达到100%。

图2 无功优化前后各节点电压情况

6 结论

本文以实现系统网络损耗最小为目标建立了目标函数，利用改进后的支路追加法潮流计算采用节点对地等效负荷修正量计算潮流的特点，把各节点安装电容的投运容量值并入对地等效负荷中，将其用于配电网无功优化中适应度的计算。对遗传算法的特性进行分析，采用改进小生境的遗传算法。小生境遗传法可以在遗传算法原有的优势基础上，弥补遗传算法中的易早熟这一缺点，对所有的约束条件进行了处理，极大的增强了算法在全空间范围内搜索最好解的能力，很好地处理无功优化中连续变量和离散变量，有效地求解无功优化问题。

[1] 崔挺，孙元章，徐箭，等.基于改进小生境遗传算法的电力系统无功优化[J].中国电机工程学报，2011，31(19)：43-50.

[2] 闫丽梅，谢明霞，徐建军，等.含分布式电源的配电网潮流改进算法[J].电力系统保护与控制，2013，41(5)：17-22.

[3] 赵坤，耿光飞.基于改进遗传算法的配电网无功优化[J].电力系统保护与控制，2011，39(5)：57-63.

[4] 李鸿鑫，李银红，李智欢.多目标进化算法求解无功优化问题的比较与评估[J].电网技术，2013，37(6)：1651-1658.

[5] 马玲，于青，刘刚，等.基于量子差分进化算法的电力系统无功优化[J].电力系统保护与控制，2013，41(17)：39-43.

[6] 王建勋，吕群芳，刘会金，等.含分布式电源的配电网潮流快速直接算法[J].电力自动化设备，2011，31(2)：17-21.

[7] 刘一兵，吴文传，张伯明，等.基于混合整数二阶锥规划的三相有源配电网无功优化[J].电力系统自动化，2014，38(15)：58-64.

[8] E.K.Stanek.Algorithm for formation of loop admittance matrix[J].IEEE Transactions on Power Apparatus and Systems,1972,91(5):1743-1749.

[9] G Boone,H D Chiang.Optimal capacitor placement in distribution systems by genetic algorithm[J].International Journal of Electrical Power and Energy Systems,1993,15(3):155-162.

[10] 李惠玲，盛万兴，张学仁，等.改进小生境遗传算法在电力系统无功优化中的应用[J].电网技术，2008，32(17)：29-34.