一种改进的类功率下垂控制研究

，,，，

(广西大学电气工程学院，广西 南宁 530004)

1 引言

当前，能源需求趋紧，以保护环境为前提的可持续发展理念受到广泛重视。国际上对分布式发电领域给予了更多的期待。作为分布式电源大规模应用的有效技术实现途径，微网技术可通过柔性控制降低分布式能源并网对大电网的影响，实现能源的高效利用。而微网中的部分微源如光伏、蓄电池等均以逆变器为媒介，实现与微网相连。因此，实现微网逆变器的并联运行下垂控制的研究具有十分重要的现实意义[1-3]。

传统的下垂控制的思想在于，利用本地信息计算有功功率和无功功率，根据下垂特性曲线，调整微源接口的逆变器的输出电压和频率[4]。为实现均流，则需通过测量公共耦合点处电压参与下垂控制。但是，传统的下垂控制缺乏对具体线路阻抗特性的考量，其假设前提为输电线路为感性的架空线路，对于存在阻性或者阻感性的输电线路的微网不适用。文献[5]提出采用旋转坐标，通过坐标变换，从而避免线路阻抗对于功率的耦合作用。但是，公共耦合点处的电压反馈信号的传输增加了通讯成本，传输距离和信号传输准确性也成为必须考虑的问题。文献[6]提出了类功率的概念，但是仅停留在所有微源均采用完全相同的线路，也未对微源容量不同对于分配的影响加入考虑。因此，本文提出一种改进的的类功率下垂控制策略，仅根据本地信息，以微源单元输出量为观测量，通过类功率的形式，实现控制量的解耦，完成不同容量微源单元的功率分配。

本文通过分析并联微源模型，提出类功率下垂控制方法，实现控制量的解耦和负荷功率的精确分配。通过仿真分析，证明了类功率下垂控制策略的可行性和优越性。

2 微源并联系统功率分配分析

考虑如图1所示两个微源并联模型，进行并联系统分析。微源单元为分布式电源通过逆变器接口经过滤波单元的等效交流源。

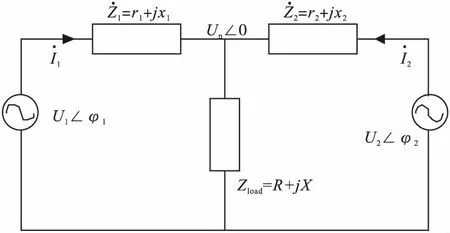
图1 微源并联系统模型

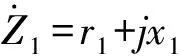
本文中计算仅根据可测的本地信息，利用KCL定律，有：

(1)

公共耦合点电压可表示为：

(2)

那么，可求得微源1输出电流为：

(3)

本文在计算输出复功率时可采用微源单元输出电压即本地电压，而非公共耦合点电压，求得微源1输出复功率为：

(4)

为了表示方便后文描述，令：

(5)

将式(5)带入式(4)，微源1发出的复功率简化为：

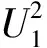
(6)

即，微源1发出的有功与无功功率为：

(7)

同理，可得微源2发出的有功与无功功率为：

(8)

由式(7)与式(8)，微源发出的有功与无功功率均与U1、U2、φ1、φ2相关。而传统的下垂控制把线路视为感性，即x>>r时，认为相位角由有功功率决定，电压由无功功率决定，忽略了有功功率与电压的关系、无功功率与相位角的关系。当微源所在为低压微网时，即线路为阻性或阻感性，那么有功功率与电压的关系、无功功率与相位角的关系不能被忽略。

因此，有功功率与电压的关系、无功功率与相位角的关系应该考虑入下垂控制的控制律设计中。那么，是否能寻求某两个变量，通过相关变形，使得这两个变量仅仅与电压或者是相位角有关，从而实现控制量的解耦呢？因此，本文利用“类功率”的概念，仅利用本地信息，根据有功功率与无功功率的线性组合，寻找 “类有功功率”P1t、P2t，使其差值仅与相位角有关的；寻找“类无功功率”Q1t、Q2t，使其差值仅与电压差有关的。

除了控制量解耦与通讯成本，在下垂控制设计中，各微源对负荷功率的分配也是探究要点之一。在不同容量微源并联的微网中，环流大小是衡量系统功率分配的重要指标。如果能按照额定容量比k精确分配负荷功率，精确设定电压和频率参考点，则并联微源能够稳定运行，同时抑制环流。那么，“类功率”实现控制量解耦的同时，是否能实现微源出力对应容量成比例满足负荷功率需要呢？如果微源发出的类有功功率和类无功功率对应成比例，是否真正的输出有功功率与无功功率也能满足精确的负荷功率分配呢？本文将在随后解答这个问题。

3 类功率下垂控制

由前文可知，类功率为有功功率与无功功率的线性组合，即：

(9)

假设微源1、2容量比为k。如果两微源按照容量之比发出类有功功率和类无功功率，则有：

P1t-kP2t=(k11P1+k12Q1)-k(k21P2+k22Q2)=

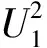
(10)

Q1t-kQ2t=(k13P1+k14Q1)-k(k23P2+k24Q2)=

k14c+kk23b+kk24c)+U1U2cos(φ1-

φ2)(k13c-k14b-kk23c+kk24b)

(11)

若要求微源的类有功功率功率仅与相角相关，那么经调节使得相角差为0时，微源1、2须根据容量比精确分配负荷的类有功功率功率。而要求微源的类无功功率仅与电压差相关，那么经调节使得电压满足对应关系时，微源1、2须根据容量比精确分配负荷的类无功功率功率。则式(10)与式(11)的相关参数须满足：

(12)

即类功率参数的选择须满足式(12)；同时，等效输出阻抗满足r2/r1=x2/x1=k时，类功率按照微源容量等比例分配。

所以，有：

(13)

此时类有功功率的差值仅与相角差有关，类无功功率的差值仅仅与电压差有关：

(14)

由式(14)可知，如果有φ1>φ2，则必然推出P1t>kP2t；若U1>U2，则必然推出Q1t>kQ2t。因此，经过调节，系统会稳定在P1t=kP2t与Q1t=kQ2t。

那么，记U1=U2=U。此时微源1、2输出的有功功率和无功功率关系如下：

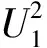
(15)

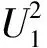
(16)

由于，此时有r2/r1=x2/x1=k，故有P1=kP2和Q1=kQ2。也就是说，当微源输出的类有功功率和类无功功率对应容量成比例时，它们输出的实际有功功率和无功功率也对应成比例，从而消除了环流，有利于系统的稳定运行。

根据上述推导，所选下垂控制方式为类下垂功率控制：

(17)

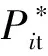
4 仿真分析

为验证控制策略的合理性，在MATLAB/SIMULINK平台中搭建仿真模型进行仿真实验。

以图1所示的两微源并联进行仿真。微源1与微源2容量比为1∶2。系统初始工况为2个微源分别带有功负荷20kW和40kW；在0.5s时，两微源并联；在1s时，公共耦合点新增有功负荷40kW和无功负荷24kVar。主要考察不同容量微源并联时，分别工作在传统功率下垂控制与类功率下垂控制下的微源是否按照容量比增发功率满足负荷需求，考察环流大小。Droop曲线为传统下垂控制；QuasiDroop曲线为类功率下垂控制。

从图2可以看出，对比传统的功率下垂控制律和类功率下垂控制律：在传统的下垂控制方法下基本可实现有功功率的按比例分配，原因在于系统稳定时两微源的频率会拉入同步。所以只要将设定下垂系统成比例，则可满足有功功率的按比例分配。但是由于存在电压偏差，无法满足无功功率的按比例分配。同时输出电流的幅值和相位差值无法忽略，即存在着明显的环流。而与之相比，在类功率下垂控制方法下，基本可以实现有功功率与无功功率的按照容量等比例下降，且输出电流的幅值和相位很小，环流较小，实现了较为精确的功率分配和环流抑制效果。

5 结论

本文根据不同容量微源并联系统特点，提出了一种改进的类功率下垂控制策略，消除控制量的耦合，实现不同容量微源对于负荷功率的精确分配。

首先分析了微源的并联模型。根据本地信息，推出微源的输出功率的表达式。引入“类功率”的概念，利用有功功率和无功功率的线性组合形式得出类有功功率和类无功功率，使得类有功功率仅与微源输出频率相关，类无功功仅仅与微源输出电压相关，实现了控制量的解耦。同时，实现负荷功率按照微源容量进行分配，完成功率的精确分配。最后以不同容量微源并联进行仿真实验。不同容量微源并联时，能够有效地减少系统环流，提高功率的分配精度。仿真实验证明，无互联线的类功率下垂控制策略在无需测量公共耦合点处电压的情况下，具有良好的负荷功率分配特性。

[1] LASSETER R.H.,PAIGI P.Microgrid:a conceptual solution[C].Power Electronics Specialists Conference,2004.PESC 04.2004 IEEE 35th Annual,2004:4285-4290.

[2] 王成山,王守相.分布式发电供能系统若干问题研究[J].电力系统自动化,2008,(20):1-4.

[3] CORNFORTH D.,MOORE T.,SAYEEF S.Challenges and opportunities for inverters in microgrids[C].IECON 2011-37th Annual Conference on IEEE Industrial Electronics Society,2011:3111-3116.

[4] 王成山,李琰,彭克.分布式电源并网逆变器典型控制方法综述[J].电力系统及其自动化学报,2012,(2):12-20.

[5] 周贤正,荣飞,吕志鹏,等.低压微电网采用坐标旋转的虚拟功率V/f下垂控制策略[J].电力系统自动化,2012,(2):47-51.

[6] 阚志忠,张纯江,薛海芬,等.微网中三相逆变器无互连线并联新型下垂控制策略[J].中国电机工程学报,2011,(33):68-74.