巧用判别式化解运算难度

福建省泉州市第七中学 (362000) 林志斌 郭富梅

巧用判别式化解运算难度

福建省泉州市第七中学 (362000) 林志斌 郭富梅

2017年高考考试大纲对运算能力的要求重点提到，会根据法则、公式进行正确的运算，能根据问题的条件寻找与设计合理、简捷的运算途径，会选择运算公式，确定运算程序等一系列过程中的思维能力．解析几何中直线与圆锥曲线的位置关系是考察运算能力的重要题型之一，主要是以含字母的式的运算为主，同时要兼顾运算，逻辑推理等能力的考察．在解题过程中，用到判别式的运算量大，学生在计算时极易出错，导致后面都失分．哪如何能快准的运算呢？本人在教学中依据书本教学内容，加以推广，发现了一个很好记忆的结论．使之在计算过程中准确率高，运算速度快，化解了运算难度．

一、探究直线与椭圆的位置关系

设直线方程为Ax+By+C=0，椭圆方程为

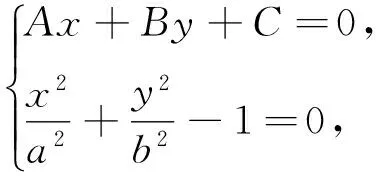
二、类比推广

2.1 直线与双曲线的位置关系

2.2 直线与中心在(x0,y0)的椭圆位置关系

联立直线与椭圆方程

2.3 直线与中心在(x0,y0)的双曲线位置关系

联立直线与双曲线方程

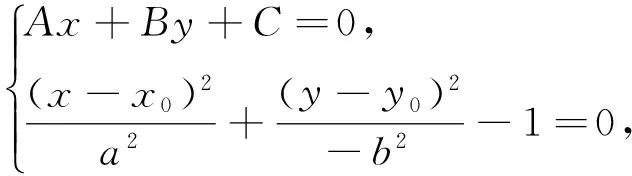
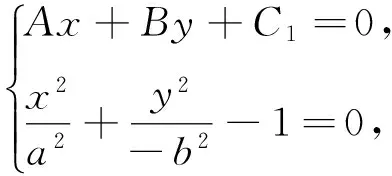
三、结论的应用

3.1 利用结论求参数的取值范围

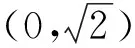
3.2 利用结论证明相切问题

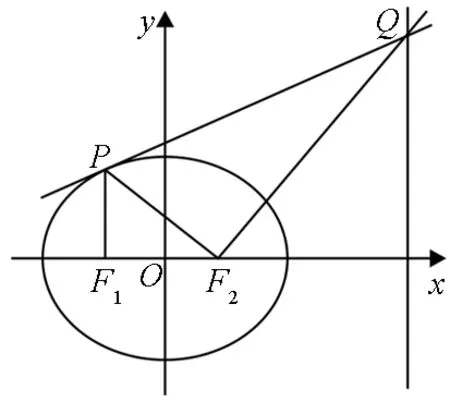
图1

3.3 利用结论求切点坐标

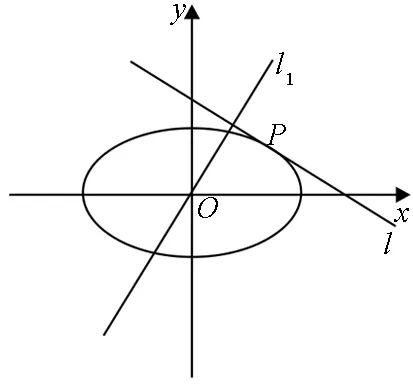
图2

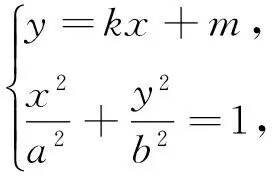
3.4 利用结论求最大值

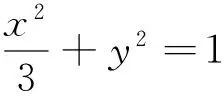
3.5 利用结论求与弦长有关问题

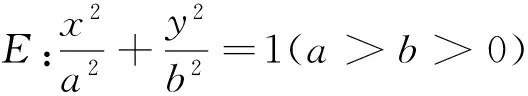
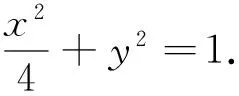
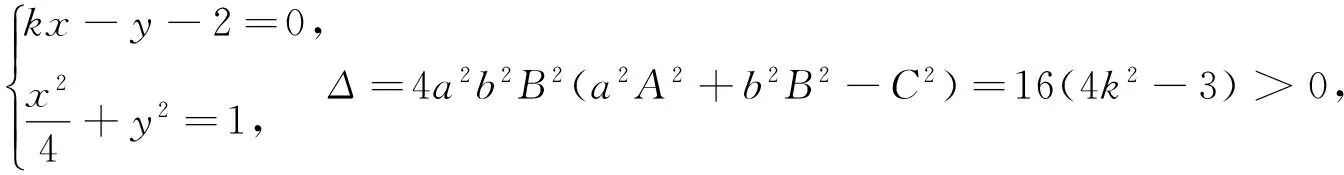
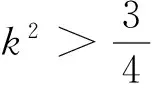
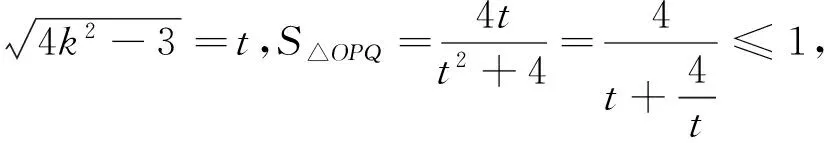
本人通过多年的教学实践发现，学生能容易记住结论，在计算过程中省略很多繁杂的运算，节约大量的时间，提高了准确率，使学生不再惧怕解析几何，并能得心应手的去解高考题，这样既以教材和大纲为依据，也体现解法无止境，真正体现大纲的精神．

[1]]杨尧伟．判断直线与椭圆的位置关系何需舍近求远[J]．中学数学教学参考，2014(1-2)：55.