例析矛盾分析法在多变量数学问题中的运用

西安交通大学苏州附属中学 (215028) 王丽利

例析矛盾分析法在多变量数学问题中的运用

西安交通大学苏州附属中学 (215028) 王丽利

马克思主义哲学原理告诉我们：矛盾存在于一切事物的发展过程中，一切事物都是运动的，在运动过程中存在着各种矛盾，它们的地位和作用又不尽相同，在矛盾系统中居于支配地位、对事物发展过程起决定作用的矛盾，我们称为主要矛盾，其它矛盾则称为次要矛盾.我们在综合把握事物的矛盾系统时，一方面要注意整个事物中诸多矛盾的协同发展，另一方面又要分清主次，着重抓主要矛盾，这样才能理清事物发展的主要线索.

矛盾分析法对数学解题具有重大的指导意义.在一个多变量数学问题中，我们选择一个变量作为主要变量，而将其余变量当作次要变量(或常数)，通过对主要矛盾的研究、分析，确定解题方向，这种方法我们称为主元法.

例1 (日本高考题)设不等式2x-1>m(x2-1)对满足|m|≤2的一切m的值成立，求x的范围.

分析:不等式mx2-2x+1-m<0中有两个变量x，m，受思维定势影响，我们习惯上把x作为主要变量，将不等式变形为mx2-2x+1-m<0，撇开不等式难解不说，即使解得x的范围，也必然与m有关，因此你的解题才走到中途点，还要继续考虑恒成立的条件，彻底摆脱变量m；如果由构造函数y=mx2-2x+1-m，但x的范围是解题目标，也就是说你无法预先确定定义域，因而你构造的是一座空中楼阁.

多次受挫，怎么办？以m为主要变量如何？

原不等式变形为m(x2-1)-(2x-1)<0,令f(m)=(x2-1)m-(2x-1)(-2≤m≤2).

因此以m为主要变量构造函数f(m)，情况大为改观了，此时函数f(m)的定义域确定了，有了稳固的大本营，解题可以畅通无阻地推进了.

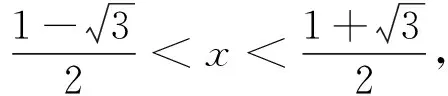
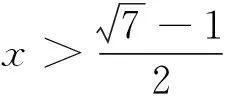
例2 (课后习题改编)x、y、z∈R,在△ABC中，求证：x2+y2+z2≥2xycosC+2zxcosB+2yzcosA.

分析:本题中有六个变量x、y、z与A、B、C，可谓复杂.我们选择x为主要变量，则原不等式整理为

x2-2(ycosC+zcosB)x+y2+z2-2yzcosA≥0.

抓住了主要矛盾，也就能驾驭事物的发展过程，因此只要验证上式的判别式△≤0.

△=4(ycosC+zcosB)2-4(y2+z2-2yzcosA)=4(-y2sin2C-z2sin2B+2yzcosBcosC+2yzcosA)=4[-y2sin2C-z2sin2B+2yzcosBcosC-2yzcos(B+C)]=4(-y2sin2C-z2sin2B+2yzsinBsinC)

=-4(ysinC-zsinB)2≤0.

评注:正是抓住了主要矛盾，一个复杂问题迎刃而解了.例2被称为三角形镶嵌不等式，通过取特殊值，我们可以成批地得到三角不等式.如：

例3 (全国竞赛题)求一切实数p，使三次方程5x3-5(p+1)x2+(71p-1)x+1=66p的三个根均为自然数.

分析:原方程变形为5x3-5(p+1)x2+(71p-1)x+1-66p=0.即5x2(x-1)-(x-1)-p(5x2-71x+66)=0,(x-1)(5x2-1)-p(x-1)(5x-66)=0,(x-1)(5x2-5px+66p-1)=0.

很多选手都是这样求解，实际上没有捕捉到主要矛盾，本题的焦点是：两根x1,x2均是自然数，因而x1,x2是优先于p的主要变量，通过对x1,x2的分析，才能更好地确定解题方向.

由②③消去p得5x1x2=66(x1+x2)-1,即(5x1)(5x2)=66(5x1+5x2)-5,(5x1-66)(5x2-66)=1×4351=19×229=(-1)×(-4351)=(-19)×(-229),故5x1-66与5x2-66是4351的约数，共可列出8个方程组，易得p=76，满足①，即存在唯一实数p=76，使原方程有三个自然数解.

在日常教学中,引导学生接触哲学,教会学生利用哲学的思想方法解决数学问题,这对于提高学生的学习效率、培养适应个人终身发展和社会发展需要的必备品格与关键能力都是很有好处的.培养学生的探究精神和数学素养，是在数学学习过程中逐步形成的，不能只流于形式和口号，而要扎扎实实地落实在教师的教学实践和学生学习的每一个环节、每一处细节之中.