一道模拟调研填空题的多视角求解

江苏省常州市田家炳高级中学 (213000) 徐 颖

一道模拟调研填空题的多视角求解

江苏省常州市田家炳高级中学 (213000) 徐 颖

美国著名数学教育家波利亚说过，掌握数学就意味着要善于解题.当遇到一个新问题，总想用熟悉的题型去“套”，这仅仅只是解出来，并没有真正意义上弄懂它，只有对数学思想方法理解透彻，会举一反三时，才能提出新看法、巧解法.近年数学高考十分重视对于数学思想方法的考查，尤其突出对能力的考查，其解答过程都蕴含着重要的数学思想方法.我们要有意识地应用数学思想方法去分析问题、解决问题.高中数学思想方法有很多，这里重点说说换元法.

换元法又称为“变量代换法、辅助元素法”.换元的实质是转化，关键是构造元和设元，理论依据是等价代换，目的是变换对象，将问题转化在新对象的知识背景下去研究， 把分散的条件联系起来，把隐含的条件显露出来，把条件和结论联系起来，把非标准问题标准化，复杂问题简单化，陌生问题熟悉化[1].本文将以南通等市的2016届高三调研卷上的一道填空题为例，浅谈几种换元法的妙用.

1.试题呈现

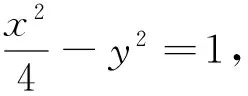
2.解法探究

2.1 目标换元法

处理最值时，通常将目标函数看作一个未知变元，通过它与已知条件建立等式或不等式.

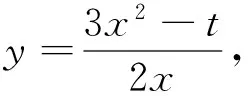
注意，当u=4时，8u2+(4-6t)u+t2=t2-24t+144=(t-12)2≥0,故只需要

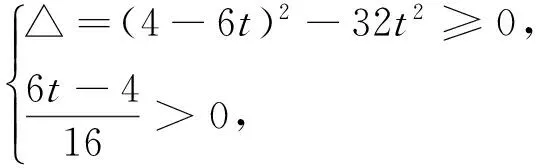
评注：本解法实际上经过了2次换元，第1次从目标函数入手，通过消元，建立t,x的新关系；第2次换元是降次，关于x的四次方程难以解决，于是考虑换元成熟悉的二次，但在此过程中，需要再次注意新元的范围，后面是一个二次方程有解问题，易错.开头的目标换元应该是学生比较容易想到的，在线性规划这块用得较多.虽然入手容易，但是后面较难解决.所以很多学生半途而废.

2.2 “1”的妙用

分析：注意到所求的表达式是二次齐次式，而题意条件给出也是齐次式，还是常数1，于是考虑用“1的代换”.

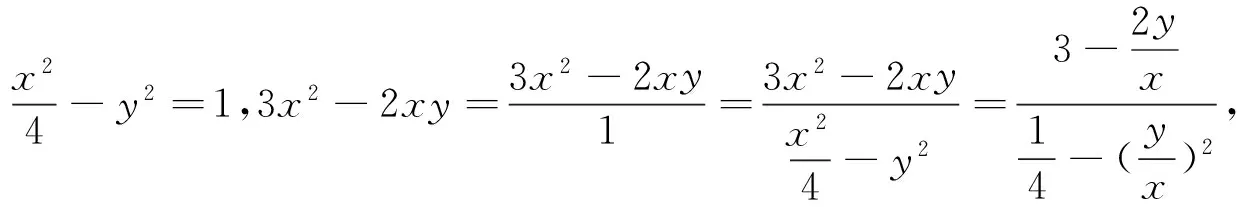
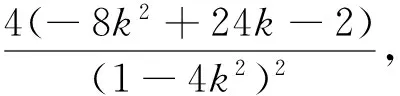
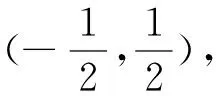
2.3 比值换元[2]

如果已知条件为比例式子或者可以看作比例，那么用比值代入可使其简化.本题给出的条件是二元齐次式，不妨引入参数k，考虑用正比例函数将两个变量的依存关系表示出来，从而使二元变量的最值问题转化成一元变量的最值.

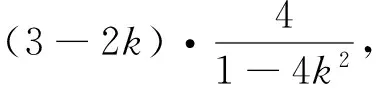
2.4 三角换元

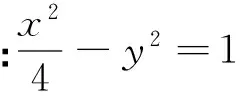
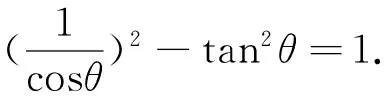
2.5 和差换元

若x,y∈R,则可设x=a+b,y=a-b,特别地，若x+y=2a,则可设x=a+t,y=a-t,(t∈R)，这样的换元我们称之为和差换元.

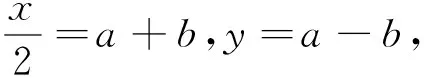
2.6 极坐标换元

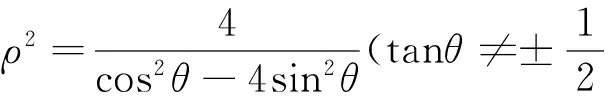
3x2-2xy=3(ρcosθ)2-2ρcosθ·ρsinθ

=ρ2(3cos2θ-2cosθ·sinθ)

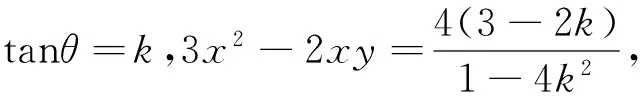
评注：转换视角，置于不同的坐标系，有创意！这个解法精妙之处在于题干和所求均为齐二次式，否则处理难度便会加大.极坐标变换是理科生学习的内容，所以这个解法对于文科生的学习能力要求较高.

2.7 局部换元

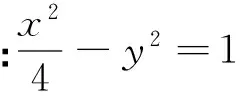
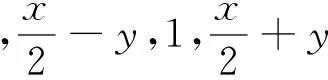
3.解题反思

至此，笔者给出了一道调研模拟题的7种换元解法.在分析问题时，需要关注条件及所求结论的特点和相互联系，从不同视角寻找问题的突破口. 我们使用换元法解题时要注意以下两点：(1)选择合适的变量进行换元，要遵循有利于运算、有利于标准化的原则；(2)换元后要注重新变量范围的选取，一定要使新变量范围对应于原变量的取值范围，要注意挖掘隐含的限制条件，还要根据题设条件来进一步验证. 换元引参思想内涵丰富，如果学生能掌握上述这些方法，以后遇到类似的二元变量最值问题就可以顺利解决了.

[1]陈跃. 浅谈换元法在求最值问题中的应用[J]. 数学学习与研究，2015(19)：119.

[2]傅建红.从一道高考题看二元条件最值问题的求解策略[J].数学教育研究.2011(5)，55-56.