对一道高考模拟题的讲解展示与思考
2017-03-13甘肃省通渭县第二中学743300段伟军
甘肃省通渭县第二中学 (743300) 段伟军
对一道高考模拟题的讲解展示与思考
甘肃省通渭县第二中学 (743300) 段伟军
1.试题呈现
试题 (2016年定西市第三次高考模拟试题)设函数f(x)是定义在D上的函数,若对任何的实数a∈(0,1)以及D中的任意数x1,x2,恒有f(ax1+(1-a)x2)≤af(x1)+(1-a)f(x2),则称函数f(x)是定义在D的H函数.
(2)已知函数f(x)是R上的H函数,m是给定的正数,设an=f(n),n=0,1,2,…,m,且a0=0,am=2m,记Sf=a1+a2+a3+…am,对于满足条件的任意函数f(x),试求Sf的最大值;
(3)若f(x)是定义域为R的函数,且最小正周期为T,试证明f(x)不是R上的H函数.
2.课堂教学展示
2.1 复杂繁琐的讲解过程
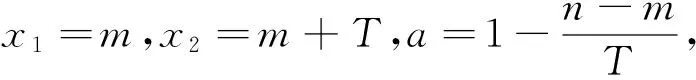
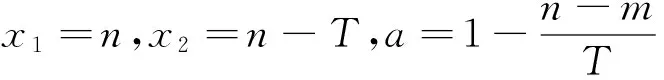
所以函数f(x)在[0,T)上是常函数,又因为f(x)是周期为T的函数,所以f(x)在R上是常函数,这与f(x)的最小正周期为T矛盾.所以f(x)不是R上的H函数.
2.2 学生的积极思考给予灵感
讲解过后给学生留了5分钟思考时间,问学生有没有其它问题,这时学生A举手说,老师你的这种思路我不是很理解,但他觉得可以从最小正周期找出矛盾,我给与评价性的指导,学生B举手说,我有其他证法,证法如下:
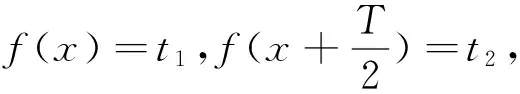
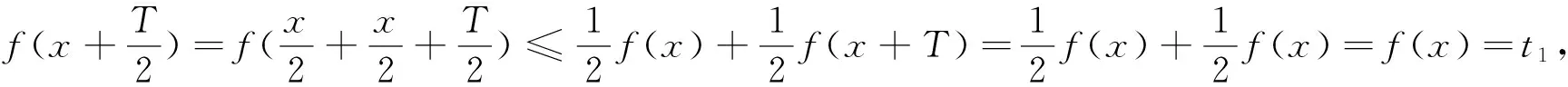
学生C回答,我是通过图像做的,H函数与老师讲过的凸函数差不多,应该向下凸的.
学生D举手回答说,如果函数是H函数,以幂函数指数大于1为例,图像在第一象限的部分各点处的切线斜率是递增的,我是从单调角度证明并找出矛盾的.证法如下:
假设f(x)是H函数,则f′(x)单调递增,设0
笔者在课堂上肯定了这位同学独特的见解,并给与积极的评价,同时指出这种证法缺少严密性,但结论是正确的.
2.3 适当的拓展引申使问题锦上添花
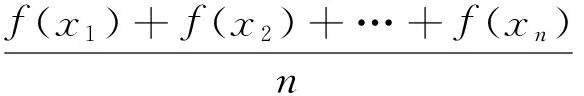
通过这七位同学的独特见解,使问题一石激起千层浪,学生意犹未尽,充满激情与渴望.
3 课后的感悟与反思
3.1 压力是动力
要解决数学中的难题,教师认真的研究试题是讲题的必要条件,认真研究问题,研究解法,研究变式拓展,研究学生解题中的难点与疑点,研究学生思维断层的原因,只有经过认真的研究,教师在课堂讲题时才能充分流露解题的思维过程,才能让学生举一反三,触类旁通,学生才能游刃有余,笔者研究了解答,没有考虑其他解法,而学生的奇思妙想给予我压力,这也说明我们忽视学生,过分依赖于答案,尤其高三试题训练时期.教师应该成为数学课题探究的创造者,有开阔的数学视野,了解高等数学与高中数学有拓展的内在联系与思想.认真思考试题本身蕴含的问题,加深对数学的理解,提高数学能力,为指导学生进行探索、探究做好充分的准备,“教师要成为学生进行数学探究的组织者、指导者、合作者.适时地为学生提供丰富的数学课题探究案例和背景材料;要引导帮助学生而不是代替学生发现与提出探究课题,尤其要鼓励学生与启发学生独立的发现问题,提出问题解决问题.
在学生探究问题上,教师一方面要鼓励学生独立的思考,帮助学生树立克服困难的勇气与毅力,另一方面要指导学生在独立思考的基础上学会合作,这包括与教师的合作.要实现这些要求,需要付出更多的时间与精力去研究便于学生理解与记忆的解题方法,这是一种压力,也是课堂教学的动力.
3.2 预设演绎别样精彩
教师在备课时应考虑预设各种课堂的生成.在课堂的实际教学中会出现意料之外的局面,包括学生的想法,问题的演变拓展,新课标把生成看做课堂的一种追求.有了预设,课堂的生成更有活力,课堂的教学更加充满灵气与智慧.预设成为课堂的动力与能量,在典型问题的引领下,激发学生的思维,教师只有预设才能机智的生成课堂效果,提高课堂效率.只有预设课堂才会并重、交融;才会和谐、自然统一.
