问题出在哪儿

☉湖北秭归县教育科研信息中心 何训光

☉湖北宜昌市夷陵区教师教育教学研究中心高先敏

☉湖北秭归县郭家坝中学颜昭英

问题出在哪儿

☉湖北秭归县教育科研信息中心 何训光

☉湖北宜昌市夷陵区教师教育教学研究中心高先敏

☉湖北秭归县郭家坝中学颜昭英

试题再现：已知AC=AE，∠BAD=∠EAC=∠EDC.

（1）如图1，若△ABC中，∠B＜90°，D为BC上的一点，点E在△ABC的外部，求证：AD=AB.

（2）若△ABC中，∠B＞90°，D在CB的延长线上，点E在△ABC的下方，则（1）的结论是否仍然成立？若成立，请在图2中画出图形，并加以证明；若不成立，请说明理由.

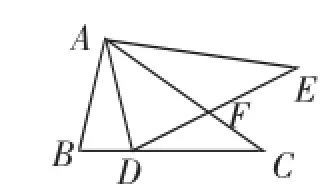
图1

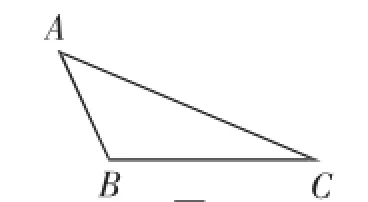
图2

这是某地八年级上册《长江全能学案同步练习册》中的一道题，是在学生学习了全等三角形四个判定方法后选配的一道习题.命题者意图很明显：以全等三角形和全等变换为背景，目的是培养学生基本的画图能力和全面提升学生的推理论证能力.

此题的第（1）问很简单，学生也都能正确解答，但是第（2）问的答案却是五花八门，很多老师都没有当一回事而默认了学生的错误解答，这样的错误若流传下去，会对学生产生什么样的不良影响？这题的错误又在哪里？为什么连教师都难以发现问题或错误产生的原因？

还是先请读者找一找下面给出的学生解答和他们所画图形的错误在哪里.

笔者调查了部分师生，很多师生是这样思考的：因为AE=AC，所以可以通过在图2的基础上把AE绕A顺时针旋转来画出需要的图形，当AE旋转到图3时，此时E与C正好重合，显然与点E在△ABC的下方这个条件不符，故舍去；再继续旋转到图4所示的位置，此时EA在∠BAC的内部，点E在△ABC的下方，符合题意；继续旋转到图5所示的位置，此时E正好落在∠BAC的AB边及其延长线上，也符合题意；再继续旋转便得到图6，此时AE在∠BAC的外部.所以，此题应分三种情况来证明.

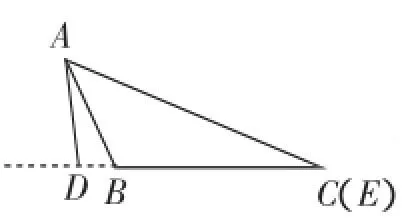
图3

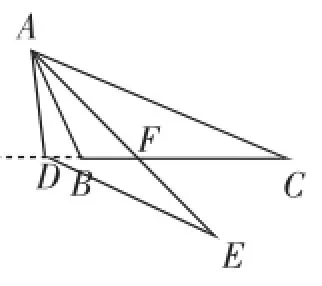
图4

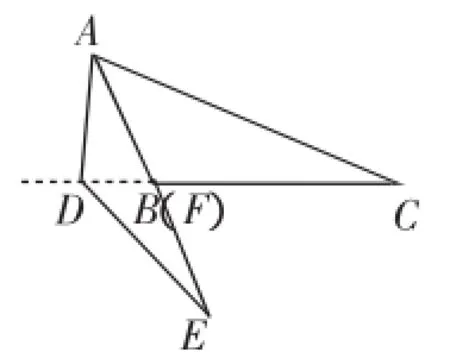
图5

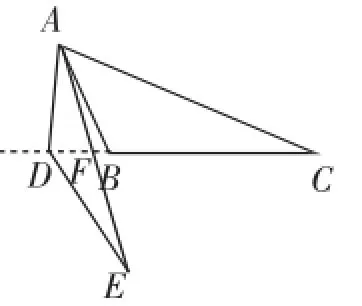
图6

（2）证明：（i）AE在∠BAC的内部.

如图4，设AE与BC交于点F，因为∠EAC+∠C+∠AFC=∠EDF+∠E+∠DFE，而∠EAC=∠EDC，∠AFC=∠DFE，所以∠C=∠E.因为∠BAD=∠EAC，所以∠BAD+∠EAB=∠EAC+∠EAB，从而∠DAE=∠BAC.又已知AC= AE，所以△ABC≌△ADE，从而得到AB=AD.

（ii）AE在∠BAC的AB边及其延长线上.

如图5，同（i）可证得∠C=∠E.又因为AC=AE，所以△BAC≌△DAE，同样可得到AB=AD.

（iii）AE在∠BAC的外部.

如图6，设AE与DC交于F，同（i）可证得∠C=∠E.又因为∠BAD=∠EAC，所以∠BAD-∠EAB=∠EAC-∠EAB，从而∠BAC=∠DAE.又已知AC=AE，所以△BAC≌△DAE，同样得到AB=AD.

以上给出的是学生中比较完整的解法，还有很多学生的解答就是以上三种情况中的一种，当然，多数师生画的图为图4或图6，其解答是第（i）种或第（iii）种情况的证明过程.

错因分析：初看起来，解答者考虑问题全面，思考问题过程中把各种不同的情况全部作了分析，而且因为后面符合题意的三种情况的证明方法和过程有不同之处，所以把三种情况进行了分类证明，三种情况的证明也步步推理严密、有根有据.看起来似乎很完美.

但是，只要读者仔细观看一下学生所画的图4至图6，不用分析就可以发现明显的错误，即可以明显地看出AD≠AB，或者说可以明显看出AB＞AD.

那么问题到底出在哪儿呢？

此题是要在给定的图2上画图，即说明图2是固定图形，题目还要求D在CB的延长线上，点E在△ABC的下方，那么这个图形就不能是随便一画或任意一旋转AE就能符合题干条件的.因而只能靠推理来画出图形.

多数师生是从先定E点，即从已知AE=AC来确定E点出发画图的，那么这样的E点是有很多的（以A为圆心、AC的长为半径，且在△ABC的下方的圆弧上的所有点），若在△ABC的下方的圆弧上任意取一符合AE=AC的点E，那么接下来就只能在AE的左侧作∠AED=∠C，使ED交CB的延长线于D点，再连接AD，这样虽然有∠EDC=∠EAC，但不能保证∠BAD=∠EAC也成立，如部分师生所作的以上的图4至图6都可以保证∠EDC=∠EAC，但都不能保证∠BAD=∠EAC.上面解答的错误就在于学生自己随便画一个图形并且承认它符合题干的所有条件，这样的情况若有，也只能是某种巧合或者说是某种特殊图形的情况，并没有一般性，更不能作为已知条件而当作证明的依据.这就是以上各种所画图形和证明不正确的根本原因.

由此可知：从点E出发作图不能保证原题干中的已知条件都成立.

这样，我们就只能从先找点D出发来画图了，要使AD=AB，且D点在CB的延长线上，那么这一点只能是在以A为圆心、AB的长为半径的弧与CB的延长线的交点（如图7中的点D），除这点和点B以外的其他任何一点都不会有“AD=AB”.所以D点也不是随便就可以画出来的，它是CB的延长线上唯一的一点.接下来确定E点，在AC的左侧作∠EAC=∠BAD，再在∠CAE的AE边上截取AE=AC，从而得到AE（如图7），再连接DE，这样连接虽然不能直接看出“∠EDC=∠BAD或∠EDC=∠EAC”，但是可以证明其相等.并且这样作出来的图形应该是唯一的，是不需要通过分类讨论来证明的.

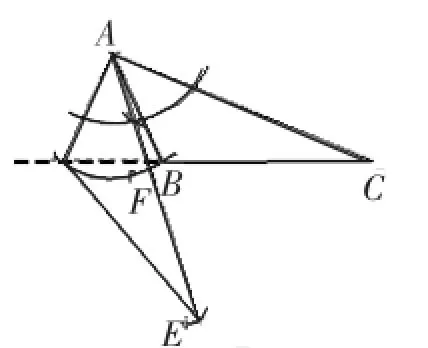
图7

那么此题到底如何来解答？笔者认为关键是要能画出图形来，图形画不出来，也就不能正确解答.下面笔者就从“先作图、再说理、最后证明”的方法来解答此题.

（2）解：当∠B＞90°，D在CB的延长线上，点E在△ABC的下方时，AB=AD仍然成立.

作图：以A为圆心、AB的长为半径画弧交CB的延长线于点D，再以A为顶点、AC为一边，在AC的左侧作∠CAE=∠BAD，并在AE上截取AE=AC，再连接DE.图7即为所画图形.

由作图可知：AC=AE，∠BAD=∠EAC.

则∠BAD-∠BAE=∠EAC-∠BAE.

即∠DAE=∠BAC.

又所作线段AD=AB，则△BAC≌△DAE，∠ADB=∠ABD.

则∠ADE=∠ABC.

则∠ADB+∠BDE=∠ADB+∠BAD.

则∠BDE=∠BAD，则∠BDE=∠EAC.

所以，以上所作的图形既满足原题题干中的已知条件“AC=AE，∠BAD=∠EAC=∠EDC”，也满足该问中的附加条件“∠B＞90°，D在CB的延长线上，点E在△ABC的下方”，按上述第（iii）种方法即可证明结论成立.证明过程略.

到此，本题应该是解答完毕，但还得回答老师一个问题.

问题：有没有“AE在∠BAC的AB边及其延长线上或AE在∠BAC的内部”的情况？

这就要看给定的钝角三角形ABC了，如图8或图9所示的钝角三角形ABC就是AE在∠BAC的AB边及其延长线上或者AE在∠ABC的内部的情况，但这样的情况也只一种，绝对不会同时出现三种情况.

这样的钝角三角形ABC，我们可以按如下的方法作出来：

先任意画一个等腰锐角三角形ABD，使AB=AD，再把BD向两侧延长；以A为顶点、AB为一边在AB的右侧作∠BAC=∠BAD，使边AC交DB的延长线于C，再在线段AB的延长线上截取AE=AC，连接DE，这样就能画图8所示的图形了.读者可以按上述方法画出图9所示的图形.

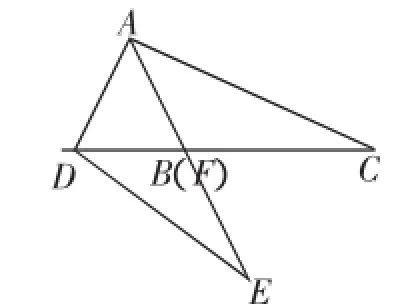
图8

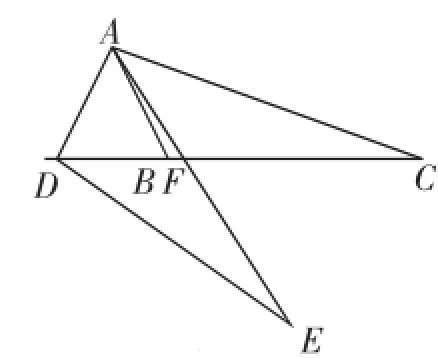
图9