设计教学需要“三种慧眼”
——读“跟随佐藤学做教育”有感
2017-03-11江苏无锡市雪浪中学王韶荣
☉江苏无锡市雪浪中学 王韶荣
☉江苏无锡市滨湖区教研发展中心王华民
设计教学需要“三种慧眼”
——读“跟随佐藤学做教育”有感
☉江苏无锡市雪浪中学 王韶荣
☉江苏无锡市滨湖区教研发展中心王华民
教育问题的复杂性,决定了研究教育问题需要不同的视角,佐藤学曾经用三种比喻来形容教育研究的视角,他认为:教育研究如同是用眼睛在观察世界,不同的眼睛就代表不同的研究视角,最基本的三种视角是“飞鸟之眼”“蜻蜓之眼”“蚂蚁之眼”,笔者觉得这种比喻既形象又贴切.飞鸟高翔天空,自由自在,但它们多是俯瞰,视角虽开阔,却并不集中,所谓高瞻远瞩却浮光掠影.蜻蜓也善于飞翔,但飞翔的高度比飞鸟要低得多,它们常常会停下来歇息,与飞鸟相比,蜻蜓比较接地气.蜻蜓之眼固然重要,但也会存在一些误区,所谓蜻蜓点水、浅尝辄止.与飞鸟、蜻蜓相比,蚂蚁显得微不足道,它们个头小,每天成群结队在地表或地下爬行,知道哪里有喜欢的食物,知道地下多深处有水源.蚂蚁的视野虽不宽广,但它们却精心地改变脚下的土地,它们的视角对于研究者来说,不可或缺,也难能可贵.
教学设计是根据课程标准的要求和教学对象的特点,将教学诸要素有序安排,确定合适的教学方案的设想和计划.一般包括教学目标、教学重点和难点、教学方法、教学步骤与时间分配等环节,是一个系统工程.从观察和解决问题的视角分析,需要“三种慧眼”——“飞鸟之眼”“蜻蜓之眼”“蚂蚁之眼”的结合.教研员王华民老师在无锡格致中学执教一堂公开课,课题:初三专题复习“数形结合”,该班学生层次比较高,他尝试按“三种慧眼”设计教学,取得良好的效果,以下将教学设计及思考与同行分享.
一、按“飞鸟之眼”进行宏观设计
“飞鸟之眼式”所研究的是宏观层面的问题,譬如,教学设计的立意和教学的主要内容.初三中考的第二轮复习,旨在强化重点、考点,注重知识的纵横联系,提升用数学思想方法解题的能力.它是专题复习,需要根据学情设置.从学生前期试卷检测看,部分学生利用图形解题的意识淡薄,用代数手段解决几何图形问题意识不强、不够清晰,而数形结合对于初、高中教学,都是一种非常重要的思想方法,因此设定“数形结合”专题.本专题的立意,其一,从中考的角度设计教学目标,能用数形结合的思想方法去分析,进而解决一类数学问题;在探索过程中体会由数想形,由形思数,增强数形结合的意识.其二,从初、高中衔接的角度设计.教学的经历和实践表明,有不少学生害怕高中数学,因此,从教学内容上消除学生的“怕”的心理,就显得尤为重要.所以,既要考虑初、高中数学的衔接点(知识、方法),还要考虑如何提升学生数学学习的自信心,为初三学生顺利进入高中学习奠定基础.
二、按“蜻蜓之眼”进行中观设计
按“飞鸟之眼”进行宏观设计后,接下来就要考虑中观设计.“蜻蜓之眼式”聚焦思考一些中观层次的问题.以专题复习课的教学设计为例.其一,要考虑选择哪些具体问题来表达主题——“数”有困难则用“形”,“形”有困难就用“数”,重点是选编例、习题.其二,考虑导入的问题情境.方案1,请同学们谈谈对“数形结合”的认识.因为数形结合的内容散落在教学内容中,学生通过自己的例举,能唤起回忆,其不足点是可能时间会超出.方案2,为了使得学生容易进入状态,能突出“数”和“形”是同一个内容的不同表示,可选择一道中等偏易的问题.其三,考虑问题呈现的顺序.最后确定,用1道导入题,2道热身训练题,3道典型例题及变式,2道练习巩固,再进行小结反思.当然,这些问题的设置要考虑学情,在学生的最近发展区内进行.
具体设计及说明如下:
1.导入问题.
师:如图1,这是一个熟悉的函数图像,请说出具体的解析式.
通过提问与追问,促学生回忆出函数有三种表示:解析式、图像和表格.
评注:由一个熟悉的函数图像,通过提问与追问,促学生回忆出函数有三种表示,让学生明晰“形”与“数”是同一个函数的不同呈现,当学生的观察与思考进入状态之时,便达到了教学立意的“数形结合”之目的.
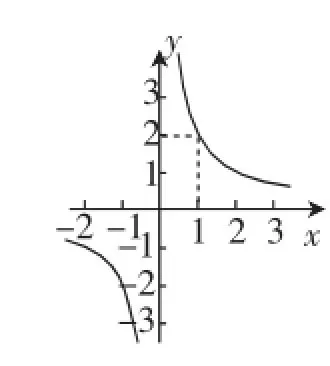
图1
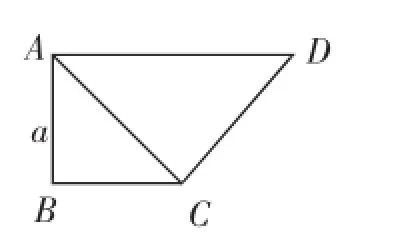
图2
2.热身训练,
(1)如图2,在四边形ABCD中,AD∥BC,∠BAD=∠ABC=90°,AD=2BC=2AB=2a,求证:AC⊥CD.
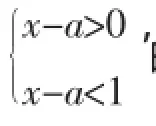
评注:热身训练(1)选取了高中立体几何中利用平面几何证明垂直的一例,它是通过以算(代数运算)代证.无论是“由形得角”还是“由形思数”,都让学生经历了探索、思考、发现的过程.热身训练(2)与其说是教师把学生由数向“形”上引,不如说是学生自我内省而逼其上“形”.通过这组“热身训练”,带领学生步入思维的快车道.
3.典例分析.
例1当-1≤x≤1时,函数y=ax+2a+1的值有正有负,则实数a的取值范围是________.

图3
(“数”→“形”)
例2二次函数y=ax2+bx的图像如图3所示,若方程ax2+bx-m=0(m≠0)有两个不等的实数根,则m的取值范围是________.
(“数”→“形”)
变式1:若|ax2+bx|=m(m≠0)有两个不等的实数根,则m的取值范围是________.
变式2:若|ax2+bx|=m(m≠0)有四个不同的实数根,则m的取值范围是________.
例3(2005年无锡中考改编)如图4,已知矩形ABCD的边长AB=2,BC=3,点P是一动点(P异于A、D),Q是BC边上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.

图4
(1)求证:△APE∽△ADQ;
(2)当P在何处时,△PEF的面积取得最大值?最大值为多少?
(“形”→“数”)
评注:本节课对例题的价值进行了充分挖掘,通过变式,变中求同,揭示了“数”与“形”之间的联系,使学生熟悉“数”与“形”间的相互转化,加深对知识的理解与内化.
4.当堂练习.

图5
(2)【挑战自我】(2000年北京春季高考题)已知函数y=ax3+bx2+cx+d的图像如图5所示,则().
A.b<0B.0
操作:告知学生,这是近年来高考试卷中普遍公认的一道好题.通过以下问题引导学生.
①从图像上你能获得什么信息?假设哪种形式合理?(过三点,设y=a(x-x1)(x-x2)
②通过二次和三次的类比,你能假设这个三次函数吗?
(法1)设该三次函数为:y=ax(x-1)(x-2)(*),展开得y=ax3-3ax2+2ax,与原函数比较,得b=-3a;挖掘隐含条件,如当x=3或4时,y>0,代入(*)得a>0,故b<0.
(法2)由二次函数中常用自变量0、1、-1对应函数值,类比到三次函数,得d=0、a+b+c+d=0且-a+b-c+d<0,两式相加得2b<0,则b<0.
解后回顾:教师引导学生体悟“类比法”“挖掘隐含条件”.
5.课堂总结.
通过本节课的学习,谈谈你的收获与认识.可从以下两方面进行:
(1)数形结合于解题有什么作用?你将采取什么自觉行动?
(2)数形结合对你认识问题有什么启发?
6.课外作业.(略)
评注:本节课的“当堂练习”有意选编了一道高考题,对学生而言,是“挑战自我”“拓展提升”,需要有“借我一双慧眼”的策略,就教学而言,更是“授人以渔”.一道优秀高考题被学生用初中方法解决,极大提振了学生学数学的信心.小结时让学生明晰、回味,既有方法层面,也有意识、能力层面,还有对事物的认识层面.
三、按“蚂蚁之眼”进行微观设计
我国古代著名哲学家、思想家老子有句名言:“天下难事,必做于易;天下大事,必做于细”,它精辟地指出了想成就一番事业,必须从简单的事情做起,从细微之处入手.通过中观设计,主体框架搭好了,问题、例题、习题及变式选编好了,接下来,还需要对一些教学细节进行微观设计.
在导入图形的问题后,要结合学生的回答,设计追问:你是怎么做的?你能说出这样做的理由吗?促学生回忆出函数有三种表示,得出函数解析式(数)与图像(形)是一一对应的.
热身训练(1)的具体操作,考虑请2—3名学生回答,暴露2—3种方法;热身训练(2)的具体操作,引导学生通过画数轴求解,并根据学生情况,适当板书.
在典例分析环节,例1的具体操作,要根据学生情况,指导其审题,抓关键词:-1≤x≤1、有正有负;提醒学生在端点处要另外监控.例2视课堂情况呈现1或2道.例3是第一道解答题,规范板书不能少,但考虑到时间因素,只板书要点.
之后的解后回顾,教师请学生体会华罗庚的名句“形缺数时难入微,数缺形时少直观.”
在呈现“挑战自我”后说明:从图像上挖掘隐含信息,渗透类比思想.对于课堂总结,可以考虑让2—3位学生表述,让学生体会,教师再小结投影.
综上所述,一节好的教学设计是一项复杂的工程,既需要宏观把握其目标、框架,实现精彩生成(有“飞鸟之眼”),在廓清认识、厘清思路的基础上精心设计、合理组织(有“蜻蜓之眼”),还需关注细节,进行微观雕琢(有“蚂蚁之眼”),是“三种慧眼”的有机结合.唯有如此,才能取得理想的教学效果.
1.王华民,庞彦福,何勇.探索·思考·策略·引领——初三专题复习“数形结合”教学设计及评析.[J]中学数学(下),2014(11).
