变式理论在教学中的自然应用探究
2017-03-11江苏苏州市苏州高新区第二中学
☉江苏苏州市苏州高新区第二中学 张 静
变式理论在教学中的自然应用探究
☉江苏苏州市苏州高新区第二中学 张 静
陕西师范大学罗增儒教授曾经说过:“教师在教学中应当注意相机而诱导,而不仅仅是全盘打算和细节处理.”这里说说的“相机而教”就是适时点拨、延伸、变式.所谓“点拨”,是在学生疑难处入手,给学生以方法上的指导和引领,让学生在这样的启发下去发现问题与解决问题;而“诱导”则是方法上面的指导,这样的指导是有利于学生思路的打开的,使学生从获取知识转化为获取技能;“变式”是学生把数学题去其个性,留其共性,找到解决问题的通法与自然解法.那么在课堂中我们该如何处理,以期达到课堂的优效与实效呢?
一、思路点拨——从疑难处着手


图1
同理可得:B4(12,2),B6(18,2)……
所以,B2016的横坐标为:1008×6=6048,所以,点B2016(6048,2).
当学生一筹莫展时,教师应该进行思路的点拨与指导,帮助学生确立思路和解决问题的方式和方法,从而有效地突破难点,顺畅解题,只有这样,才能让学生的知识、技能与情感得到锻炼与提升,进而使我们的课堂更有效.
二、变化与聚焦——从图形问题上找突破
原题:在3×3网格中有9个相同的小正方形,每个网格图中有3个小正方形已涂黑,请在余下的6个空白小正方形中,按下列要求涂黑:选取1个涂黑,使4个黑色的小正方形组成一个不是中心对称图形的轴对称图形.
变化1:选取1个小正方形涂黑,使4个涂黑的小正方形组成的图形不是轴对称图形的中心对称图形;
变化2:选取2个小正方形将它们涂黑,使形成的图形组成一个轴对称图形.

图2

图3
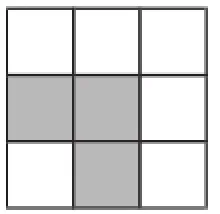
图4
分析:(1)根据轴对称图形的定义作图即可;(2)根据中心对称图形的定义作图即可;(3)根据轴对称图形的定义作图即可.
原题:

图5
变化1:

图6
变化2:
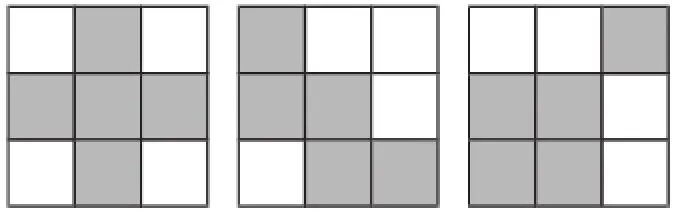
图7
换一种眼光看待数学问题,换一种方式解决数学问题,真正掌握了正确的方法才能明道!教师在教给学生知识的同时,也要教给他们全面读题的方法与视角,以期能有智慧的碰撞,进而获得基本技能与更高层次的能力.同时,在进行变式教学的过程中,如何对问题进行细致的挖掘也是一项很重要的技术活,不断地进行揣摩才能有真正的突破.
三、功到自然成——知识核心处变式
原题:如图8,已知四边形ABCD是梯形,AB=3,BC=4,AD=1,AD∥BC,AB⊥BC.若线段AB上有任意一点P,延长PD到E,使2PD=DE,作平行四边形PCQE,使PE、PC为其两边,那么线段PQ存在最小值吗?如果存在,请求出最小值.
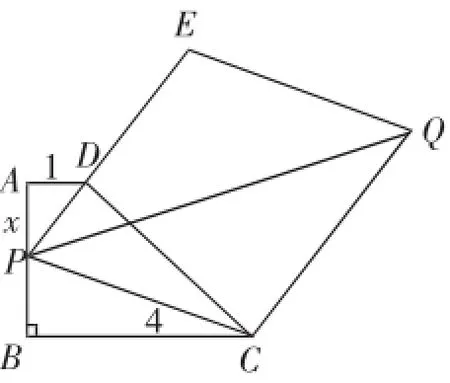
图8
方法解析:
法一:过点Q作QG⊥BC,过点P作PF⊥QG,垂足分别为点G、F,再过点E作ER⊥PA(如图9).
解:设PA=x,BP=3-x.
由于DE=2PD,易得RE=3,RA=2x.
易证△PRE≌△QGC,则CG=RE=3,PR=EG=3x,则FQ=3x-(3-x)=4x-3.
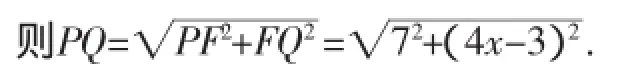
则当x=0.75时,PQ取得最小值7.

图9

图10
法二:设PQ交DC于点M,过M作MN垂直于AB,过Q作QG垂直于MN(如图10).

显然,求线段的最小值,我们可以用代数的方法,可以用函数求最值法来求,也可以用几何的方法,用“垂线段最短”,从特殊的位置入手,加以分析与解决.
变式:(2013年中考第18题)已知点A(8,0)、B(0,6)、C(a,-a)与点D是平行四边形的四个顶点,请求出CD的最小值.
显然本题中点C在直线l(第二、四象限角平分线)上运动,而点D随着点C的运动而运动,那么本题也是求两个动点间的最小值,与上题的解法应该有着异曲同工之效.
分析:不妨进行如下的分类讨论来解决这一问题:(1)若这个平行四边形以AB为边,那么CD的值就是一个定值10;(2)若以AB为平行四边形的对角线,CD必过AB的中点E,要求CD的最小值,可以利用二次函数求最值的方法来求解.
解法:如图11,只要表示出点C、D的坐标.由于A(8,0)、B(0,6),则点E的坐标为(4,3).又点C的坐标为(a,-a),则点D的坐标为(8-a,6+a).
触类旁通:那么,是否还可以进行其他的方法尝试呢?如图12,建立这样的平面直角坐标系来解决这一问题.

图11
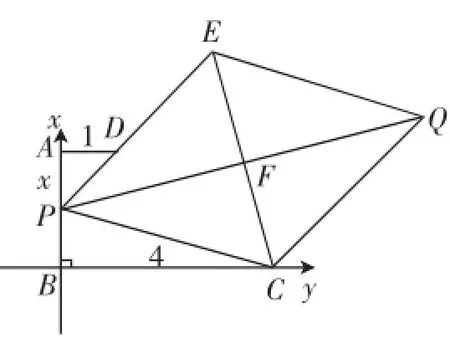
图12
设AP=x,则点P(0,3-x)、C(4,0).由DE=2PD,易得点E(3,3+2x).
将上述看似毫无联系的题放在一起,其目的是为了让学生透过数学题的表象,看到两道题的本质,都是求线段最值问题,其常用方法不外乎几何法与函数法,然而建立了坐标系后,本题的难度与处理方法明显简化也好理解了,故通过两题的变式,我们更清楚地找到了解决的通法、特法与自然解法,进一步提高了能力.
裴光亚先生说:比知识更重要的是思想.只有有了思想,才能把知识转化为能力.我们的数学课堂就应当该出手时就出手,从给学生知识到渗透思想,再到培养基本技能,进而挖掘更高层次的能力,努力实现师生在课堂上的最佳表现.
