透过“影响”表象厘清“独立”本质*

透过“影响”表象厘清“独立”本质*

☉福建省厦门第一中学 王淼生

一、提出问题

前不久考试中有一道看似简单却引起争论的选择题，原题如下（下称案例1）：

案例1现有以下三个命题：

（1）掷一枚质地均匀的骰子，事件M：出现点数为奇数；事件N：出现点数为偶数.

（2）袋中有大小相同的5个红色、5个黄色，依次不放回地摸两球.事件M：第1次摸到红球；事件N：第2次摸到红球.

（3）分别抛掷2枚均匀硬币，事件M：第1枚正面向上；事件N：两枚结果相同.

其中事件M与事件N相互独立的有（）个.

A.3B.2C.1D.0

命题专家给出的答案为D.

二、剖析缘由

对于（1），容易判断事件M与事件N是对立事件，显然不是相互独立事件.对于（2），因不放回，显然事件M发生对N有影响，故事件M与N不是相互独立.可对于（3），老师们之间产生较大分歧，争议的焦点在于：事件M的发生对事件N的发生是否有“影响”.

观点1：一部分教师观点如下：文［1］将“事件的相互独立性”编排在“条件概率”之后，也就是说“事件的相互独立性”是紧接着“条件概率”之后学习的.而条件概率的本质就是事件M的发生对事件N的发生有直接“影响”，故而形象地记作P（N|M），因此独立事件的核心就是事件M的发生对事件N的发生没有“影响”.简而言之，事件之间没有“影响”就是独立事件.这是一线教师普遍观点，正是从这个指导思想出发，上述（3）中事件M发生前提下，事件N只发生“正面、正面”一种情况，从而认定“影响”了事件N发生，因此判定（3）中事件M与事件N不是相互独立.

观点2：另一部分教师观点如下：两个事件是否独立，不能仅仅凭表面是否“影响”，而是要通过具体的计算才能确定，即需要验证：

P（MN）=P（M）P（N）.①

若满足上述①，则相互独立；否则，不是相互独立.事实上，由计算易得

显然满足上述①，说明上述（3）中的事件M与事件N相互独立，故答案为C.

表面上看，争议的焦点似乎答案到底是选C还是D的问题，其实质在于厘清判断独立事件的标准是什么？理论依据是什么？

三、厘清概念

1.模棱两可——质疑是研究的源动力

笔者觉得观点似乎有道理.因为没有事件M时，事件N包含“正面、正面”与“反面、反面”两种情况.而在事件M发生的前提下，事件N只能发生“正面、正面”这一种情况.事实明摆着：事件M的发生对事件N的发生确实有“影响”，这是不可否认的.但上述观点2是通过定量计算，符合中学教科书（文［1］）独立性定义，显然是正确的，不容置疑.哪到底哪一种观点正确呢？

2.精准定义——概念教学的首要原则

美国加州伯克利大学伍鸿熙教授认为概念教学有五个相关联的基本原则，其中首要原则就是概念必须精确定义.遇到棘手问题，尤其涉及概念问题，一线教师首先想到的是仔细、慎重、全面查阅该概念的原始定义，当然是从最权威的教科书入手.

文［1］（中学教科书）第54页是这样定义独立事件的：

定义：设A，B为两个事件，若P（AB）=P（A）P（B），则称事件A与事件B相互独立.

文［2］（大学教科书）第21页的定义与文［1］完全相同，而且文［2］还给出以下定理：

定理：设A，B为两个事件，P（A）＞0，P（B）＞0.若A，B相互独立，则P（B|A）=P（B）；反之亦然.

上述定义与定理为判断独立事件提供了理论依据，同时也是具体操作步骤.

依据：当P（A）＞0，P（B）＞0，则有事件A，B相互独立⇔P（AB）=P（A）P（B）.②

上述②并不奇怪，因为数学定义中很多就是充要条件.据此可知上述观点2正确，毫无疑问案例1的答案为C，也就是说上述案例1中的（3）中事件M与事件N相互独立.

其实，上述案例1中的（3）并非新题，在教科书上可以找到“影子”，比如文［1］第55页第1题，还有文［2］第20页例1，原题如下（以下分别称案例2、案例3）：

案例2分别抛掷2枚质地均匀的硬币.设“第1枚为正面”为事件A，“第2枚为正面”为事件B，“2枚结果相同”为事件C.试问A，B，C中哪两个相互独立？

案例3设试验E为抛甲、乙两枚硬币，观察正反面出现的情况.设事件A为“甲币出现正面”，事件B为“乙币出现正面”.试问事件A与事件B是否相互影响？

3.深度剖析——厘清“影响”的本来面目

我们知道定量分析具有精确、严谨特征，但由于定量分析需要进行详细的推理、运算，因此过程略显复杂一些.相对来说，定性分析则简捷、明了，但遇到较为复杂的问题容易因表面现象蒙蔽而出现错误.其实，上述观点1就是定性分析，上述观点2才是定量分析.哪为何定性分析容易出现错误呢？到底问题出在哪儿呢？

查阅百度可知“影响”是指以间接或无形的方式来作用或改变人或事的行为、思想，哪具体到数学概念“独立事件”中的“影响”又该如何界定呢？

其实，我们平常所说的事件M发生是否“影响”事件N，不能仅仅从表面，不要以为事件N所含基本事件个数在表面上的减少就是受到了“影响”.上述观点1就是受表面诱惑，即“所含基本事件个数较少”而导致错误.当总的基本事件个数减少（即样本空间缩小）时，概率计算

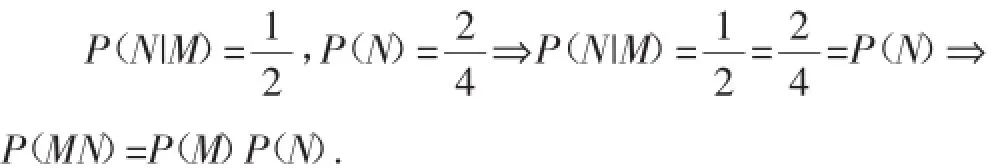
上述分子、分母确实发生变化，即表面上似乎有“影响”，但“成比例”变化，因而没有改变最终比值，即概率根本没有受到“影响”，故两个事件相互独立.

综上所述，独立事件中的“影响”并不仅仅是指“过程”，而是最终的“结果”；独立事件中的“影响”尽管影响了“表象”，但只要不妨碍最终的结果即本质，依然是独立事件；独立事件中的“影响”并不仅仅是指表面的基本事件个数（即样本空间）变化，而是指最终概率是否满足上述②.对于具体的独立事件相关问题，不能仅凭定性分析下结论，还要进行定量分析.从定性到定量分析不仅是实施宏观到微观的必由之路，而且是实现“估值”到“精算”的必经之道.因此上述②既是判断独立事件理论依据，也是判断独立事件具体操作过程.

四、感悟体会

公式中分母变小，还应该看到其分子同时也在相应减少.当分子、分母同时减少，只要其比值不变，我们就认为是不受“影响”，即认为是独立事件.

以上述案例1中的（3）为例，由计算可得

1.扪心自问——错误不是学生“专利”

数学学习和“错误”是一个相伴过程，“错误”是数学研究中永恒话题.不少教师以为这是学生的“专利”，其实教师也不例外（如文［3］）.从认知角度分析，教师在概念教学过程中犯错误是难免的.教师也是在不断地犯错、不断地纠错中成长的.正是因为教师对数学概念的理解出现偏差甚至错误，才能对数学概念的把握愈加精准，教师才会变得更加成熟.

“错误素材”是难得的、宝贵的教学资源.文［4］指出应该“照照镜”——教师深刻反思概念教学的失误之处，诚恳看作检查自己教学效果的一面镜子；“治治病”——顺着错误思路，深究错误起因、深挖错误根源、深思错误预防，从本源上找出“元凶”、铲除“土壤”，肃清“根基”，真正厘清概念、吃透概念.正如黑格尔指出：“错误本身乃是达到真理的一个必然的环节.”概念教学不仅是教学生的过程，更是教师提高自身业务水平，尤其是夯实自身功底的绝佳历程.难怪不少名家大师说“听听数学概念课就知道一名数学教师业务功力”是多么经典的感悟啊！

2.追根溯源——越辩论越清晰

数学显著特征之一就是高度抽象，这就决定数学概念的深奥.在集体备课中，教师之间需要辩论；在实施教学中，师生之间、生生之间需要辩论；在公开教学中，教师与专家、专家与学者之间需要辩论.上述案例1就在笔者备课组及教研组中展开激烈争论，观点1与观点2就是当时的真实记录.数学概念需要辨析，越辩越明、越争越清.概念既可以从“正面”辨析，也可以从“方面”即借助错误案例剖析，在“错误”中“辨析”，在“反例”中“争论’’.对于有些概念，反面案例更能一针见血剖析概念内涵，其效果甚至远远胜过正面案例（如文［4］）.笔者近年对概念进行了一些研究并取得一点成果（如文［3］～［8］等），其中文［3］、［4］、［7］被全文转载在人大报刊复印资料《高中数学教与学》.

3.概念教学——本质是“玩”概念

李邦河院士指出：“数学根本上是玩概念，不是玩技巧，技巧不足道也.”足以说明概念教学在数学教学中占据举足轻重地位.章建跃博士在文［9］中明确指出，概念教学研究是数学教育心理学的主要任务之一.数学概念表明所研究的数学对象“是什么”，这是“玩概念”的基础.没有对概念内涵的把握，对概念的性质研究就会成为无本之木、无源之水、无米之炊.从定性到定量地展开研究而获得数学概念的性质，这是“玩概念”的重要一步.只有这样才能构建概念与概念之间的纵横网络，才能真正理解概念.

数学概念是构建数学理论大厦的基石，是思维的细胞.但因受到篇幅限制，教科书历来惜字如金.对一些概念的表述有时仅仅一句话，甚至一个符号而已，这表面上给一线教师理解概念，尤其是把握概念的内涵增加了不少难度.但从另一个角度看，正是因为教科书没有详细解释，反而给一线教师留下无限的探究、思考空间，这正是我们常说的要吃透教材，深入解读教材，对教科书有独到的、创造性的剖析，从而达到适合自己也符合学生更顺应课改理念的个性化教学，这正是对章建跃先生提倡的“不是教教材而是用教材教”最佳诠释.

4.哲学原理——升华MPCK理论

自舒尔曼提出学科教学内容知识（PCK）理论，从而使数学教学知识研究从PCK泛学科研究中独立出来，成为专门研究数学学科教学知识（MPCK）理论依据，是数学教师从事专业教学所应具备的核心知识.MPCK不仅要求数学教师有厚实的专业素养（MK），还要有先进的教学方法策略（PK），还要有丰富的学科内容知识（CK）.从集合文氏图角度发现，MK、PK、CK越大，其交集部分也会越来越大，形成数学学科教学知识就会越来越丰富.笔者在教学一线忠实践行MPCK理论，越发感受到将这些知识有机融为一体的推动力正是辩证唯物主义哲学观，遗憾的是，数学教学中的哲学观还没有引起足够重视.数学教学，尤其是概念教学，不仅要有数学眼光，更要有哲学视野，以发挥哲学的灵魂与统帅作用.站在哲学高度来高屋建瓴地指导具体的数学学科教学，这正是MPCK理论升华与创新.

在上述独立事件中的“影响”折射了哲学原理：运动（如样本空间变化）是绝对的，静止（如比值不变）是相对的.动中有静，静中含动，动静结合，和谐统一.正是因为独立事件中蕴含着这一哲学原理，因此主编在编写教科书（文［1］）时特意将独立事件紧紧安排在条件概率之后，从一个侧面说明了独立事件也可以看作特殊条件概率，即当事件M发生前提下，对事件N发生的“影响”很小很小（比值相差很小），当“影响”小到几乎忽略不计时，我们就认为是独立，这正是辩证法量变到质变原理的具体体现.同样的道理，我们也可以将互斥事件看作特殊独立事件，即当事件M发生对事件N发生不仅有影响而且影响很大，大到足以让另一个事件不可能同时发生，我们就认为是互斥.尽管中学一线教师甚至不少专家学者都认为互斥与独立事件毫不相干.通过事物之间普遍联系观点，深刻揭示这些概念之间内在关联，这正是概念教学重中之重，这其中渗透了转化与化归、有限与无限、或然与必然等数学思想.像这样的案例在高中数学中处处可见，比如，切线是割线极限位置就彻底解决了一直困扰师生“切线与曲线的公共点个数问题”.其实切线与曲线的公共点可以是一个、二个乃至无数多个，换句话说，是否为切线与公共点个数毫无关系，由此进一步诠释了初中时所学的切线与圆只有一个公共点的特例只是表明圆是一种特殊曲线而已.再如，圆台上底面无限缩小的极限位置就是圆锥特例、圆台上下底面逐步相等时就是圆柱特例，这样就将三者紧紧联系在一起，从而有效地破解了学生记不住三者的侧面积、全面积、体积等一堆公式的烦恼.再如，圆锥曲线的原始定义，即动点到两个定点距离的和（差）为定值的点的轨迹是椭圆（双曲线），本身就蕴含着运动中有静止，静止之中时刻在运动，因此几乎所有的解析几何综合问题的最后落脚点都是涉及定值、定点问题就不足为怪，其本源就在于其自身定义本来就蕴含丰富的哲学观.再如，一直“折磨”一线教师的《任意角三角函数》为何与《解三角形》被教科书主编“活生生”拆开并被编排在不同的模块之中，就是因为任意角三角函数的产生并不是因为解三角形的需要，更不是初中锐角三角函数的推广，而是为了描述客观世界无处不在的周而复始、循环往复的周期现象，说到底，任意角三角函数是为研究“周期现象”而生，而圆周运动则是最佳的模型，因此新课标教科书采用“单位圆定义法”而摒弃长期以来并被大家熟悉的“终边定义法”就是顺应时代的发展、顺应课改的理念，这就是章建跃博士在很多文章、著作及讲座中一直呼吁一线教师回归三角函数本质的缘由所在.由此可见，在实施数学概念教学中不仅要渗透数学思想方法，更要加强辩证唯物主义哲学原理的有机融合，特别是联系与发展的观点、运动与静止的观点、量变与质变的观点，从而为MPCK理论注入新鲜血液，为数学概念教学奠定坚实基础.

1.中华人民共和国教育部.普通高中课程标准实验教科书数学选修2-3（人教A版）［M］.北京：人民教育出版社，2009.

2.盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京：高等教育出版社，2010.

3.王淼生.追寻三角学发展史领悟主编意图厘清教学困惑［J］.中国数学教育（高中版），2016（1-2）.

4.王淼生.概念教学不妨尝试“事后补救”［J］.中小学数学（高中版），2015（12）：40-43.

5.王淼生.论文《这个看似简单的概率题目，答案到底是多少？》［J］.数学通讯（教师刊），2014（1）：34.

6.王淼生.感悟课改理念洞察教材意图开展解题教学——从空间向量安排在立几中的先后次序说起［J］.中学数学教学，2014（5）：1-5.

7.王淼生.利用定积分概念解题的几个注意点［J］.中国数学教育（高中版），2014（5）：57-60.

8.王淼生.深刻领悟编者意图深入领会课标教材——对诱导公式的一点思考［J］.中学数学教学参考（上旬），2015（10）.

9.章建跃.如何理解“数学是玩概念的”［J］.中小学数学（高中版），2015（1-2）：封底.

10.王淼生.基于的数学概念教学策略——有意差错［J］.中学数学杂志（高中版），2016（9）.

11.王淼生.透过现象追根溯源看清本质［J］.中学数学（上），2015（12）.

*本文系全国教育科学“十二五”规划2015年度单位资助教育部规划课题“基于数学教学内容知识（MPCK）视角下的概念教学案例研究”（课题批准号FHB150464）研究成果.