小议多角度思考平面向量综合性问题

小议多角度思考平面向量综合性问题

☉江苏省宜兴市和桥高级中学 沈琴

高三数学二轮复习怎么演绎才能落到实效？综合问题纷繁复杂，如何解读才能细致入微？难题困难重重，怎么分析才能合情合理？这些都成为一线教师复习教学的困惑.在二轮复习教学中，我们经常会遇到这样的困惑：一方面是教学中讲的时间越来越短，因为各种各样的考试穿插其中，要把做的题目讲完不是易事；另一方面，很多讲过做过复习过的内容学生却越做越差.笔者认为造成这种情况的其中一个原因，是对知识点的总结和梳理不到位，无法合理通过有效的、典型的问题承载所要考查的知识核心.

我们知道，二轮复习主要是对知识点横向和纵向的链接，构建完整的数学知识体系，讲题目不在多，而在于精，应注重数学思想方法的渗透，在教学上注重阐述解题的思路及方法的运用.以知识灵活运用较强的向量章节为例，我们不难发现，向量的基本知识并不多，但是其知识的理解并不容易，比如，学生对于向量数量积的投影值的理解仅限于正数，负数和零则无法理解；平面向量基本定理中基底是什么？为什么要这么定义基底？正交向量与一般自由向量之间的关系是什么？向量数量积与向量和、差之间的本质关系？等等.笔者发现，学生对于这些反映向量本质的深层次的知识知之甚少.从向量问题解决的思考角度出发，代数化和图形化是向量问题最基本的两个解决路径，实际教学中我们不难发现学生对向量综合性问题往往是一片茫然.试想，连基本思想、导向都没能考虑到位，如何解决这些向量综合性问题呢？

一、知识的多角度

题目如何解，罗增儒教授把解题总结为“条件预示可知并启发解题手段，结论预告需知并诱导解题方向”.解题就是“找关系”——找出已知未知的联系，不断缩小以至消除二者之间的差距，从而达到解题目的.通过一题多解、渗透了函数与方程思想，参数方程思想，化归与转化的思想，使学生学会思考、掌握方法，有利于培养学生思维的广阔性与深刻性.

通过直观感知—观察—操作确认的认识方法理解并掌握用余弦定理解决问题，掌握函数与方程思想，寻找条件中的变量，设出变量.培养学生观察、探究、发现的能力，在题意中找到两个变量之间的关系，构造函数.让学生在观察、探究、发现中学习，理解向量作为一种工具引入高中数学的价值，在解题中体现向量的高效简洁，体验学习的乐趣，增强自信心，树立积极的学习态度，提高学习的自我效能感.

问题1如图1，在△PAB中，C，D是AB上两点，且AC= BD，∠CPD=90°，且PA2+PB2= 10，求2AB+CD的最大值.

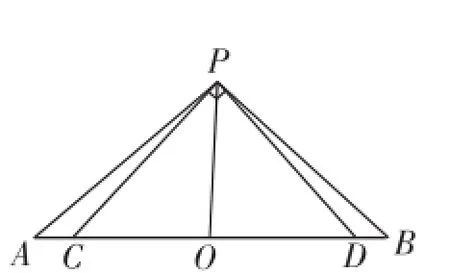
图1

分析：学生在经过一轮知识的系统复习后，对知识点都有了解，但是构建整个知识体系的能力还比较弱，不能做到对于相应知识的相对熟练的掌握，就无法做到信手拈来的最佳状态.本题笔者认为命题非常不错，题干短小精悍，题意明确，入口非常广，考查知识点明确，考查数学思想众多，但是运算量并不大，不烦琐，完全起到了考查学生能力的作用.重点是两个变量的引入与理解，难点是利用减元思想构建一元二次方程，创设平面向量中的情境，构造两个向量等式，在解题中利用参数思想等.引导学生寻找2AC与BD之间存在的变量关系，将所求的长度问题转化为两元变量最值问题.

思路1：设AC=BD=x，CD=y，则所求2AB+CD变成t=4x+3y，在△CPD中，设∠PCD=α，则∠CDP=-α.

在△CPA中，根据余弦定理有：

PA2=x2+PC2-2xPC×cos∠ACP，①

PA2=x2+PC2-2xPD×cos∠BDP，②

将上述①②转化为：PA2=x2+PC2+2xPC×cosα，③

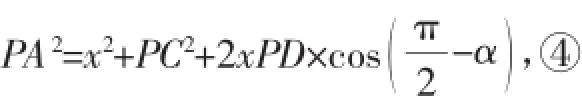
将③④两式平方相加可得2x2+PC2+PD2+2xPC×cosα+

所以可以得到2x2+y2+2xy=10.（*）

又设t=4x+3y，将其与（*）式联立，消去其中一个变量，不妨消去y，得到10x2-2tx+t2-10=0，Δ≥0，得t≤10.

思路2：作CD中点O，则由△CPD是直角三角形，所以|PO|=，利用平面向量知识构造⑦将上述⑥⑦两式平方相加后可得2x2+y2+ 2xy=10，（*）本思路中将不再运用方程求解，根据参数方程思想，将（*）式化为（x+y）2+x2=10，令x+y=cosθ，x=sinθ，则y=cosθ-sinθ，x=sinθ，所以t= 3cosθ+sinθ，由“合一公式”变形得到t=10sin（θ+φ），同样可得t≤10.

思路3：对学有余力的同学，可以介绍平行四边形对角线平方和性质，利用将三角形补全为平行四边形，进而利用该性质得到定值，结合柯西不等式求解.这种思路是问题本质的体现，是一种巧算，显然对于多数学生而言并不适用，但是点拨问题的本质，是为了引导学生思考更为深层次的数学知识.

说明：本题是填空中的压轴问题.也是结合平面几何知识的向量问题，而我们高中数学教学中，针对平面几何的知识点主要是正余弦定理或者平面向量，这两个知识点在整个复习中极易被忽视，事实上，我们仔细研读近年的《考试说明》和《考试大纲》，可以发现高考数学的考试要求，在“函数的奇偶性”、“函数的零点”、“平面向量的基本定理”等方面要求有所提高.平面向量的问题是最近几年必考内容，它是求角、距离等的重要工具，越来越受到重视.平面向量可以单独成题考查，也可以结合三角函数、正余弦问题来解决.要让学生掌握和熟练运用某个知识，教师就要有意识地给学生提供该知识应用的不同环境，学生只有在不同环境中，形成了自觉运用该知识的“思维定式”时，才可以说是真正掌握了知识.本题在解决过程中，创设了两种完全不同的情境，分别利用余弦定理和平面向量来解决问题，通过不同解法的比较，平面向量的工具性更加明显地突显出来，让学生在解题中自我比较，自我发现，才能更加深刻地去了解向量.平面向量之所以能在高中数学内容中占有一席之地，是因为其具有“几何形式”和“代数形式”的双重身份，既然教材中引入向量法，那我们就要将向量的特点充分发挥出来，而不是“穿新鞋走老路”.

二、思想的多角度

解决向量综合性问题，我们还可以从思想的角度架构.从思想角度来说，向量有两个重要的导向，其一是代数化，其二是图形化.教师可以思考，从培养学生数学素养的角度来说，哪种导向更为重要呢？显然对平面向量来说，图形化的导向更重要一些，其往往具备了揭示向量问题本质的特点，也体现了数形结合思想；随着学习的深入，代数化的特性才会在更高维度的向量问题中揭示出来，比如n维度的向量问题，只能通过代数的视角进行解决.举一个多角度复习的问题：

问题2设e1，e2为单位向量，非零向量b=xe1+ye2，x， y∈R，若e1，e2的夹角为，则的最大值等于________.

分析：问题以平面向量基本定理为载体，将向量夹角、模长运算、单位向量等相关知识综合.该题考查了平面向量的基本概念和综合运用，涵盖了单位向量、平面向量的基本定理、夹角、向量的模等体现向量特点的概念和定理.最值问题求解，体现了静中有动，题目简约而不简单.

图形化思路：不妨设x≠0，由b=xe1+ye2，x，y∈R

图2

说明：利用图形化，掌握图形变化的本质，结合数形结合，直观而简洁.

说明：笔者问过不少学生，学生都认为本题代数化手段远远优于图形化的思路，但是运算较为烦琐，而图形手段较为显然地揭示了何为模长最小的意义：垂线段最短！教学中，对于综合性问题复习，更要抓住问题所反映的知识本质.笔者以为从中学三维以下的问题而言，图形本质的揭示显得更为直观一些，也是我们教学更需要提倡的.

总之，平面向量综合性问题既需要从知识角度去思考，也需要从思想导向上去认识，将这些知识结合起来、思想串联起来，对于向量教学就有总的导向作用，在学习过程中也会产生较为明确的方向，更有利于我们的教与学.

1.宋卫东.从生“动”到生动，诠释思维品质的提升［J］.中学数学月刊，2013，5.

2.方厚石.向量教学诠释思维品质［J］.数学通讯，2014，1.

3.鲍建生等.向量教学研究［J］.数学教学，2013，1.