再磨过程的泵池液位和给矿压力双速率区间控制

王兰豪 贾瑶 柴天佑

选矿再磨过程是将一段磨矿浆和不合格的再磨矿浆进行再次磨矿分级的过程.在再磨的生产过程中,稳定泵池液位是保证再磨过程的安全运行的重要条件[1],稳定旋流器给矿压力是保证再磨分级效率的先决条件[2],因此再磨过程高效稳定运行必须保证泵池液位和旋流器的给矿压力都要达到控制目标范围内.

国外磨矿基本采用棒磨开路的定量给矿和配比给水的磨矿工艺[3].由于其矿石性质较国内稳定,使一段磨矿浆流量稳定,泵池液位波动小,采用定值闭环控制方式对泵池液位控制也不会使旋流器的给矿压力发生较大波动.文献[4]针对铜矿的再磨过程是以泵池补加水流量和矿浆泵的频率为输入,以泵池液位和旋流器给矿浓度为输出,采用多变量控制方法对泵池液位和给矿浓度进行定值控制.文献[5]针对镍矿再磨过程以矿浆泵流量为输入,以泵池液位为输出,采用预测控制方法对泵池液位进行定值控制.上述控制方法[4−5]通过工业应用实验说明文献[6−7]针对金矿的再磨过程方法的有效性.以矿浆泵频率为输入,以泵池液位为输出,分别采用PID控制方法和模糊控制方法对泵池液位进行定值控制.文献[8]针对金矿磨矿过程,以泵池出口流量为输入,以泵池液位为输出,采用分数阶PI控制方法对泵池液位进行定值控制.文献[9−10]针对金矿磨矿过程,以矿浆泵频率和泵池补加水流量为输入,以泵池液位和旋流器给矿浓度为输出,分别采用非线性模型预测控制方法和鲁棒非线性模型预测方法对泵池液位进行定值控制.文献[11]针对铂矿磨矿过程,以泵池出口流量和泵池补加水流量为输入,以泵池液位和旋流器给矿浓度为输出,采用多变量控制方法实现对泵池液位定值控制.上述控制方法[6−11]通过仿真实验说明方法的有效性.

我国赤铁矿不仅品位低而且具有嵌布粒度细且粒度分布不均等特点,需要两段闭路磨矿才能获得粒度合格的矿浆.由于一段磨矿矿浆流量波动大和再磨不合格矿浆–排矿流量等随机干扰影响,导致泵池液位发生较大波动,如果采用液位定值闭环控制方法[4−11],会造成旋流器给矿压力较大波动,使给矿压力内环的闭环系统处于动态之中.文献[12]提出了泵池液位区间与给矿压力模糊切换控制,外环采用静态模型设定、模糊补偿器和切换机制组成的控制方法.由于再磨过程产生的不合格矿浆–排矿流量与给矿浓度相关,给矿浓度波动引起排矿流量波动,为了提高再磨过程控制系统的动态性能,文献[13]在文献[12]基础上设计了消除给矿浓度波动的区间智能控制器.当赤铁矿的粒度分布大范围变化时,使一段磨矿与磁选矿浆流量和再磨排矿流量频繁波动,导致给矿压力内环控制器设定值频繁波动,使给矿压力内环闭环控制系统处于动态之中.由于上述控制方法[12−13]的外环控制器设计没有考虑内环闭环控制系统的动态特性,基于规则的切换机制难以给出合适的给矿压力控制器的设定值,难以建立控制系统的稳定性和收敛性分析,因此,难以将泵池液位和给矿压力变化率在运行时间内控制在目标值范围内.

本文将上述随机干扰造成的动态特性未知变化用未建模动态来描述,设计了基于消除前一时刻未建模动态补偿信号的PI控制器,采用一步最优前馈控制律和提升技术,提出了泵池液位和给矿压力双速率区间控制算法,给出了所提算法的稳定性和收敛性分析,采用工业现场实际数据的半实物仿真实验,结果表明了所提算法的有效性.

1 控制问题描述

1.1 赤铁矿再磨过程简介

赤铁矿再磨过程的结构图如图1所示.由磁选机、球磨机、水力旋流器、泵池、泵池补加水阀门、矿浆泵和污水池、污水泵、冲洗水阀门等组成.再磨生产过程的来料为一段磨矿和磁选产生的矿浆,最终产品为旋流器溢流矿浆.

一段磨矿矿浆和磁选矿浆以流量q1(t)进入到泵池,通过控制泵池补加水阀门开度u1(t)使得进入旋流器的矿浆浓度DH(t)达到工艺规定的目标值,稀释后的矿浆在矿浆泵作用下以一定的给矿压力y1(t)输送给旋流器,在离心力的作用下分级出粒度合格的溢流矿浆,粒度不合格的矿浆则形成沉砂返回球磨机进行再磨,球磨机排矿以流量q2(t)进入到泵池,并和一段磨矿与磁选矿浆流量q1(t)、不定期工作的污水与冲洗水流量q3(t)以及泵池补加水流量q4(t)充分混合后在泵池矿浆泵的输送下,以一定的频率u(t)从泵池抽出,从而维持泵池液位y2(t)在工艺要求的安全范围内.

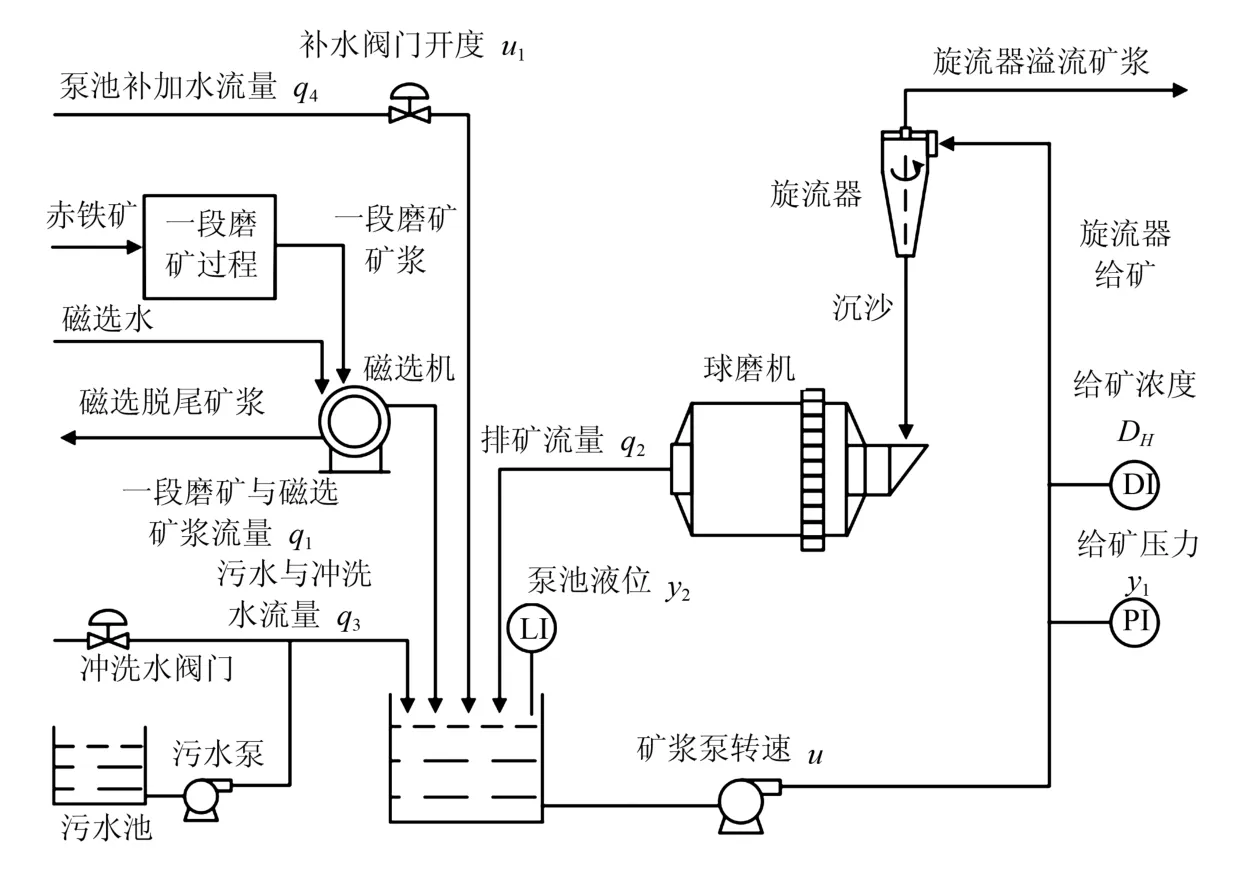
图1 赤铁矿再磨过程结构图Fig.1 Hematite regrinding process structure diagram

1.2 赤铁矿再磨过程动态模型分析

根据文献[14],以矿浆泵频率u(t)为输入,以泵池液位y2(t)为输出的动态模型为

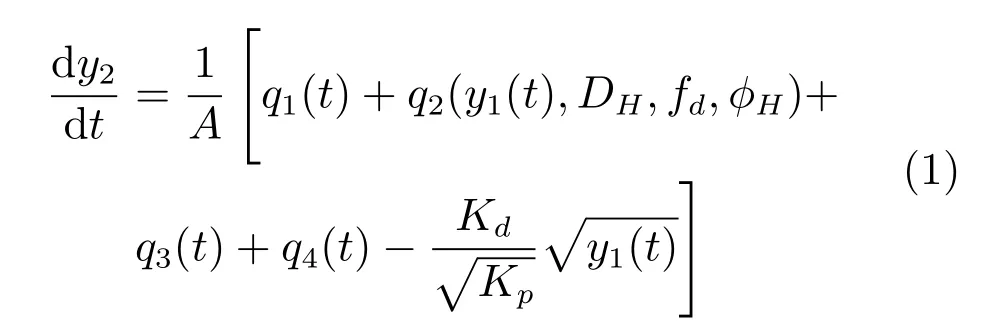
式中,给矿压力y1(t)表示为[15−16]:

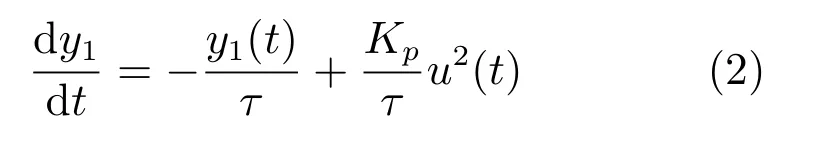
式(1)和式(2)模型参数描述,如表1所示.

表1 模型参数表Table 1 Model parameters

由式(1)和式(2)可知,再磨过程的泵池液位和给矿压力是以矿浆泵频率u(t)为输入,以给矿压力y1(t)为内环输出,以泵池液位y2(t)为外环输出的强非线性串级过程.其中,再磨过程不合格矿浆–排矿流量q2(y1(t),DH,fd,ϕH)是与旋流器给矿浓度DH(t)、给矿压力y1(t)、旋流器给矿粒度分布fd(t)和旋流器结构参数ϕH相关的未知非线性函数.当赤铁矿粒度分布大范围变化时,使旋流器给矿浓度DH(t)和粒度分布fd(t)发生波动,造成q2(y1(t),DH,fd,ϕH)波动,同时一段磨矿与磁选矿浆流量q1(t)和污水与冲洗水流量q4(t)的干扰,使矿浆液位频繁波动,导致给矿压力控制器设定值波动,使给矿压力内环闭环控制系统处于动态之中,泵池液位外环和给矿压力内环相互影响,为了消除未建模动态变化的影响,利用再磨过程运行在工作点附近的特点,将式(1)和式(2)在工作点处线性化可得:

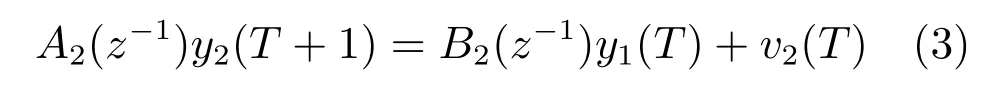
式中,A2(z−1)=1+a21z−1,B2(z−1)=b20.

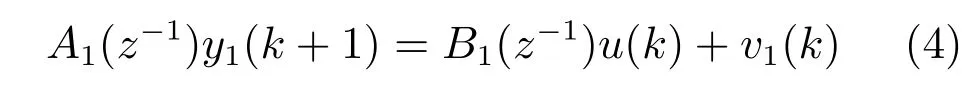
式中,A1(z−1)=1+a11z−1,B1(z−1)=b10.

泵池液位y2(T)和给矿压力y1(k)具有不同的时间尺度,其中,泵池液位采样周期为T,给矿压力采样周期为k.利用输入输出数据通过实验确定A2(z−1)、B2(z−1)、A1(z−1)和B1(z−1)的阶次和参数,未建模动态v2(T)和v1(k)为高阶非线性项,且v2(T)和v1(k)有界,即:|v2(T)|≤N;|v1(k)|≤M.

再磨过程的控制目标是:在所有运行时间内,满足矿浆泵的约束下,即:umin≤u(k)≤umax,将泵池液位y2(T)和给矿压力变化率∆y1(k)控制在目标值范围内,即:

其中,y2sp(T)为泵池液位的目标值,δ1为泵池液位波动幅度的上限值;δ2为给矿压力波动的上限值.

2 泵池液位和给矿压力双速率区间控制方法

由于泵池液位和给矿压力是串级过程,因此首先设计给矿压力内环控制器.为了克服给矿压力内环闭环系统动态波动对泵池液位外环的影响,采用提升技术[17],将给矿压力内环闭环控制系统的动态特性引入到泵池液位模型式(3),得到以给矿压力设定值y1(T)为输入,以泵池液位y2(T)为输出的采样周期为外环采样周期的动态模型,以此模型设计泵池液位外环控制器,从而实时产生给矿压力内环控制的设定值y1sp(T),通过给矿压力内环控制器,使给矿压力y1(T)跟踪设定值y1sp(T),实现对泵池液位的控制.

q1(t)、q2(t)、q3(t)和q4(t)的波动引起的泵池液位和给矿压力的特性变化,由未建模动态v2(T)和v1(k)表示.由于v2(T)和v1(k)始终处于动态波动之中,导致控制器积分作用失效,因此必须设计消除v2(T)和v1(k)影响的控制器.虽然未建模动态v2(T)和v1(k)未知,但是v2(T)和v1(k)可以表示为v2(T)=v2(T−1)+∆v2(T)和v1(k)=v1(k−1)+∆v1(k).因此利用前一时刻的未建模动态,设计消除前一时刻未建模动态v2(T−1)和v1(k−1)的影响的补偿信号,叠加到基于确定线性模型设计的反馈控制器,使闭环系统跟踪误差变小,将泵池液位和给矿压力变化率在运行时间内控制在目标值范围内.

被控对象模型式(3)和式(4)可以表示为

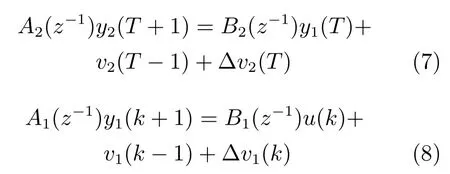
由式(7)和式(8)可得v2(T−1)和v1(k−1),

式(11)和式(12)为泵池液位和给矿压力的控制器驱动模型[18]的输出.采用式(9)～(12)可以求得v2(T−1)和v1(k−1),同时该方法在考虑当一段磨矿与磁选矿浆流量和再磨排矿流量频繁波动的基础上,采用一步最优前馈补偿律设计PI控制器,以此设计未建模动态补偿的PI控制器.

本文提出的双速率区间控制结构图如图2所示.给矿压力内环控制器和泵池液位外环控制器设计如下.

2.1 未建模动态补偿的给矿压力PI控制器

基于未建模动态补偿的给矿压力PI控制器的结构如图3所示,其中,u1(k)为基于给矿压力模型式(4)中的确定线性部分模型设计PI控制器输出,u2(k)为前一时刻未建模动态v1(k−1)补偿器的输出,即

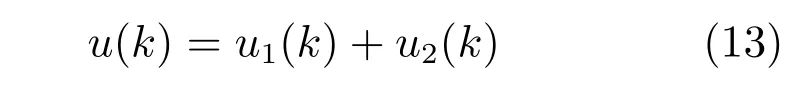
以式(8)的确定线性部分模型设计的PI控制器为

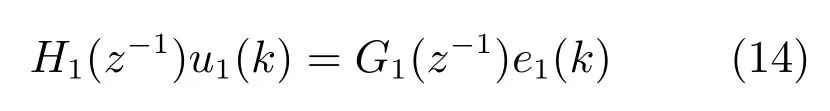
式中,H1(z−1)=1−z−1、G1(z−1)=g10−g11z−1,g10和g11为PI控制参数,e1(k)为跟踪误差,即:e1(k)=y1sp(k)−y1(k).

未建模动态v1(k−1)补偿器为

式中,K1(z−1)为补偿器的参数.

采用一步最优前馈补偿律来设计G1(z−1)和K1(z−1)的参数,将式(14)中的u1(k)和式(15)中的u2(k)代入式(13)中得到u(k)为

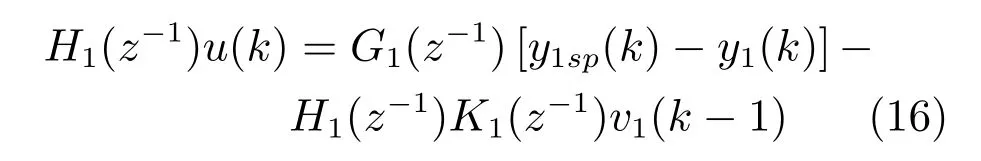
引入下列性能指标[19]:

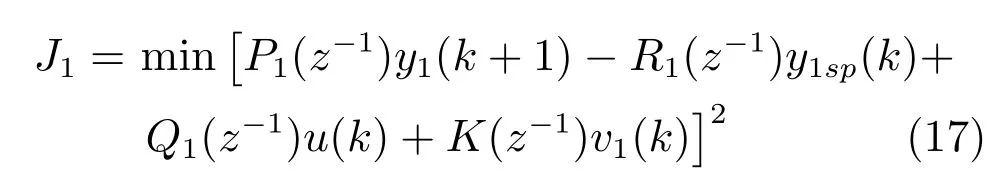
式中,P1(z−1)、R1(z−1)、Q1(z−1) 和K(z−1)均为关于z−1的加权多项式.

引入广义输出ϕ1(k+1)为

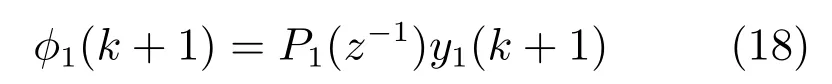
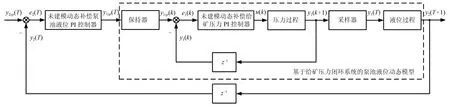
图2 泵池液位和给矿压力双速率区间控制结构图Fig.2 The structure of the dual rate interval control of the pump pool level and feeding pressure

图3 未建模动态补偿给矿压力PI控制结构图Fig.3 PI control structure for dynamic compensation of the feeding pressure

定义式(17)中的P1(z−1)为

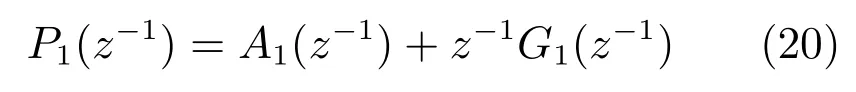
由式(8)和式(20)可得

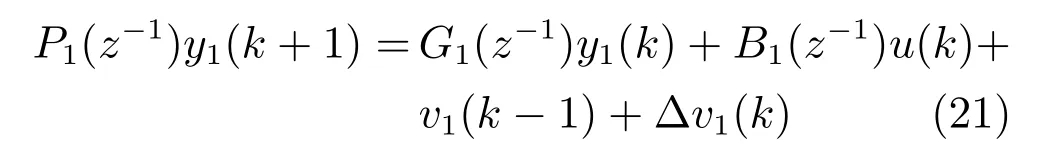
将式(21)代入式(17)中,使Jmin=∆v1(k)可得带有未建模动态补偿的一步最优控制律为

由式 (16)和式 (22)可得Q1(z−1)、R1(z−1)、K(z−1)为

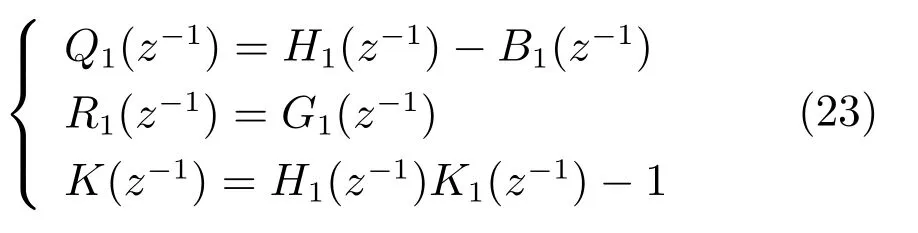
将式(22)和式(23)代入到给矿压力被控对象式(8)中得到给矿压力闭环系统方程为

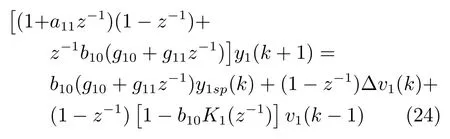
选择g10和g11满足:

由式(24)可知,为实现对v1(k−1)的动态和静态补偿,选择K1(z−1)使1−b10K1(z−1)=0,即:

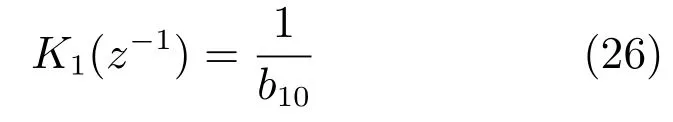
未建模动态补偿的给矿压力PI控制器输出u(k)可以由式(13)求得,其中,u1(k)由式(14)和式(25)求得,u2(k)由式(15)和式(26)求得.

2.2 未建模动态补偿的泵池液位PI控制算法

将式(16)代入式(8)中,得到给矿压力闭环控制系统为

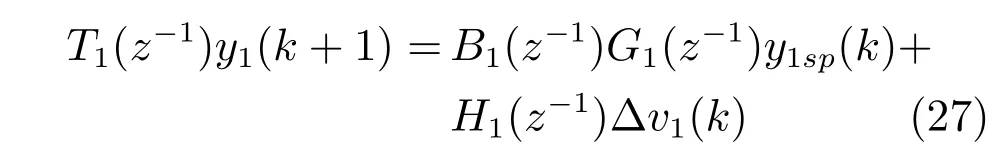
式中,T1(z−1)=(1+a11z−1)(1−z−1)+z−1b10(g10+g11z−1)=1+t1z−1+t2z−2

一段磨矿与磁选矿浆流量和再磨排矿流量频繁波动,导致泵池液位y2(T)发生频繁波动,造成给矿压力内环控制器设定值y1sp(T)波动,给矿压力闭环控制系统式(27)处于动态之中,泵池液位外环控制器设计需要建立基于给矿压力内环闭环控制系统特性的泵池液位外环动态模型,采用提升技术[19]将式(27)转化为状态方程形式,选择状态变量:x1(k)=−t2y1(k−1)+b10g11y1sp(k−1)−∆v1(k−1)、x2(k)=y1(k).将式(27)表示为

由式(28)可得:

当i=0,1,2,···,4时,将式(29)进行迭代,可得:

利用零阶保持器,使

其中i=0,1,2···,4.

由T=5k,状态方程式(28)和式(29)中的输出方程分别转化为

将式(32)和式(33)转换成输入输出的形式,即:

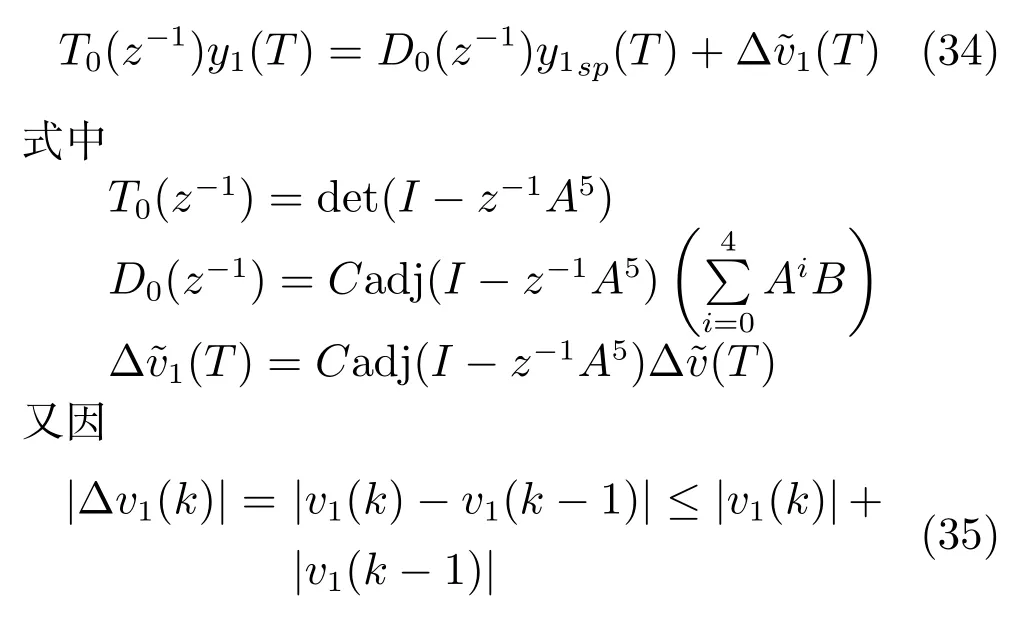
由|v1(k)|≤M和式(35)可得:

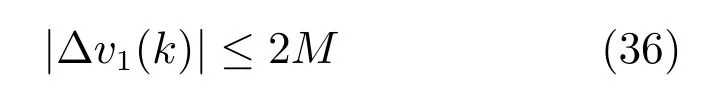
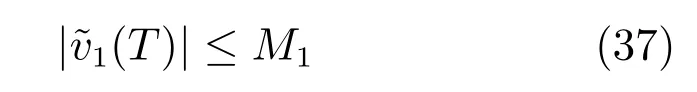
式中,M1为的上界.

将式(34)代入式(3)中,得到以给矿压力设定值y1sp(T)为输入,以泵池液位y2(T+1)为输出的动态模型,即:

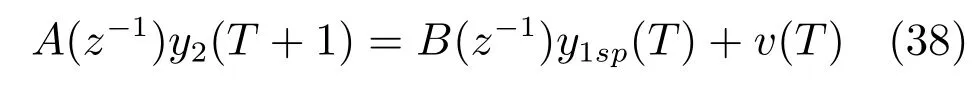
式中

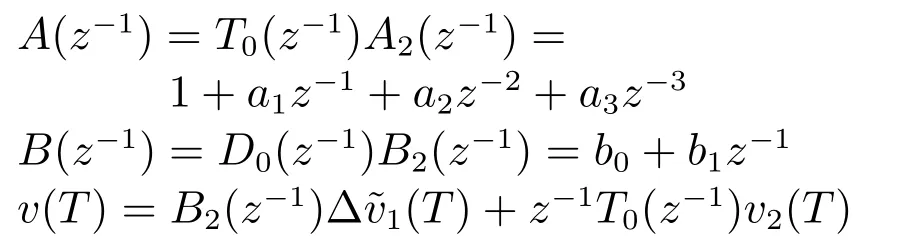
v(T)由给矿压力内环未建模动态变化率∆v1(k)和泵池液位外环未建模动态v2(T)组成.由v2(T)和v1(k)有界,可知v(T)有界,即:|v(T)|≤W.因此通过设计对v(T−1)的补偿信号,消除v(T−1)对泵池液位y2(T)的影响.

采用未建模动态补偿的给矿压力PI控制器的设计方法,设计泵池液位控制器,其输出y1sp(T)为

y1sp1(T)为确定线性部分模型设计的PI控制器输出,即:

式中,H2(z−1)=1−z−1、G2(z−1)=g20+g21(z−1),g20和g21为PI控制器参数、e2(T)为跟踪误差,e2(T)=y2sp(T)−y2(T).

y1sp2(T)为v(T−1)的补偿器输出,即:

式中,v(T−1)=A(z−1)y2(T)−B(z−1)y1sp(T−1).

采用一步最优前馈补偿律来设计G2(z−1)和K2(z−1)的参数,将式(40)中的y1sp1(T)和式(41)中的y1sp2(T)代入式(39)中得到y(T)为

将式(42)代入式(38)中得到泵池液位闭环系统方程为

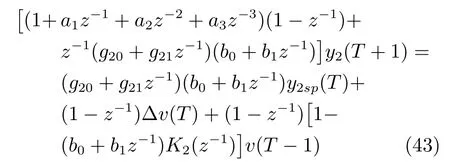
选择g20和g21使下式成立

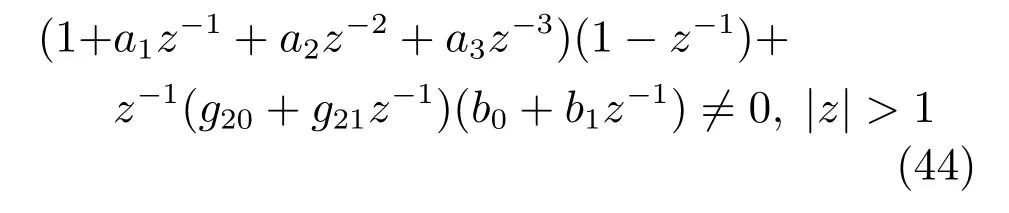
由B(z−1)稳定,根据式(43)可得未建模动态补偿参数K2(z−1)为1/(b0+b1z−1),将K2(z−1)代入式(42)可得:

其中,g20和g21通过凑式满足式(44).

3 稳定性和收敛性分析

为了证明本文所提出泵池液位和给矿压力双速率串级控制方法可以使闭环系统具有稳定性和收敛性,引入引理.

引理1.当控制器式(42)作用于被控对象式(38)时,系统的输入输出方程可以由式(46)和式(47)表示.

证明.将式(42)代入式(38),可以证明泵池液位输入输出方程式(46)成立.将式(46)代入式(38)可以证明泵池液位输入输出方程式(47)成立.□

定理 1.被控对象由式 (7)～(10)表示,当T→∞时,未建模动态变化率∆v1(∞)和∆v2(∞)为常数.若采用控制律式(16)和式(42),则被控对象的闭环系统的输入输出信号一致有界(BIBO(Bounded input bounded)稳定),即

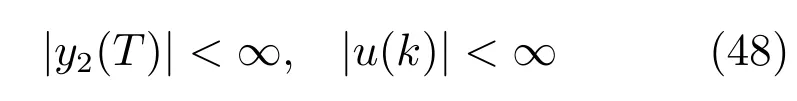
并且,被控对象的输出y2(T)和y1(k)与参考输入y2sp(T)和y1sp(k)之间的稳态误差小于预先设定值ε2和ε1,即

证明.因为

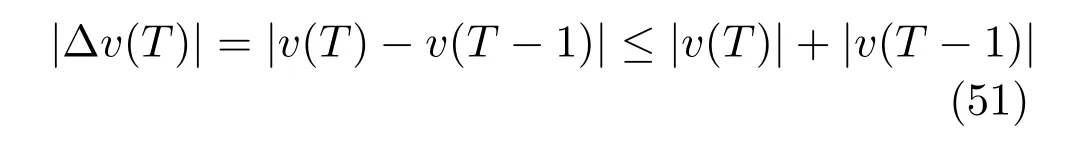
由式(51)和v(T)有界可得∆v(T)有界,即

由式 (46)和式 (47)可知,y2sp(T)、v(T)和∆v(T)有界,采用文献[20]类似方法可证:

其中,c1、c2、c3和c4为正常数.

由式(16)作用于被控对象式(8)可得给矿压力的输入输出方程,由式(27)和式(55)表示.

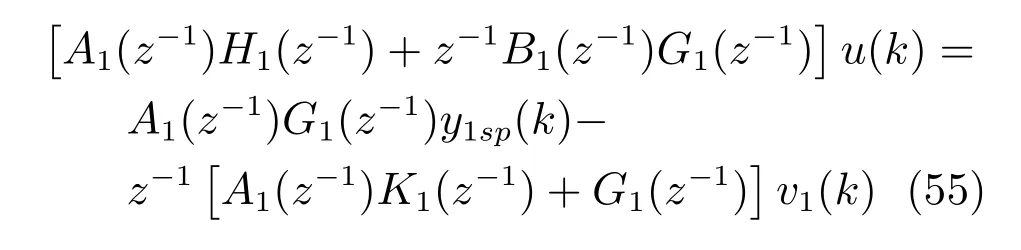
由式(27)和式 (55)可知,y1sp(k)、v1(k)和∆v1(k)有界,采用文献[20]类似方法可证:

其中,d1、d2、d3和d4为正常数.

由式(57)和式(53)可知闭环系统的输入u(k)和输出y2(T)均有界.

由式(46),当T→∞时,泵池液位的稳态跟踪误差e2(T)为

当T→∞时,由于∆v1(∞)和∆v2(∞)为常数,根据式(37)和式(38),∆v(∞)为常数,得:

由式(27),当k→∞时,给矿压力的稳态跟踪误差e1(k)为

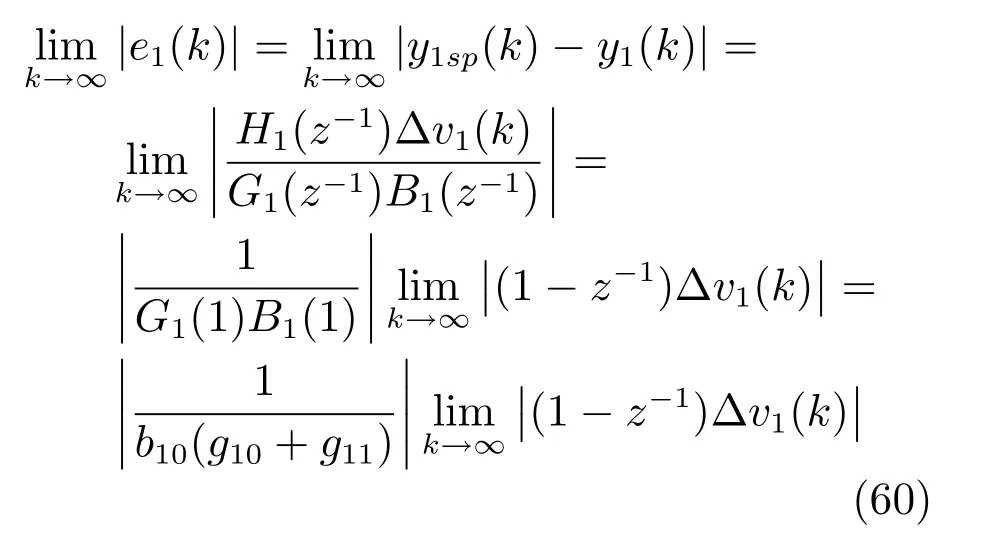
4 再磨过程半实物仿真系统实验

当k→∞时,由于∆v1(∞)为常数,得:

将本文提出的再磨过程的泵池液位和给矿压力双速率区间控制方法在再磨过程的半实物平台进行实验研究,以验证其有效性和实用性.

4.1 半实物仿真的软硬件平台

为了说明本文提出的双速率区间控制方法的有效性,研发了赤铁矿再磨过程的半实物仿真实验系统.硬件平台由对象计算机、监控计算机、控制器设计计算机、控制系统和虚拟仪表及执行机构组成,如图4所示.

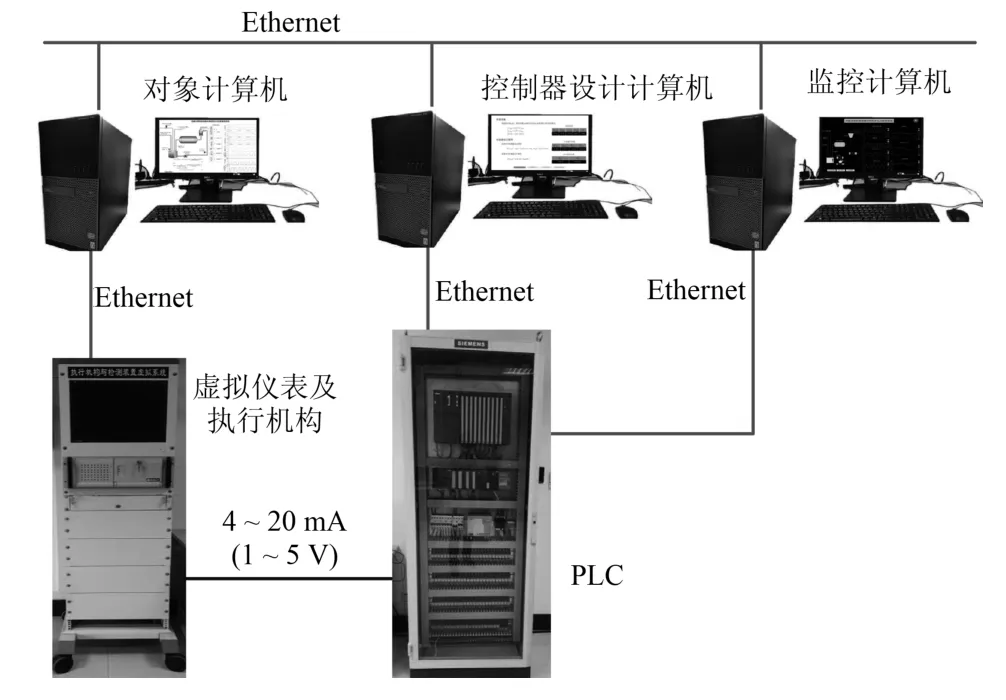
图4 赤铁矿再磨过程半实物仿真系统硬件平台Fig.4 Hematite regrinding process of semi physical simulation system of hardware platform

软件平台主要由Matlab、控制系统软件、OPCScout软件和相关系统软件组成,主要实现系统的整体设计、可视化人机界面设计、被控对象模型设计、控制器设计和系统之间的实时通讯等功能,如图5～7所示.

4.2 被控对象仿真模型

采用欧拉法将式(1)和式(2)进行离散化为

由于式(62)中的Qin(T)/A和未知,采用未知常数F和K0代替,得到式(62)的近似模型:

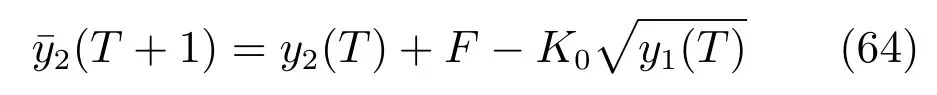
未建模动态∆y2(T)可以表示为

由式(64)和式(65)得到泵池液位辨识方程为

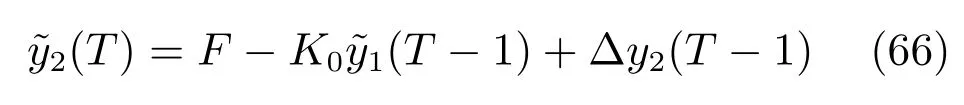
采用工业过程实际的给矿压力和泵池液位数据,采用文献[21]的交替辨识算法获得式(66)中F和K0的估计值为和未建模动态∆y2(T)的估计值为泵池液位仿真模型为

采用工业过程实际的矿浆泵频率和给矿压力数据,采用最小二乘辨识方法估计式(63)中模型参数,可得给矿压力仿真模型为

将式(67)和式(68)作为半实物仿真系统的被控对象模型.

4.3 控制目标及控制器参数选择

工艺要求在矿浆泵频率约束30≤u(k)≤45 Hz前提下,泵池液位的控制目标范围为

给矿压力工艺要求的最大波动范围为±6 kPa,可以表示为

根据泵池区间液位控制目标范围,确定泵池液位的参考值为y2ref=(1.3+0.3)/2=0.8m.

泵池液位和给矿压力控制器设计模型参数为

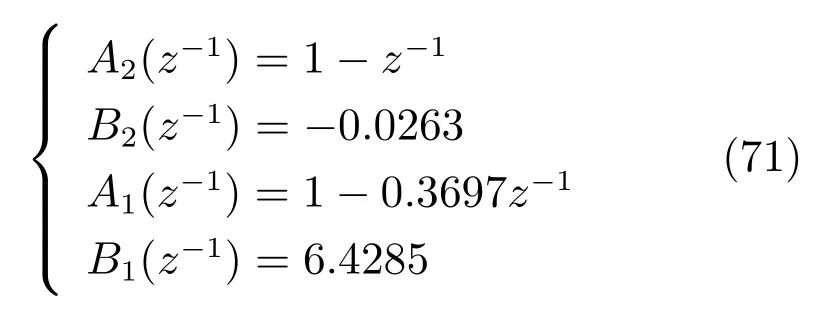
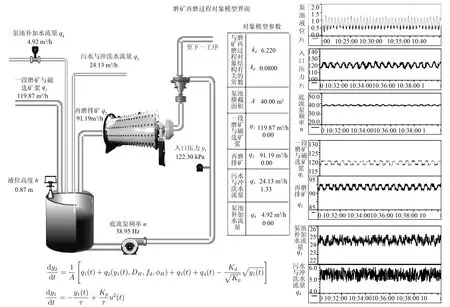
图5 被控对象设计界面Fig.5 The design interface of the controlled object

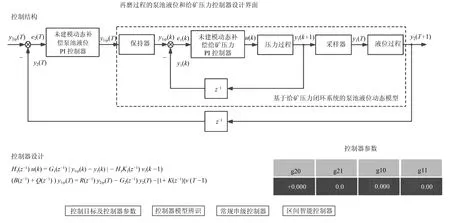
图6 控制器设计界面Fig.6 The design interface of the controller

由式(25)和式(26)确定基于未建模动态补偿的给矿压力回路控制的参数为

由式(38)确定基于提升技术给矿压力内环闭环控制系统的动态特性引入到泵池液位控制器设计模型参数为

由式(44)和式(45)确定基于未建模动态补偿的泵池液位回路控制的参数为

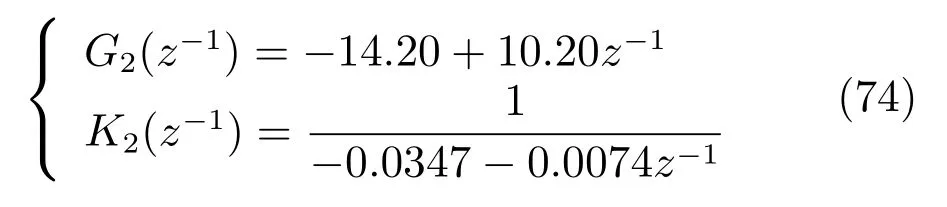
泵池液位区间控制和给矿压力回路控制组成的模糊切换控制方法的控制参数与文献[12]中的参数相同.

串级PI控制参数与本文的PI控制参数相同.

4.4 实验研究

为了验证本文提出的控制算法的动态性能,在相同的频繁干扰下,将本文所提控制方法、文献[12]所提控制方法以及串级PI控制方法进行半实物仿真对比实验.在21:31:50～21:36:50时间内,Qin(t)在[227m3/h,253m3/h]内频繁波动.在21:36:50～21:41:50时间内,Qin(t)在[117m3/h,263m3/h]内频繁波动,波动曲线如图8所示.

采用被控对象式(67)和式(68)作为半实物仿真对象,对比仿真实验结果如图9～12所示.

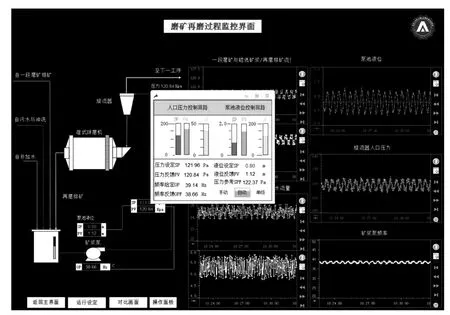
图7 监控设计界面Fig.7 The design interface of the monitor

图8 Qin波动运行曲线Fig.8 The fluctuation curve of Qin

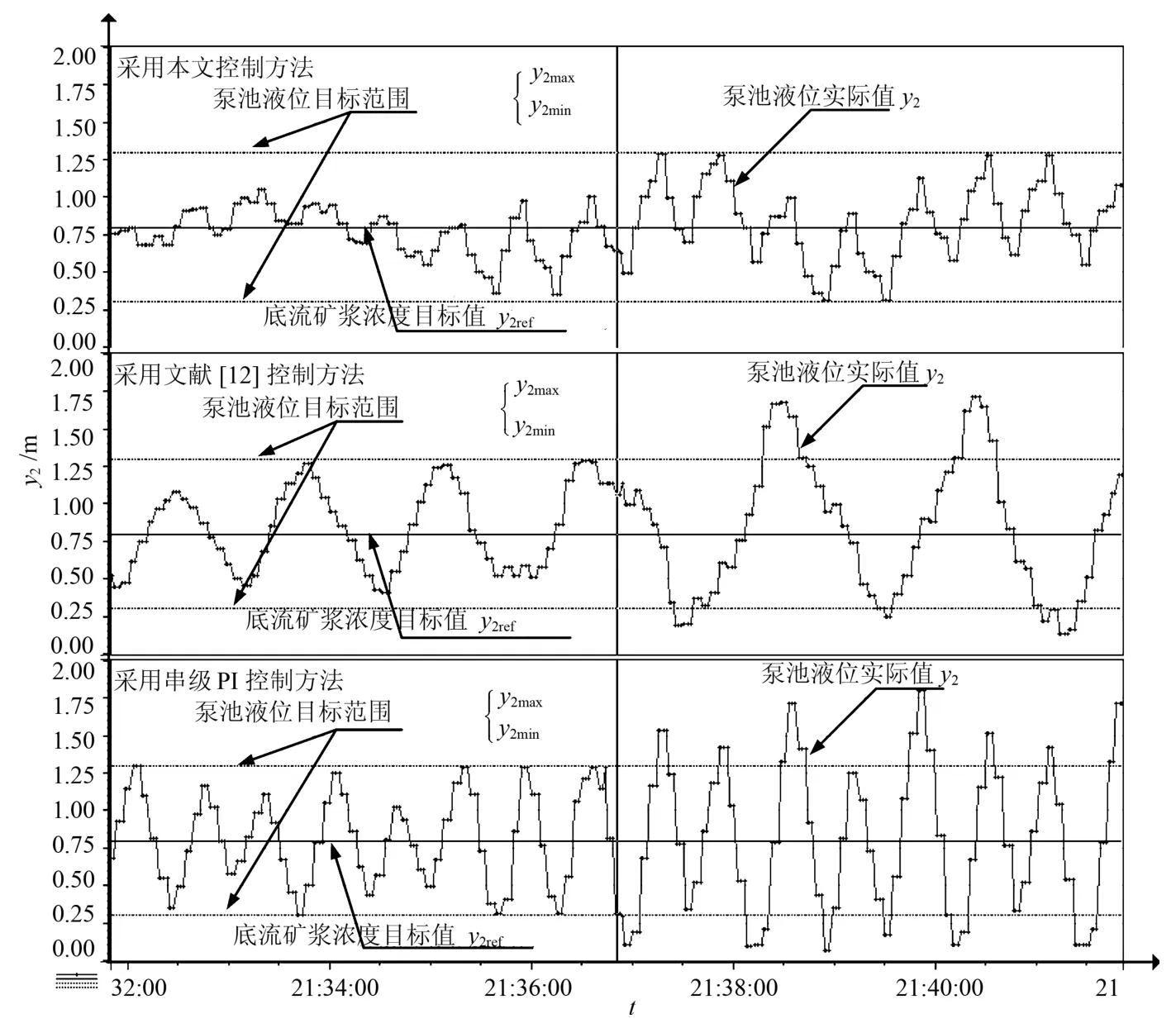
图9 泵池液位实际值y2运行曲线Fig.9 The curve of actual value of the level of pump pool y2

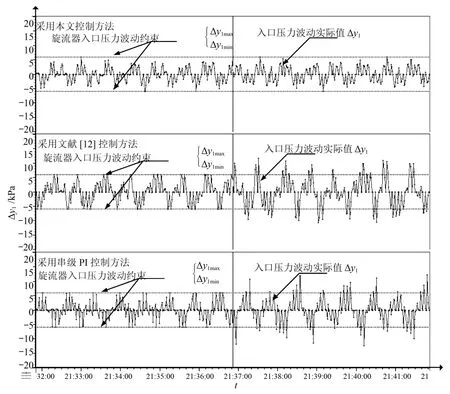
图11 给矿压力变化率∆y1运行曲线Fig.11 The operation curve of feeding pressure ratio∆y1

图12 矿浆泵频率的实际值u运行曲线Fig.12 The curve of actual value of slurry pump speed u

从图9～12中分析可知,在21:31:50～21:41:50时间内,采用本文提出的控制方法可以将泵池液位和给矿压力的波动控制在式(69)和式(70)的目标范围内.但是明显可以看出采用文献[12]提出的控制方法和串级PI控制方法在21:31:50～21:36:50时间内,可以将泵池液位控制在式(69)目标范围内;但是在21:36:50～21:41:50时间内,使泵池液位超出式(69)的目标范围,同时也造成旋流器的给矿压力波动超出式(70)的目标范围.以下是将上述三种控制器进行性能比较,如表2和表3所示.

表2 采用本文控制方法、文献[12]控制方法和串级PI控制方法时泵池液位y2的性能评价Table 2 The performance evaluation of the level of pump pool by y2using the control method,the[12]control method and the cascade PI control method

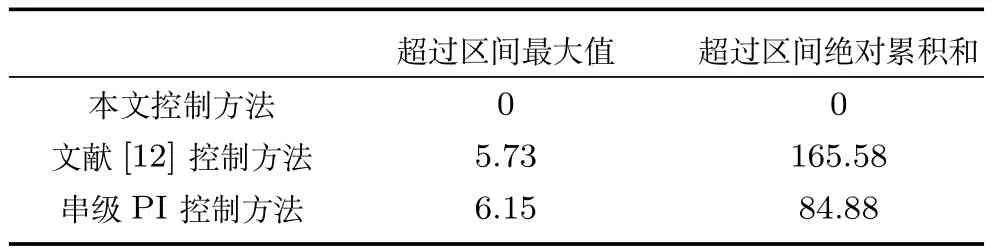
表3 采用本文控制方法、文献[12]控制方法和串级PI控制方法时给矿压力变化率∆y1的性能评价Table 3 the performance evaluation of the feeding pressure ratio∆y1by using the control method,the[12]control method and the cascade PI control method

由上表可以分析出,在21:31:50～21:41:50时间内,采用本文控制方法对式(67)和式(68)的被控对象进行控制时,使泵池液位y2和给矿压力变化率∆y1控制在工艺要求目标区间内.在21:31:50～21:41:50时间内,采用文献[12]控制方法对式(67)和式(68)的被控对象进行控制时,泵池液位y2超过被控对象的控制目标式(69)的区间最大值为0.42,超过该目标区间的绝对累积和为15.62;旋流器的给矿压力变化率∆y1超过被控对象的控制目标式(70)的区间最大值为5.73,超过该目标区间的绝对累积和为165.58.在21:31:50～21:41:50时间内,采用串级PI控制方法对式(67)和式(68)的被控对象进行控制时,泵池液位y2超过被控对象的控制目标式(69)的区间最大值为0.50,超过该目标区间的绝对累积和为22.92;旋流器的给矿压力变化率∆y1超过被控对象的控制目标式(70)的区间最大值为6.15,超过该目标区间的绝对累积和为84.88.半实物仿真结果表明,本文方法在受到大范围随机干扰时,不需要文献[12]基于规则的切换机制,可将泵池液位y2和给矿压力变化率∆y1控制在工艺规定的范围内.

5 结论

本文提出的再磨过程双速率区间控制由内环未建模动态补偿给矿压力PI控制器和基于给矿压力内环闭环控制系统动态特性的泵池液位外环动态模型设计的未建模动态补偿PI控制器组成,采用一步最优前馈补偿律设计补偿器和PI控制器的参数.稳定性与收敛性分析和半实物仿真实验结果表明,再磨过程受到频繁随机干扰时,所提出的控制方法可将泵池液位和给矿压力变化率控制在目标值范围内.本文所提的双速率区间控制器设计方法对受到大范围随机干扰的非线性串级工业过程的控制器设计具有参考价值.

1 Li X,McKee D J,Horberry T,Powell M S.The control room operator:the forgotten element in mineral process control.Minerals Engineering,2011,24(8):894−902

2 van Vuuren M J J,Aldrich C,Auret L.Detecting changes in the operational states of hydrocyclones.Minerals Engineering,2011,24(14):1532−1544

3 Wei D H,Craig I K.Grinding mill circuits—a survey of control and economic concerns.International Journal of Mineral Processing,2009,90(1−4):55−56

4 Duarte M,Sepúlveda F,Castillo A,Contreras A,Lazcano V,Gimnez P,Castelli L.A comparative experimental study of five multivariable control strategies applied to a grinding plant.Powder Technology,1999,104(1):1−28

5 Chu Yun-Fei,Xu Wen-Li,Wang Jun,Wan Wei-Han.Averaging level control based on switching control.Journal of Tsinghua University(Science and Technology),2005,45(1):107−110(楚云飞,徐文立,王峻,万维汉.基于切换控制的均匀液位控制.清华大学学报(自然科学版),2005,45(1):107−110)

6 Pomerleau A,Hodouin D,Desbiens A,Gagnon É.A survey of grinding circuit control methods:from decentralized PID controllers to multivariable predictive controllers.Powder Technology,2000,108(2−3):103−115

7 Liang Lei,Li Zhen-Guo.Fuzzy-intelligent control arithmetic for the ore pulp level in mineral separation process.Metal Mine,2009,39(7):103−105,135(梁蕾,李振国.选矿过程矿浆液位的模糊控制算法研究.金属矿山,2009,39(7):103−105,135)

8 Aguila-Camacho N,Le Roux J D,Duarte-Mermoud M A,OrchardM E.Control of a grinding mill circuit using fractional order controllers.Journal of Process Control,2017,53:80−94

9 le Roux J D,Padhi R,Craig I K.Optimal control of grinding mill circuit using model predictive static programming:a new nonlinear MPC paradigm.Journal of Process Control,2014,24(12):29−40

10 Coetzee L C,Craig I K,Kerrigan E C.Robust nonlinear model predictive control of a run-of-mine ore milling circuit.IEEE Transactions on Control Systems Technology,2010,18(1):222−229

11 Matthews B,Craig I K.Demand side management of a runof-mine ore milling circuit.Control Engineering Practice,2013,21(6):759−768

12 Zhao Da-Yong,Chai Tian-You.Fuzzy switching control for sump level interval and hydrocyclone pressure in regrinding process.Acta Automatica Sinica,2013,39(5):556−564(赵大勇,柴天佑.再磨过程泵池液位区间与给矿压力模糊切换控制.自动化学报,2013,39(5):556−564)

13 Zhao D Y,Chai T Y,Wang H,Fu J.Hybrid intelligent control for regrinding process in hematite bene ficiation.Control Engineering Practice,2014,22:217−230

14 Sanchis R,Romero J A,Martn J M.A new approach to averaging level control.Control Engineering Practice,2011,19(9):1037−1043

15 Wang Ze-Hong,Chen Xiao-Long,Yuan Zhi-Tao,Yu Fu-Jia,Li Li-Xia.Mathematical Model of Mineral Processing.Beijing:Metallurgical Industry Press,2015.(王泽红,陈晓龙,袁致涛,于福家,李丽匣.选矿数学模型.北京:冶金工业出版社,2015.)

16 Wu Xue-Juan,Lang Lang.Fuzzy Adaptive control of constant pressure water supplying system with frequency conversion.Industrial Control Computer,2010,23(11):53−54(吴学娟,郎朗.模糊自适应控制在变频恒压供水系统中的应用.工业控制计算机,2010,23(11):53−54)

17 Liu F Z,Gao H J,Qiu J B,Yin S,Fan J L,Chai T Y.Networked multirate output feedback control for setpoints compensation and its application to rougher flotation process.IEEE Transactions on Industrial Electronics,2014,61(1):460−468

18 Chai T Y,Zhang Y J,Wang H,Su C Y,Sun J.Data-based virtual unmodeled dynamics driven multivariable nonlinear adaptive switching control.IEEE Transactions on Neural Networks,2011,22(12):2154−2172

19 Jia Y,Chai T Y.A data-driven dual-rate control method for a heat exchanging process.IEEE Transactions on Industrial Electronics,2017,64(5):4158−4168

20 Chai T Y,Zhai L F,Yue H.Multiple models and neural networks based decoupling control of ball mill coal-pulverizing systems.Journal of Process Control,2011,21(3):351−366

21 Zhang Y J,Chai T Y,Wang D H.An alternating identi fication algorithm for a class of nonlinear dynamical systems.IEEE Transactions on Neural Networks and Learning Systems,2016,PP(99):1−12