双绕组定子永磁型无轴承电机设计
2017-03-09贾红云袁安富曹永娟
李 权,贾红云,徐 放,袁安富,曹永娟
(南京信息工程大学,南京 210044)
双绕组定子永磁型无轴承电机设计
李 权,贾红云,徐 放,袁安富,曹永娟
(南京信息工程大学,南京 210044)
提出了一种12/8极双绕组定子永磁型无轴承电机,分析了其结构与径向悬浮力产生原理,推导了电机的功率方程,确定了电机的定子内径与轴长。从电机的等效磁路入手对定转子极弧和永磁体尺寸进行了计算。初步确定了电机的主要尺寸参数,用有限元法(FEM)对该尺寸电机的悬浮特性和转矩特性进行了计算和分析,计算结果验证了设计方法和理论分析的正确性。
定子永磁型;无轴承;径向悬浮力;功率方程;磁路
0 引 言
随着现代工业的发展,对高速和超高速电机有着迫切需求的领域不断增加[1-7]。然而传统电机因转子需要机械轴承支撑,运行时存在着磨损和振动等问题,限制了其转速的提升。磁轴承电机利用磁悬浮技术将电机转子悬浮,使电机转子与本体没有任何机械接触,有效的提升了电机的最高转速。但由于磁轴承电机是在传统电机的基础上增加一套磁悬浮装置,大大增加电机的体积、功耗与制造成本,难以在工程应用中得到推广。因此为了解决上述问题,将磁轴承技术和传统旋转电机相结合的无轴承电机在高速超高速的电机驱动系统中得到了广泛应用[1]。
目前,无轴承技术已被运用到多种类型的电机中[2-7]。其中无轴承永磁同步电机以其体积小、效率/功率密度高等优势在诸多领域具有实用化优势,被认为是最具应用前景的无轴承电机之一[6-7]。然而传统永磁电机的永磁体置于转子,存在着散热条件差和最高转速低等固有缺陷[8]。近些年出现的定子永磁型电机将永磁体置于定子,一方面易于电机散热,另一方面大大简化转子结构,提升了转子机械强度,并提高了电机的最高转速[8-9]。考虑到上述问题,本文研究一种定子永磁型无轴承电机(Stator-Permanent Magnet Bearingless,简称SPMB)电机。
目前,SPMB电机的研究主要集中在电磁特性分析与数学模型的推导[10-11],而关于该电机的功率方程相关内容未见报道。本文的主要目的是探讨SPMB电机的功率尺寸方程,从等效磁路出发,计算电机主要参数的尺寸。
1 拓扑结构和悬浮力产生原理
1.1 拓扑结构
三相12/8极SPMB电机的结构如图1所示。定子齿A、定子齿B和定子齿C在空间相位上互差30°,定、转子均为双凸极结构,定子被均匀的分成4块,两两之间嵌有4块同极相对的永磁体,具有聚磁作用,以便获得较高的气隙磁密。在每一定子齿上分别使用两套绕组,一套为电枢绕组,另一套为悬浮绕组,且均为集中式绕组。且转子上既无永磁体也无绕组,适合长时间高速稳定运行。
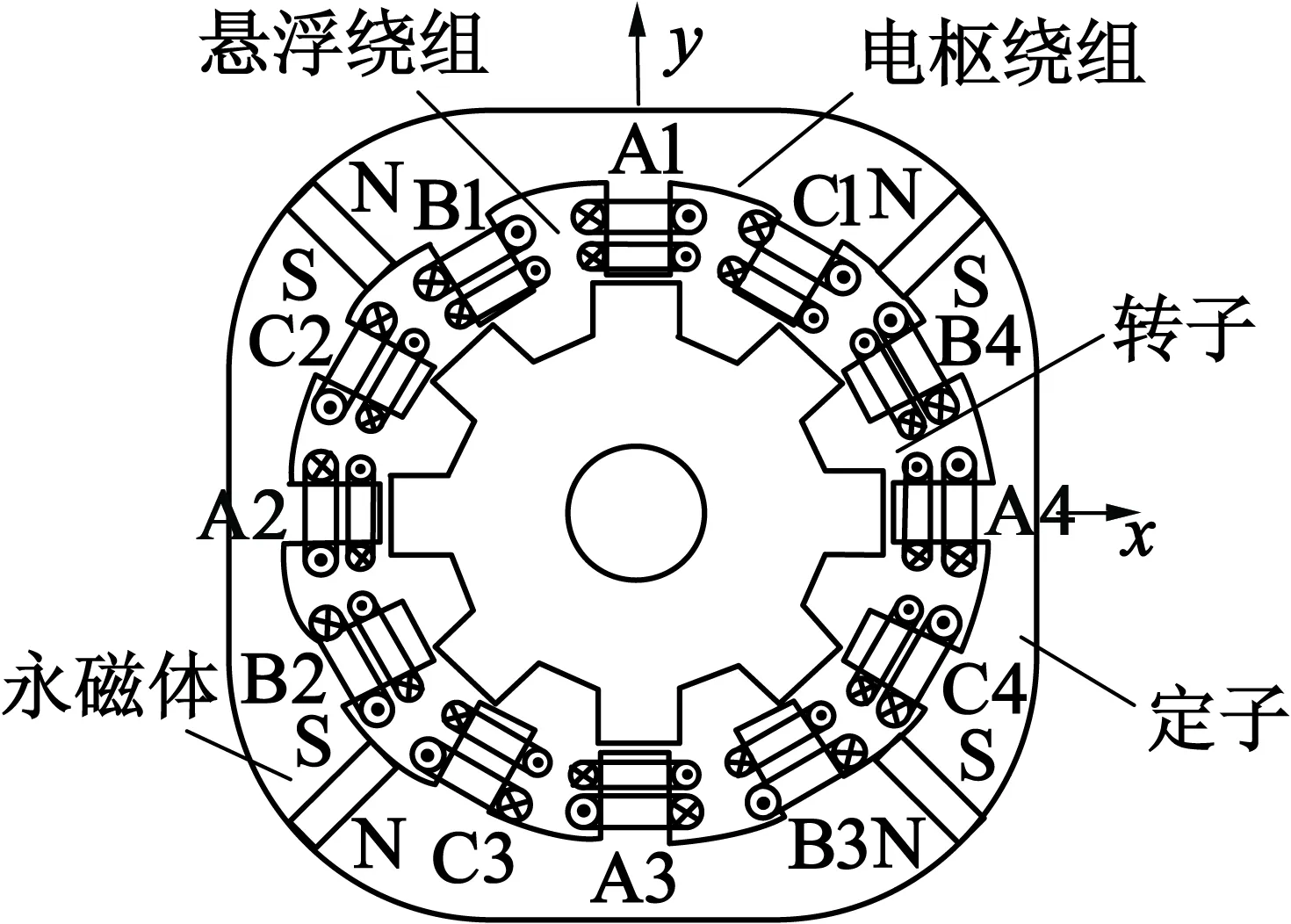
图1 SPMB电机拓扑结构
1.2 悬浮力产生原理
通常无轴承电机是在原来电机的基础上增加一套悬浮绕组,使电机即可产生切向力即转矩,又可产生可控径向力。通过悬浮绕组产生的磁场改变电机的原始气隙磁场分布,即某些地方磁密增强,与其对称处磁密减弱,从而产生由气隙磁密减弱方向指向气隙磁密增强方向的力。
空载情况下,电机转子在初始位置时,只对A2和A4齿下的悬浮绕组加载正向电流,悬浮磁链和永磁磁链的分布情况如图2所示。黑色虚线表示4块永磁体产生的永磁磁链,红色虚线表示A2和A4齿下的悬浮绕组产生的悬浮磁链。A4齿下的永磁磁链与悬浮磁链方向相同,而A2齿下的永磁磁链与悬浮磁链方向相反,使得A4齿处的气隙磁密增强,而A2齿处的气隙磁密减弱,从而产生由A2齿指向A4齿的力,即沿X轴正方向的径向悬浮力。
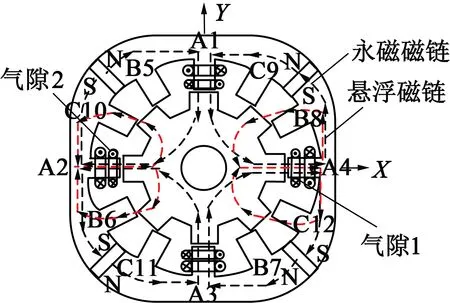
图2 径向悬浮力的原理
2 功率方程
无轴承电机在额定运行的工况下除了要稳定的输出电磁转矩,还根据不同径向负载和转子偏心情况输出径向悬浮力。因此无轴承电机的输入功率分为电枢绕组功率Parm和悬浮绕组功率Psus两部分,则输入功率P1可表示:
(1)
设SPMB电机电枢绕组和悬浮绕组分别施加的相电压为uarm和usus,电枢绕组相电流iarm幅值为Im的方波;悬浮绕组相电流isus是关于转子位置θr和偏心量α,β有关的函数,本文推导过程是在假设径向无偏移的情况下进行的,这里以方波表示,幅值为Is,如图3所示。则外部输入电机的电枢绕组功率Parm和悬浮绕组功率Psus分别为:
(2)
(3)
式中:T=θcr/ωr,ΔTm=θw/ωr,ΔTs=T/m;转子极弧θcr=2π/pr;正负半周通电区间θw=θ2-θ1=θ4-θ3;转子极数pr;电枢相电压有效值Um;相电流峰值Im;悬浮相电压有效值Us;相电流峰值Is;机械角速度ωr;与转子位置角θr对应的时间ti(i=1,2,3,4,5,6)。
由此,式(1)可以表示:
(4)
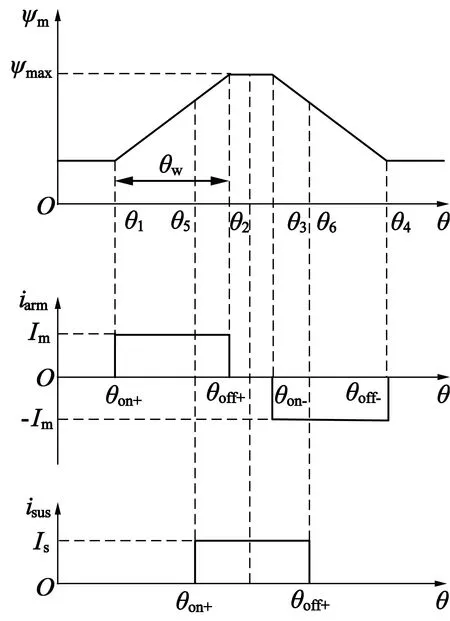
图3 电机磁链与电流理论波形
在这里假设悬浮绕组输入功率与电枢绕组输入功率比率km=Psus/Parm并代入式(4)可得:
(5)
定义电机效率为η,可以得到电机的输出功率P2:
(6)
由θcr=2π/pr,可得:
(7)
式(7),ke=U/E,E为永磁磁链在一相绕组中感应产生的空载反电势,并可表示:
(8)
由有限元仿真可以得出磁链的最大值和最小值分别是0.220 6 Wb和0.003 8 Wb,可得:
ΔΦ=0.220 6-0.003 8=0.182 6≈
(9)
式中:漏磁系数kd,定子极弧系数αs,定子极距τs=πDsi/ps,定子极数ps,永磁体所产生的气隙磁密峰值Bg_max,定子内径Dsi,有效轴长le。
由式(5)和(6)可以得到反电势E:
(10)
电枢绕组中电流Im的表达式:
(11)
式中:电流密度As,电流有效值Irms,ki=Im/Irms。
将式(7)和式(8)代入式(4)可得:
(12)
式中:ns为电机的额定转速。建立了SPMB电机的输出功率与电磁参数间的关系。
3 主要尺寸
由式(12)得到电机的主要尺寸与其输出功率之间的通用关系:
(13)
3.1 定子内径和轴长
式(13)中ke是电机电枢绕组相电压与空载反电势之比,取1.5。kd为漏磁系数,取0.9。电机的线负荷As取值15 000 A/m。km是悬浮绕组功率与电枢绕组功率之比,取0.316。电机空载时,气隙磁密峰值Bg_max取1.6 T。电机额定转速ns取1 500 r/min,电机效率为83%,对于输出功率为750 W的电机,可以计算得:
(14)
进而得到电机的定子内径和轴长分别:
(15)
3.2 定、转子极弧
由于SPMB电机定转子具有双凸极特性,通常要求无论转子处于何种位置都具有较小的磁导,因此定、转子极弧满足以下约束:
(16)
式中:βs,βr分别表示电机的定、转子极弧。此外,根据电机的双极性特性,定、转子极弧需要满足下述条件才能确保电流的正确换向。
(17)
分析前假设铁心磁导率无穷大,SPMB电机的等效磁路图如图4所示,永磁磁势、永磁磁阻以及其对应的漏磁磁阻分别为Fpm1~Fpm4,Rpm1~Rpm4和Rbm1~Rbm4;A,B,C三相定子齿极对应的气隙磁阻为Ra1~Ra4,Rb5~Rb8,Rc9~Rc12;A,B,C三相定子齿极对应的气隙磁通为Φa1~Φa4,Φb5~Φb8,Φc9~Φc12。

图4 SPMB电机等效磁路图
在求解SPMB电机的定转子极弧时可以做以下假设:
1) 转子不偏心α=β=0,那么可得每一相不同定转子齿之间的磁阻相等;
2) 令电枢电流iarm和悬浮电流isus均为0。
简化后的SPMB电机等效磁路图如图5所示,永磁磁势A,B,C三相总气隙磁阻分别为Ra,Rb,Rc,A,B,C三相总气隙磁通分别为Φa,Φb,Φc,总漏磁磁阻和漏磁磁通为Rmb和Φmb,总气隙磁通为Φδ。

图5 简化后的SPMB电机等效磁路图
得到A,B,C三相的磁导分别是:
(18)
(19)
(20)
式中:g0为SPMB电机的气隙厚度,αa,αb,αc分别为A,B,C三相定子齿和转子齿之间相互重叠的角度。
当三相极距相同时,三相磁导和为:
(21)
式中:Rδ=Ra//Rb//Rc,αδ=αa+αb+αc。由式(18)~式(21)可知,如果保持三相定转子重叠角αδ为一个常数可以减少永磁工作点随电机转动而发生的变化。
因此,取定子极弧系数Cs=0.5,即定子齿宽极弧βs=θcs/2。可得三相定转子重叠角:
(22)
(23)
(24)
无论转子处在任何位置。三相定转子重叠角之和不变,即:
(25)
3.3 永磁体尺寸
永磁材料直接决定了永磁电机的性能。由于永磁材料成本相对较高,永磁电机造价的高低和永磁体的用量有着直接的关系。
由图5可以计算电机的气隙磁通:
(26)
永磁体对外磁路提供的磁通:
(27)
式中:Bδpm为永磁体作用时的气隙磁密。
图6为钕铁硼的退磁特性曲线,退磁曲线接近一条直线。
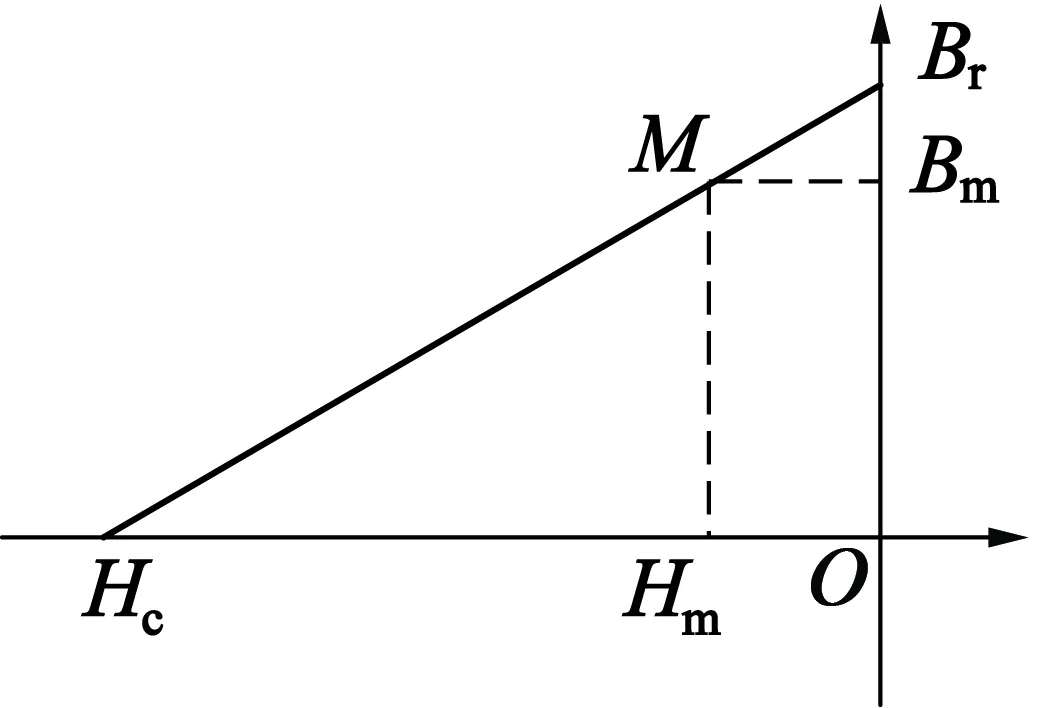
图6 永磁材料去磁特性曲线
如图6所示,当电机永磁工作点在M时,由图可得:
(28)
(29)
式中:Bm,Hm分别为永磁体工作点M处的磁密和磁场强度。
根据磁路定律,可得:
(30)
式中:hpm为永磁体厚度,Hδ为电机气隙中磁场强度,因此永磁磁化方向的厚度可由式(28)~式(30)求得:
(31)
4 有限元验证
根据理论分析计算,初步确定的SPMB电机主要尺寸参数如表1所示。
根据表1中的电机尺寸建立二维有限元模型如图7所示。由于该电机永磁体位于定子轭部,泄漏至定子外部的磁通不容忽略,所以需将电机仿真模型的求解区域进行扩展,并将半径为R0的空气圆外围设为零磁位面。

图7 双绕组SPMB电机二维有限元模型
电枢绕组空载,加载悬浮电流Is=2 A,YA,YB,YC相悬浮绕组按照理想顺序导通,不同转子位置下的悬浮力如图8所示。由图可以看出,Fx随转子位置角有着较大的变化,而Fy保持相对的稳定,且径向悬浮力的变化位置与悬浮电流换相位置吻合,因此可通过对6套悬浮绕组进行独立的控制来实现转子的稳定悬浮。
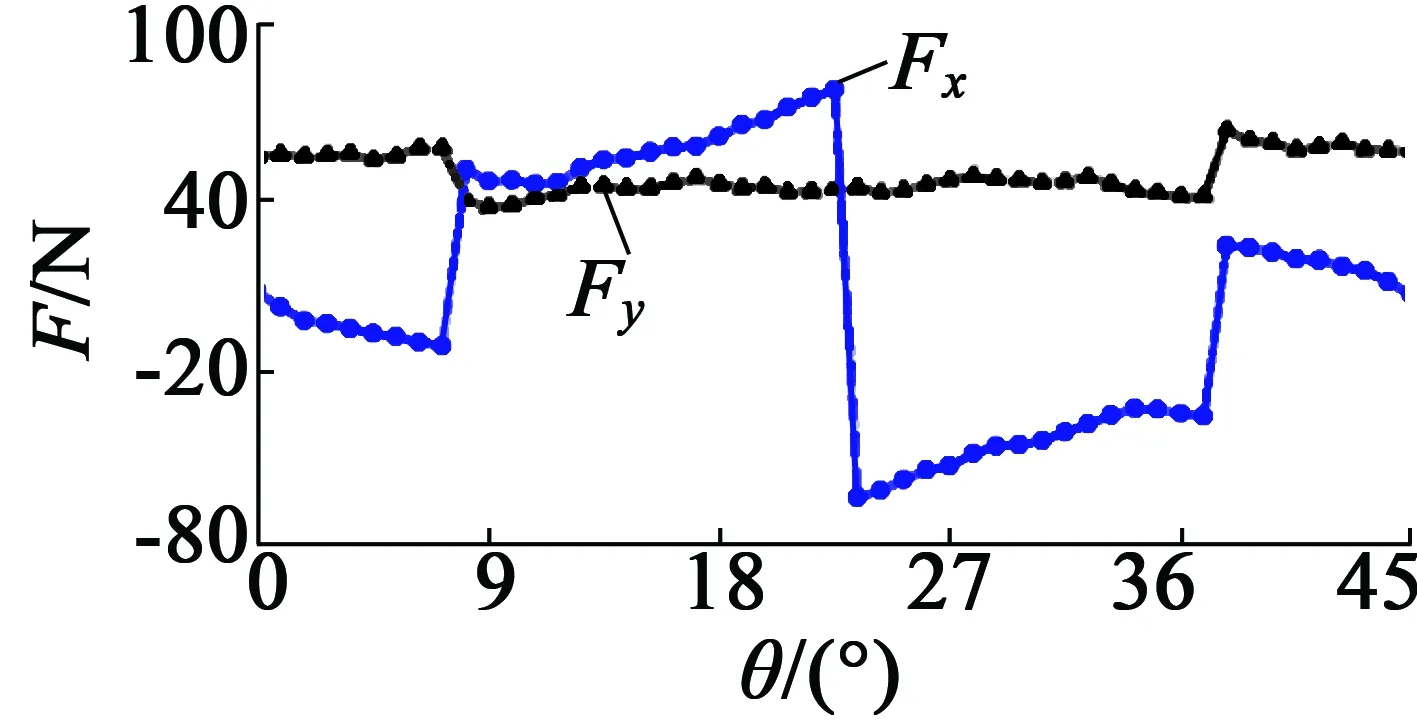
图8 悬浮力
图9为电枢绕组加载2.73 A电枢电流、Y相悬浮绕组加载-10~10 A悬浮电流情况下的电磁转矩。可以看出,悬浮电流对电磁转矩有一定的扰动,但是从平均电磁转矩与电枢电流的关系上看,悬浮电流对电磁转矩的影响可以忽略不计。

图9 电磁转矩
5 结 语
本文提出一种三相定子12/8极定子永磁型无轴承电机,阐述了其结构特点和径向悬浮力产生机理,推导建立了SPMB电机的功率尺寸方程,详细给出了确定电机主要尺寸参数的计算方法,并利用有限元仿真建模进行了验证,仿真结果可以看出该电机电磁转矩和径向悬浮力均有较好的输出特性。
[1] BOSCH R.Development of a bearingless electric motor[C]//In Proceeding of the International Conference on Electrical Machines.1988(3):373-375.
[2] CHIBA A,SANTISTEBAN J A.A PWM harmonics elimination method in simultaneous estimation of magnetic field and displacements in bearingless induction motors[J].IEEE Transaction on Industry Applications,2012,48 (1):124-131.
[3] 孙玉坤,袁野,黄永红,等.磁悬浮开关磁阻电机及其关键技术发展综述[J].电工技术学报,2015,30(22):1-8.
[4] 曹鑫,邓智泉,杨钢, 等.一种无轴承开关磁阻电机独立控制策略[J].中国电机工程学报,2008,28(24):94-100.
[5] 王喜莲,葛宝明,王旭东.一种无轴承开关磁阻电机悬浮性能分析[J].电机与控制学报,2013,17(1):7-12.
[6] 朱熀秋,张涛.无轴承永磁同步电机有限元分析[J].中国电机工程学报,2006,26(3):136-140.
[7] SUN X,CHEN L,YANG Z.Overview of bearingless permanent magnet synchronous motors[J].IEEE Transaction on Industrial Electronics,2013,60(12):5528-5538.
[8] 程明,张淦,花为.定子永磁型无刷电机系统及其关键技术综述[J].中国电机工程学报,2014(29):5204-5220.
[9] ZHAO W X,CHENG M,HUA W,et al.Back-EMF harmonic analysis and fault-tolerant control of flux-switching permanent-magnet machine with redundancy[J].IEEE Transactions on Industrial Electronics,2011,58(5):1926-1935.
[10] JIA Hongyun,FEI Shumin,CHENG Ming,et al.Design and electromagnetic performance analysis of a new stator-permanent magnet bearingless machine[C]//International Conference on Electrical Machines and System.IEEE,2015:1995-1998.
[11] JIA H Y,WANG J N,CHENG M,et al.Mathematical model of radial suspending force for a new stator-permanent magnet bearingless machine[J].IEEE Transactions on Magnetics,2015,51(11):1-4.
Design of Stator Permanent Magnet Bearingless Motor with Double-Winding
LIQuan,JIAHong-yun,XUFang,YUANAn-fu,CAOYong-juan
(Nanjing University of Information Science and Technology,Nanjing 210044,China)
A stator permanent magnet bearingless motor with double-winding (SPMB) machine was proposed. The topology structure and radial suspension force principle were introduced. The power equation was derived, which lays a foundation for the initial design of the machine. Stator and rotor pole arcs and permanent magnet size were calculated using the equivalent magnetic circuit method. Its characteristics, including radial suspension force and electromagnetic torque were analyzed by using the finite element method. The calculation results validate the design method and the theoretical analysis.
stator permanent magnet; bearingless; radial suspension force; power equation; magnetic circuit
2016-07-08
TM351
A
1004-7018(2017)01-0015-04
