基于神经网络分类算法的电机轴承故障检测方法
2017-03-09刘国庆史小春
刘国庆,史小春,廖 强
(1.四川工程职业技术学院,德阳 618000;2.电子科技大学,成都 611731)
基于神经网络分类算法的电机轴承故障检测方法
刘国庆1,史小春1,廖 强2
(1.四川工程职业技术学院,德阳 618000;2.电子科技大学,成都 611731)
针对电机轴承故障的检测问题,提出一种结合移除非故障分量(RemovingNon-bearingFaultComponent,RNFC)滤波器和多层感知器(Multi-LayerPerceptron,MLP)神经网络分类器的电机轴承故障检测方法。首先,利用神经网络设计一种RNFC滤波器,滤除与故障不相干的信号,只输出各种故障信号分量。然后,利用Levenberg-Marquardt算法训练MLP神经网络来构建故障分类器,并从RNFC滤波器输出的故障信号中提取4种时域特征(均方根、方差、偏度和峰度),作为故障分类器的输入。最后,实现对内圈缺陷、外圈缺陷和滚动体故障的检测。实验结果表明,该方法能够准确检测故障且对环境噪声具有鲁棒性。
电机轴承;故障检测;Levenberg-Marquardt算法;非故障分量滤波器;神经网络分类器;时域特征
0 引 言
异步电动机具有高可靠性和高性能等优点,然而也会出现一些故障[1]。轴承故障是大部分机械故障的主要来源[2]。轴承故障产生的振动影响具有相对较低的能量,且往往伴随着高能量噪声[3]。
目前,电机轴承故障检测技术主要分为3类:基于信号、基于知识和基于模型技术[4]。其中,基于信号的故障检测技术的基础是分析测量信号的频谱分量。常用的频域分析方法有快速傅立叶变换(FastFourierTransform,FFT)。然而,由于大功率噪声的存在,常规FFT方法很难从频谱中获得轴承故障信号。为此,形成了多种先进的频谱分析方法,例如短时傅立叶变换、小波变换(WaveletTransform,WT)和Park矢量法等[5]。为了克服噪声的影响,学者们开发了多种先进的轴承故障检测方法。例如,文献[6]对振动信号进行WT频域分析,提取频域特征作为神经网络(NeuralNetwork,NN)输入来检测轴承故障。然而,无用信号会降低神经网络的分类精度。为此,文献[7]在使用NN进行故障识别前,对振动信号进行维纳滤波,以去除噪声和无用信号,一定程度上提高了NN的分类精度。然而,该方法能够识别的故障种类很有限。
本文提出了一种结合移除非故障分量(RemovingNon-bearingFaultComponent,RNFC)滤波器和多层感知器(MultilayerPerceptron,MLP)神经网络分类器的电机轴承故障检测方法。利用RNFC滤波器滤除无关信号,接着提取4种时域信号特征,并利用Levenberg-Marquardt算法来训练MLP神经网络分类器,对故障进行分类识别。结果表明,提出的方法具有较高的检测率,且对环境噪声具有鲁棒性。
1 提出的故障检测方法
大部分轴承故障检测方法都是基于振动信号分析,包括健康状态时和故障时的信号[8]。但是,分析健康时的信号对故障检测和分类没有作用,且浪费计算资源。为了避免分析非轴承故障分量(即健康部分),提高故障检测效率。本文方法中,首先基于神经网络设计一种RNFC滤波器,滤除与故障不相干的信号,只输出各种故障信号分量。然后,利用MLP神经网络构建故障分类器,从RNFC滤波器输出的故障信号中提取特征,作为故障分类器的输入,进而实现对故障的检测。系统整体结构如图1所示。

图1 提出的故障检测方法结构图
1.1 非故障分量滤波器
移除非轴承故障分量(RNFC)滤波器框图如图2所示,变量名定义如下:
x(n):电机振动信号;y(n):估计的振动信号中与故障不相关的部分(非轴承故障分量);e(n):振动信号中的故障部分;n0:数据样本数。
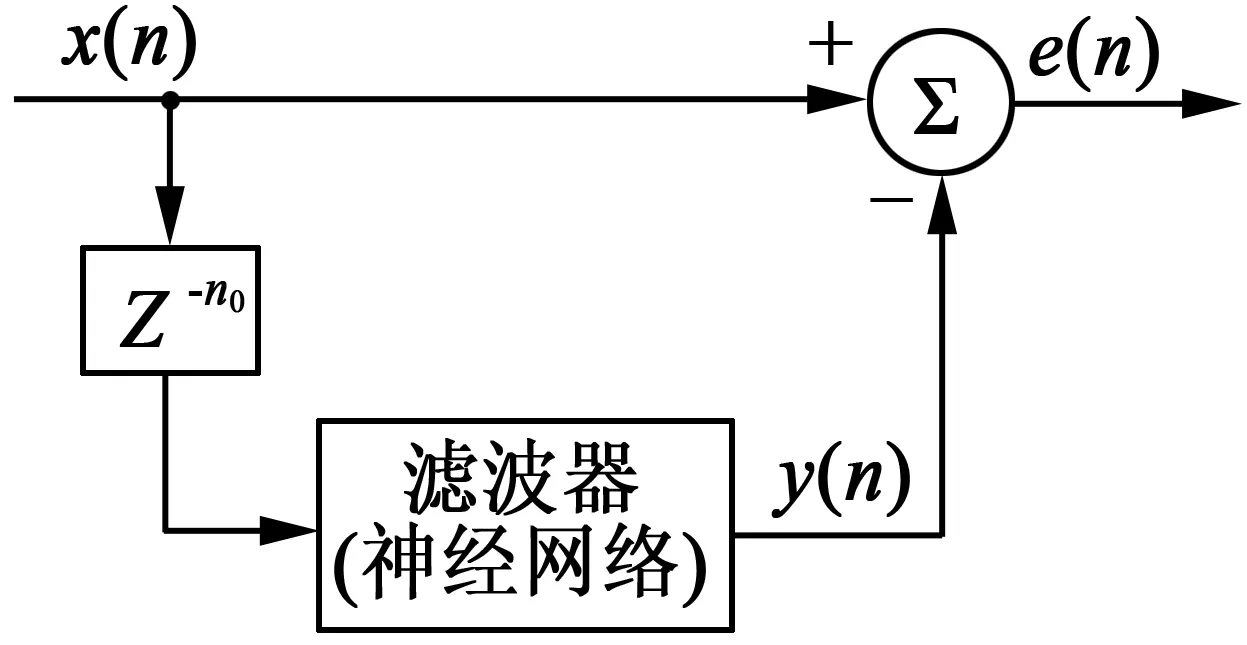
图2 移除非轴承故障分量(RNFC)滤波器
多种算法可用于设计RNFC滤波器,例如自适应横向滤波器、经典最小均方(LeastMeanSquare,LMS)算法、有限脉冲响应/无限脉冲响应、维纳滤波算法、递归最小二乘算法(RecursiveLeastSquare,RLS)和神经网络(NN)算法[9]。本文基于一种自适应线性神经网络构建RNFC滤波器,其具有purelin激励函数,结构如图3所示。运用监督训练方法获取目标(非故障部分),网络输入p和目标t如下:
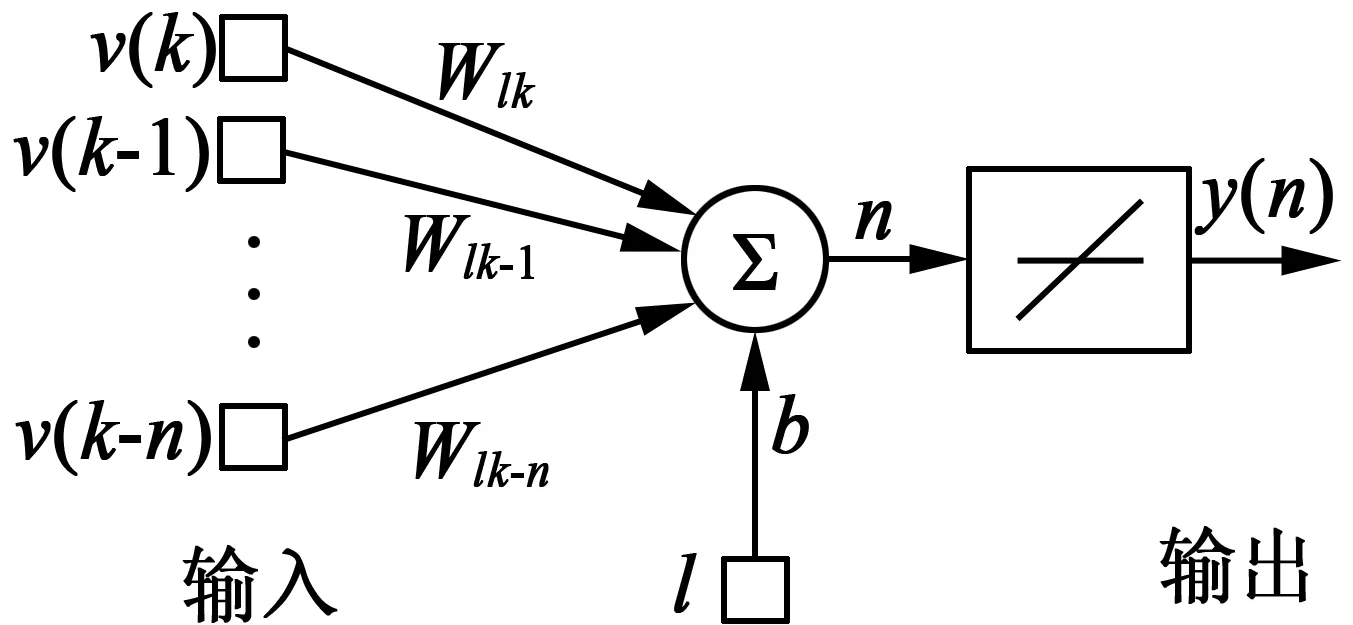
图3 自适应线性神经网络的结构
式中:shealthy(k)为健康异步电机的采样振动信号(k为样本数)。
为了实现更好的性能,将输入向量归一化到[0,1]范围内,将均方差作为神经网络的性能指标,并在训练过程中最小化该指标。这个过程中,由LMS算法获得神经网络参数(权重(w)和偏置(b)),并构建成参数向量X[10],神经网络的输入向量Z定义:
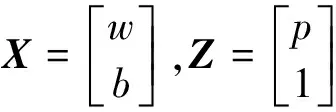
(1)
基于式(2),将方差总和作为成本函数:
(2)
式中:
E[t2]-2XTE[tZ]+XTE[ZZT]X
(3)
令
(4)
则有:
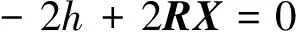
(5)
最后通过下式获得权重和偏置:
(6)
利用健康和各种故障条件下的信号数据集来训练RNFC滤波器中的自适应线性神经网络。训练完成后,当输入的振动信号包括健康和故障部分,该神经网络滤波器会识别健康部分,然后从输入振动信号中除去。RNFC滤波器的输出仅包括故障部分的信息,用于后续电机故障的检测和分类。但是,该信息的仅能检测故障,不能确定故障类型。为此,本文将构建第2个神经网络来识别故障。
1.2 基于MLP神经网络的故障分类
轴承状态分成4类[11]:(1) 健康状态;(2) 内圈缺陷故障;(3) 外圈缺陷故障;(4) 滚动体故障。文献[12]比较了用于轴承故障检测的径向基函数、MLP和概率神经网络,结果表明MLP在检测率方面较优且速度快。因此,本文采用MLP神经网络作分类器,其结构如图4所示。

图4 多层感知器网络的结构
需要从RNFC滤波器输出的故障信号中提取适当的特征,来训练基于MLP神经网络的分类器。本文选择4个时域特征,分别为:均方根、方差、偏度和峰值,来作为MLP神经网络故障分类器的输入特征,输入特征为:

(7)
均方根计算式:
(8)
式中:N为样本总数,μi为第i段的平均值,定义为:
(9)
方差计算式:
(10)
偏度计算式:
(11)
峰度计算式:
(12)
本文采用Levenberg-Marquardt算法来训练该网络,Levenberg-Marquardt算法是一种求解非线性最小二乘问题的有效方法,用来实现权值和阈值的调整。该算法的性能指标为方差总和:
(13)

根据参数向量X最小化性能指标:
(14)

(15)
(16)
式中:
(17)
雅可比矩阵J(X)定义:
(18)
另一方面,根据高斯-牛顿算法可省略式(16)右侧第二项,即R(X),因此,Hessian矩阵变为:
(19)
最终Levenberg-Marquardt参数的更新公式变为:
(20)
注意,μnI加入到JT(X)J(X),作为修正项,防止Hessian矩阵病变。μn为学习因子,μn越小,Levenberg-Marquardt算法与高斯-牛顿算法越相似。Levenberg算法的优势是高速收敛性[13]。
2 实验及分析
采用1.2kW,380V,1 500r/min,4极的三相异步电机[14]作为实验平台,轴端和风扇端轴承均为6205-2Z。振动信号由研华PCI-1711数据采集卡采集,使用B&K4395加速度计,采样频率为32kHz。实验装置如图5所示。由于提出的方法不依赖于特征缺陷频率,所以能够在不同负载条件下使用。
采样640个周期的振动信号样本,用来训练RNFC滤波器。RNFC滤波器设计中,设定一个单位的采样数据延迟(n0=1),因此输入原型定义:
目标为:
训练完成后,RNFC滤波器从采样的振动信号中提取出故障数据,以ptest形式表示。
将不同时期的故障振动信号作为RNFC滤波器的输入,然后从RNFC滤波器的输出中随机选择157个周期故障信号,来训练MLP神经网络分类器。

图5 轴承故障检测实验装置
四类不同故障状态下的RNFC滤波器输出波形如图6所示。可以看出,正常情况下,输出信号幅值几乎为0,这也验证了RNFC滤波器的性能。
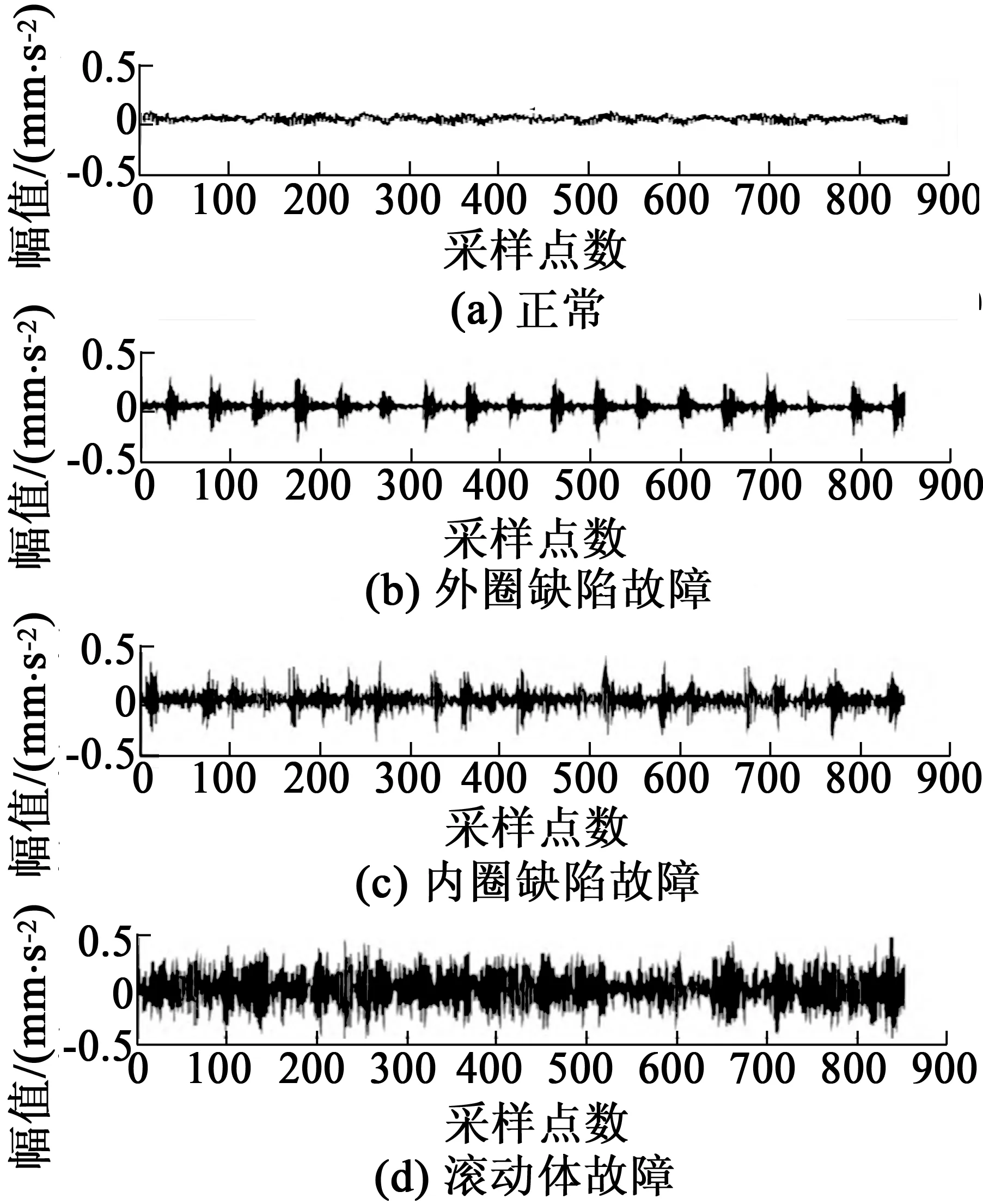
图6 四类故障的RNFC滤波器输出
将滤波器输出的20个周期的信号作为一组,并计算4种时域特征。将特征输入到MLP故障分类器,分类器的四个输出向量定义为[0 0]T,[0 1]T,[1 0]T,[1 1]T,分别对应于健康、外圈缺陷、内圈缺陷和滚动体故障。所以,对于MLP神经网络分类器,其输入层神经元数量为4,输出层神经元数量为2。表1描述了测试数据中提取的各种时域特征。

表1 测试数据中提取的各种时域特征
本文MLP分类器采用具有“tansig”传递函数的隐层和“satins”激励函数的输出层,用来检测轴承故障类型。可以通过适当增加隐层神经元数量和隐层数量来提高模式识别性能,但隐藏层数过高也会导致网络过度训练。
对于MLP神经网络,构建4种具有不同隐层神经元数和隐层数的结构,其中隐层的数量分别为1,1,2和3。表2给出了具备RNFC滤波器和MLP神经网络分类器的故障检测结果。表3给出了无RNFC滤波器时的故障检测结果。

表2 具有RNFC滤波器的故障检测
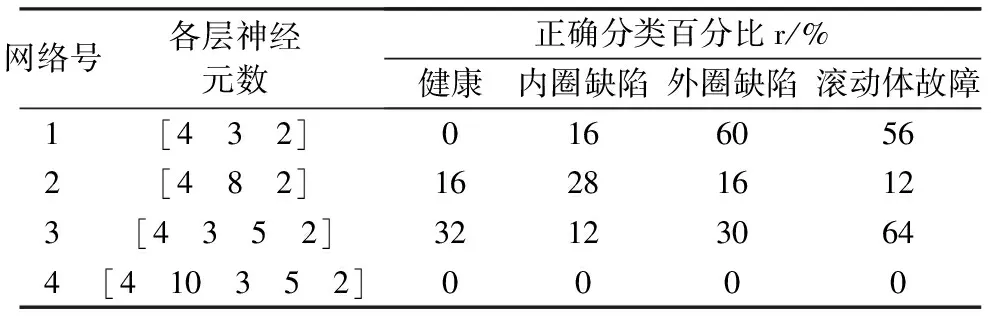
表3 直接故障检测(无RNFC滤波器)
通过比较表2和表3中的故障检测结果可以看出,无RNFC滤波器的检测系统的检测率明显较低,从而验证了提出方法的有效性。另外,还可以看出,当网络结构为[4 10 3 5 2],即隐层数量为3时,分类器几乎无法工作。这是因为该分类器的输入和输出类别都较少,过多的隐层数导致过度训练,从而使其无法工作。
表4给出了存在低质量采样信号时,即存在环境噪声,有和没有RNFC滤波器时的故障检测结果。注意,表4中只列出了前3种网络结构,这是因为从上述实验得知,当网络中隐含层数为3时,分类器无法工作。

表4 采样信号中存在噪声时的故障检测
从表4中可以看出,当采样信号中存在噪声信号时,具有RNFC滤波器的故障检测系统能够明显提高检测性能。这是因为,RNFC滤波器中的自适应线性神经网络能够分类出故障和非故障信号,非故障信号包含了正常和噪声信号,并进行移除。使后续的特征提取和故障分类过程不受噪声影响,提高了对采样信号质量的鲁棒性,因此可以用于嘈杂工业环境中进行高性能故障检测。
3 结 语
本文提出了一种用于电机轴承故障检测和分类的方法,首先利用神经网络设计一种移除非轴承故
3 结 语
障分量(RNFC)滤波器,从采样信号中滤去非轴承故障分量。然后,利用多层感知(MLP)神经网络构建故障分类器,从RNFC滤波器输出的信号中提取时域特征,作为MLP神经网络的输入,从而检测轴承故障。构建实验平台进行实验,在不同MLP神经网络结构下,比较了使用和不使用RNFC滤波器时的检测结果。结果表明,本文提出的结合RNFC滤波器和MLP分类器的方法具有优良的检测性能,且对环境噪声具有鲁棒性。
未来工作中,将考虑将本文方法应用到其它电机故障检测中,例如转子断条或定子故障等。
[1] 刘长良,武英杰,甄成刚.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J].中国电机工程学报,2015,35(13):3358-3365.
[2] 李珂,邰能灵,张沈习.基于小波包熵和概率神经网络的微特电机轴承故障监控[J].微特电机,2016,44(4):37-39.
[3]TIANJ,MORILLOC,AZARIANMH,etal.Motorbearingfaultdetectionusingspectralkurtosis-basedfeatureextractioncoupledwithk-nearestneighbordistanceanalysis[J].IEEETransactionsonIndustrialElectronics,2016,63(3):1793-1803.
[4] 张登峰,张志飞,章兢.基于非线性映射的分类器及其在变压器故障诊断中的应用研究[J].湘潭大学自然科学学报,2015,37(3):82-92.
[5]JENAD,SINGHM,KUMARR.Radialballbearinginnerracedefectwidthmeasurementusinganalyticalwavelettransformofacousticandvibrationsignal[J].MeasurementScienceReview,2012,12(4):141-148.
[6]ZAREIJ.Inductionmotorsbearingfaultdetectionusingpatternrecognitiontechniques[J].ExpertsystemswithApplications,2012,39(1):68-73.
[7]ABBASIR,GHAZALM,KAZEMIMG.Statorwindingfaultdetectionininductionmotorsusingwienerfilter[J].InternationalReviewofElectricalEngineering,2012,7(4):4800-4807.
[8] 谢国民,佟莹,陆文斌.小波在采煤机异步电动机故障诊断中的应用[J].控制工程,2013,20(4):711-714.
[9]CHENGS,HABETLERTG,MAYORJR,etal.Generalizedbearingroughnessfaultdetectioninclaw-polegenerators[C]//2013IEEEEnergyConversionCongressandExposition.IEEE,2013:4432-4437.
[10]ZHONGF,LIH,WUQ,etal.AfaultdetectionalgorithmforturbopumpbasedonliftingwaveletandLMS[C]//2013IEEEInternationalConferenceonMechatronicsandAutomation(ICMA).IEEE,2013:348-353.
[11] 赵志宏,杨绍普.基于小波包变换与样本熵的滚动轴承故障诊断[J].振动、测试与诊断,2012,32(4):640-644.
[12]SAMANTAB,AL-BALUSHIKR,AL-ARAIMISA.Artificialneuralnetworksandgeneticalgorithmforbearingfaultdetection[J].SoftComputing,2012,10(3):264-271.
[13]ZHANGX,XIAOL,KANGJ.ApplicationofanimprovedLevenberg-Marquardtbackpropagationneuralnetworktogearfaultlevelidentification[J].JournalofVibroengineering,2014,16(2):855-868.
[14] 张帅,袁敏,孔令波,等.高效三相异步电动机性能测试与数据分析[J].微特电机,2015,43(3):22-26.
MotorBearingFaultDetectionMethodBasedonNeuralNetworkClassificationAlgorithm
LIU Guo-qing1,SHI Xiao-chun1,LIAO Qiang2
(1.SichuanEngineeringTechnicalCollege,Deyang618000,China;2.UniversityofElectronicScienceandTechnologyofChina,Chengdu611731,China)
Fortheissuesthatthemotorbearingfaultdetection,amotorbearingfaultdetectionmethodbasedonremovingnon-bearingfaultcomponent(RNFC)filterandmultilayerperceptron(MLP)neuralnetworkclassifierwasproposed.First,itbuiltaRNFCfilterbasedonneuralnetworktoremovethesignalwhichhasnothingtodowiththefault,onlyoutputofvariousfaultsignalcomponents.Then,itconstructedafaultclassifierbasedonMLPneuralnetworkwhichtrainedbyLevenberg-Marquardtalgorithm.Thefourfeatures(RMS,variance,skewnessandkurtosis)wereextractedfromthefaultsignaloutputofRNFCfilter,astheinputoffaultclassifier.Finally,thedetectionoftheinnerring,theouterringandtherollingelementfaultwasrealized.Theexperimentalresultsshowthatproposedmethodcanaccuratelydetectfaultandrobusttonoise.
motorbearing;faultdiagnosis;Levenberg-Marquardtalgorithm;removingnon-bearingfaultcomponentfilter;neuralnetworkclassifier;timedomainfeatures
周璞,硕士,高级工程师,研究方向为船舶辅机。
2016-07-15
四川省科技厅计划项目(2015JY0178)
TM
A
1004-7018(2017)01-0030-04
