基于动网格降阶算法的机翼颤振边界预测

仲继泽， 徐自力

(西安交通大学 机械结构强度与振动国家重点实验室，西安 710049)

基于动网格降阶算法的机翼颤振边界预测

仲继泽， 徐自力

(西安交通大学 机械结构强度与振动国家重点实验室，西安 710049)

基于弹性体动网格技术，发展了一种用于机翼流场网格变形的降阶算法。将流场网格所包围的空间区域视为虚拟弹性体。以虚拟弹性体变形的静力平衡方程为基础，结合机翼的振动控制方程，推导了机翼与虚拟弹性体的整体的振动控制方程。通过模态叠加方法计算机翼和流场网格节点的位移，进而得到变形后的流场网格。考虑到机翼颤振多为1阶弯曲和扭转振动，所以在流场网格节点位移的计算中只需考虑1阶弯曲和扭转振型。为了保证计算精度，在计算中同时考虑了2阶弯曲和扭转振型。RANS方程为流体控制方程，采用Spalart-Allamras湍流模型，结合动网格降阶算法，对AGARD Wing 445.6颤振边界进行了流固耦合计算。计算结果相对于实验值的偏差小于2%，且与已有的弹性体动网格方法比，计算时间减少了54.8%。

机翼颤振；流固耦合；动网格；虚拟弹性体；模态叠加

机翼颤振是一种典型的流固耦合问题，它会使机翼产生损坏。美国空军F-117战机机翼因颤振发生破坏，导致该战机坠毁[1]。美国洛克希德-马丁公司的验证机在飞行实验中，机翼因发生颤振而折断[2]。因此，机翼与空气之间的流固耦合问题一直是航空工程领域研究的热点。

传统的机翼颤振预测的数值方法主要有V-g和p-k方法[3]。在传统方法中，假设机翼做简谐振动，并采用线性气动模型分析机翼周围流场。对于亚音速流动，采用偶极子格网法[4]分析机翼周围的流动。对于超音速流动，采用piston理论[5]分析机翼周围的流动。这些传统方法的计算效率高，而且对亚音速及超音速颤振的预测精度较高。但是采用传统方法预测机翼跨音速颤振时，需要通过缩比模型的风洞试验对所预测的颤振流速进行修正。而缩比模型的设计及其实验数据的分析，通常需要1年时间[6]。这会严重拖慢飞行器的研发进度。鉴于上述原因，航空工程领域的研究人员引入了基于CFD(Computational Fluid Dynamics)/CSD(Computational Structural Dynamics)的流固耦合方法，以预测机翼颤振边界[7-8]。流固耦合方法可以分为弱耦合和强耦合两种算法[9]。弱耦合算法中，流场分析在时间域上先于振动分析一个时间步，容易累积误差，引起发散。强耦合算法中，流场与机翼振动通过每一迭代步的气动力及位移传递实现时间同步求解，具有更好的鲁棒性。

机翼振动会改变流场的边界，在流固耦合计算中为了考虑边界变动对流场的影响，必须对流场网格节点坐标进行更新。目前所发展的网格变形方法主要有弹簧法[10]、弹性体方法[11]、温度体方法[12]及径向基函数方法[13]。与其他动网格方法相比，弹性体方法是一种基于物理模型的网格变形方法，把流场网格变形作为一个弹性体变形问题进行求解，更能贴近结构弹性变形的物理实际。另外，弹性体方法可以通过设置不均匀和各向异性弹性刚度等具体措施，保证变形过程中流场边界层网格的质量。因此，与其他的动网格方法相比，弹性体方法具有较强的网格变形能力，且变形后网格质量较高[14]。但是弹性体方法比较复杂，计算量大。尤其是以强耦合的方式对机翼颤振进行计算时，每一时间步都需要对流场网格变形进行多次迭代求解。所以在流固强耦合计算中，采用弹性体方法更新流场网格会耗费大量计算资源。鉴于此，本文在现有弹性体动网格技术[15-17]的基础上，发展了一种能够快速计算机翼流场网格节点位移的动网格降阶算法。采用频率及振型描述机翼及流场网格变形。通过求解模态坐标下解耦的动力学方程得到模态位移，然后采用模态叠加方法计算机翼流场网格节点的位移。考虑Wing 445.6的前4阶模态，采用流固强耦合方法计算了其无因次颤振流速，计算结果与实验值吻合很好。

1 控制方程

机翼附近的气流一般为黏性可压缩流动，可以采用RANS(Reynolds Averaged Navier Stokes)方程作为控制方程。

(1)

式中：Ω为有限控制体；∂Ω为有限控制体的表面；n为控制体表面外法向；W为守恒性流体向量；Fc为无黏通量；Fv为黏性通量。

(2)

式中：ρ为流体密度；u为流速；ur为流体相对流场网格的流速；E为流体总能；p为流体压力；τ为流体剪切应力张量；q为热流向量。

ur=u-ug

(3)

式中,ug为流场网格速度。

RANS方程不是封闭的，需要结合湍流模型来封闭方程。本文采用Spalart-Allamras模型[18]作为湍流模型。

机翼表面的气流压力，使机翼受到气动力的作用。在气动力作用下，机翼会产生振动。机翼振动的有限元控制方程为

(4)

式中：Mw为机翼总体质量矩阵；Cw为机翼总体阻尼矩阵；Kw为机翼总体刚度矩阵；Xw为机翼结构网格节点位移向量；Ffsi为机翼流固耦合面受到的气动力。

在流固耦合面处，即机翼表面，机翼振动会改变流场边界。因此，需要变更流场网格节点的位置。HUO等将流场网格所包围的空间区域视为虚拟弹性体，通过求解虚拟弹性体变形的静力平衡方程计算流场网格节点的位移。虚拟弹性体变形的静力平衡方程为

KeXe=0

(5)

式中：Ke为流场网格域虚拟弹性体的总体刚度矩阵；Xe为流场网格节点位移向量。

2 流场动网格的降阶算法

为了实现流场网格计算的降阶，本文将流场网格域视为虚拟弹性体，并将机翼和虚拟弹性体作为一个整体系统。本小节将推导机翼与虚拟弹性体的整体振动控制方程，给出动网格降阶算法的理论基础。

机翼网格节点可以分为流固耦合面节点和非流固耦合面节点两个部分，据此将机翼振动控制方程式(4)写成分块矩阵的形式。

(6)

式中：Xw_fsi为机翼网格流固耦合面节点位移向量；Xw_n_fsi为机翼网格非流固耦合节点位移向量。

流场网格节点也可以分为流固耦合面节点和非流固耦合面节点两个部分，据此将流场网格域虚拟弹性体变形的静力平衡方程式(5)写成分块矩阵的形式。

(7)

式中：Xe_fsi为流场网格流固耦合面节点位移向量；Xe_n_fsi为流场网格非流固耦合节点位移向量。

虚拟弹性体随机翼振动发生变形，即在流固耦合面处，虚拟弹性体与机翼的位移具有连续性。可以采用有限单元位移插值算法[19]，对机翼结构网格流固耦合面的节点位移Xw_fsi进行插值得到机翼流场流固耦合面节点的位移Xe_fsi。

Xe_fsi=NXw_fsi

(8)

式中,N插值系数矩阵。

因此，虚拟弹性体变形的静力平衡方程可以改写为

(9)

机翼和虚拟弹性体的整体的振动控制方程可以通过叠加机翼振动控制方程式(6)和虚拟弹性体变形的静力平衡方程式(9)得到。

(10)

采用模态分析得到机翼与虚拟弹性体同步振动系统的模态频率ω及质量归一化的正则振型Ψ，并通过坐标变换得到正则坐标下的解耦的动力学方程。

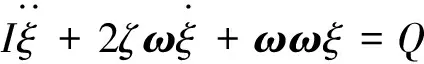
(11)

式中：I为单位矩阵；ξ为模态位移；ζ为模态阻尼比；Q为模态气动力。

(12)

(13)

(14)

动力学方程式(11)的分量形式为

(15)

可以通过Wilson-θ方法求解上述的模态方程计算出模态位移ξi，然后采用模态叠加方法计算机翼及流场网格节点的位移。

(16)

式中,n为参与机翼流固耦合振动的模态数。

本文将机翼和虚拟弹性体作为一个整体系统，通过模态分析得到机翼和虚拟弹性体的整体的模态，然后采用模态叠加方法计算机翼和流场网格节点位移。考虑到机翼颤振多为一阶弯曲或弯扭耦合振动[20]，所以在流场网格节点位移的计算中只需考虑一阶弯曲或扭转等低阶模态，从而达到降阶的目的。

3 流固耦合算法

本文采用强耦合算法对机翼颤振进行流固耦合分析。为加快收敛，采用稳态流场的计算结果作为瞬态流场的初值。流固耦合分析的流程为

(1)采用SIMPLE算法[21]求解RANS方程，计算出流场的流速，压力等变量。

(2)根据机翼流固耦合面上的流场压力分布计算机翼的气动力Ffsi，然后采用式(14)计算机翼的模态气动力Qi。

(3)通过求解模态动力学方程式(15)计算模态位移ξi，然后采用模态叠加法计算机翼流场网格节点位移。

(4)根据流场网格节点位移更新流场网格节点坐标，在新网格的基础上再次求解RANS方程，计算流场流速，压力等变量。

(5)观察计算的收敛情况，如果计算不收敛，则重复(2)～(4)，直到计算收敛，如果计算收敛，则进行下一时间步的计算。

流场压力、速度和总能的残差小于某一特定值时，我们认为计算收敛。这一特定值的选取是与具体问题相关的。在本文的AGARD Wing 445.6算例中，当压力残差<5.2×10-5，速度残差<2.4×10-5，总能残差<2.7×10-7时，我们认为计算达到收敛。

4 机翼和流场网格及网格变形

AGARD Wing 445.6[22]是由美国国家航天局兰利研究中心(NASA Langley Research Center)设计的颤振实验模型，具有完整的风洞实验数据，是目前国际上用于机翼流固耦合算法验证的标准算例。AGARD Wing 445.6采用NACA 65A004对称翼型，展长0.762 m，根弦长0.558 7 m，1/4弦线后掠角为45°，展弦比1.65，根梢比0.66，见图1。该机翼为木质材料，其展向弹性模量为3.15 GPa，展向垂直方向的弹性模量为0.416 2 GPa，剪切模量为0.439 2 GPa，泊松比为0.31，密度为393.5 kg/m3。考虑机翼的材料阻尼，选取的材料阻尼比为0.03。机翼网格见图2，共有8节点六面体单元5 974个，节点7 500个。

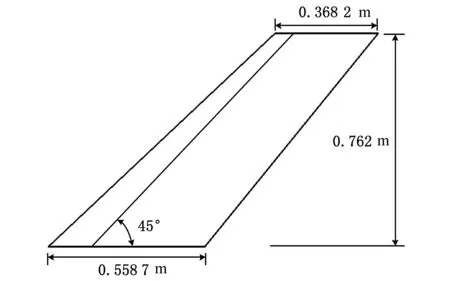
图1 AGARD Wing 445.6 几何尺寸Fig.1 Geometric configuration of AGARD Wing 445.6

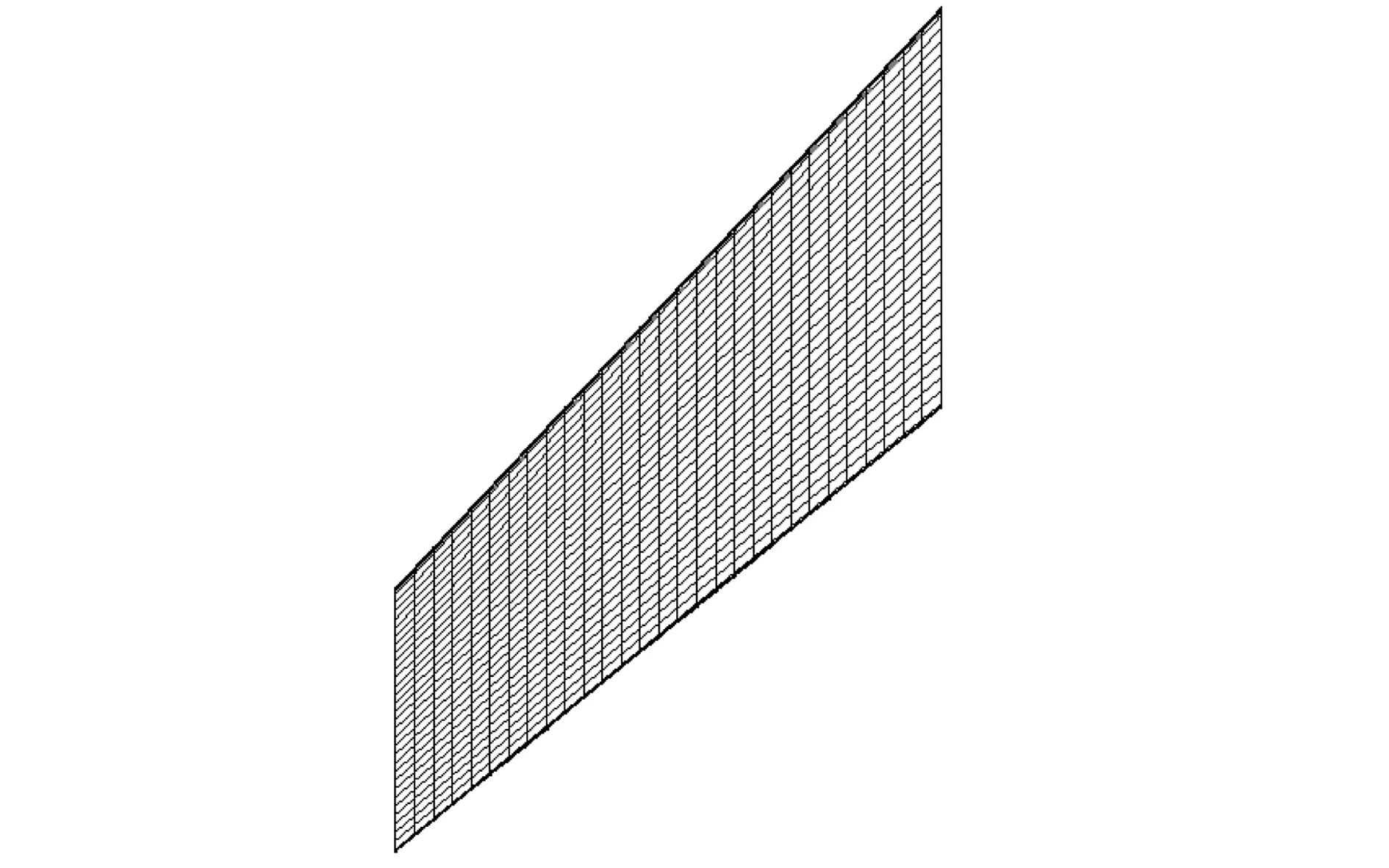
图2 AGARD Wing 445.6网格Fig.2 Mesh for AGARD Wing 445.6

边界层网格的大小直接影响流场的在机翼表面的微观流动特性，因此选取合适的边界层网格至关重要。本文根据机翼的特征长度(弦长)、流场的雷诺数和机翼壁面的Y+值，采用NASA所提供的经验公式确定边界层第一层网格的厚度。特征长度取翼尖弦长(0.368 2 m)。最大马赫数(1.141 Ma)时的流场雷诺数为6.5×105。为本文采用Spalart-Allmaras湍流模型，该模型要求Y+<2，本文取Y+=1。据此本文计算得到边界层第一层网格的厚度为1.0×10-5m。设定边界层每一层的网格厚度以1.2的比例逐层增加。

图3给出了采用不同数量的流场网格时计算得到的翼尖截面处上侧的压力分布。可以看出，随着流场网格的增多，计算结果逐渐趋于一致。流场网格数量为563 472时的计算结果与网格数量为649 872时的计算结果的相对偏差为0.02%。我们认为，当流场网格数量为563 472时，增加网格数量基本不会提升计算精度，反而会增加计算规模。因此，本文选取网格数量为563 472的流场网格为本文的计算网格。机翼流场网格见图4，共有节点588 080个。

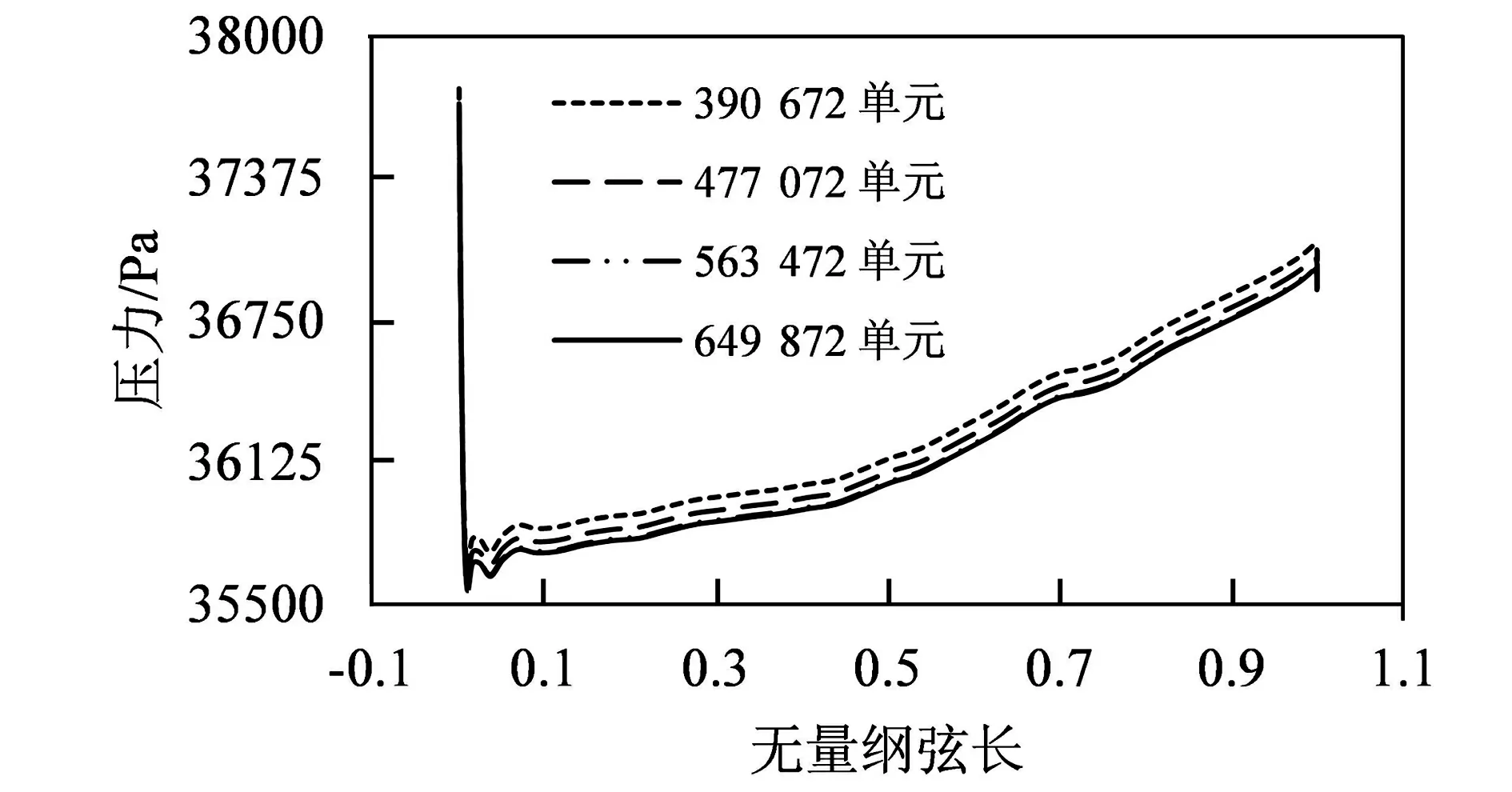
图3 Wing 445.6翼尖截面处上侧压力分布Fig.3 Pressure on the upside of the tip section of Wing 445.6

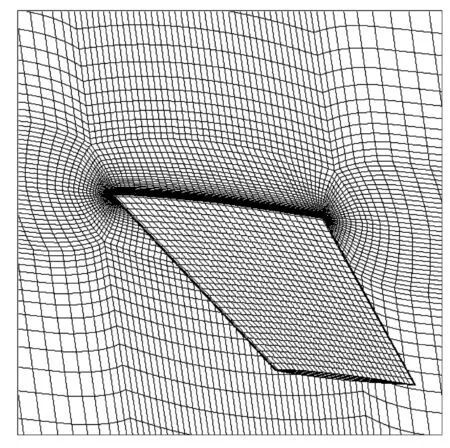
图4 AGARD Wing 445.6 流场网格Fig.4 Flow mesh for AGARD Wing 445.6

当设定虚拟弹性的为单一弹性模量时，流场网格变形过程中容易引发网格畸变(见图5(a))。为了避免流场边界层网格在变形过程中发生畸变，保证变形过程中流场网格的质量，本文设定流场网格域虚拟弹性体的弹性模量与流场网格的大小相关，见式(17)。

(17)

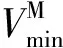
在流固耦合面处，流场边界层网格体积较小，其内部的虚拟弹性体的弹性模量较大。离边界层越远网格体积就越大，网格内部的弹性体弹性模量就越小。虚拟弹性体的弹性模量随网格体积的增加以指数规律减小。当流场网格随机翼振动发生变形时，边界层网格基本不发生弹性变形，而是随着机翼振动作整体的刚体运动，从而避免流场网格变形过程中边界层网格的畸变问题(见图5(b))。

图5 畸变和非畸变流场网格变形Fig.5 Flow mesh deformation with and without distortion

流场网格内部的虚拟弹性体的弹性模量的最大值为50 Pa，远小于机翼的弹性模量0.416 2 GPa。因此，与机翼的整体刚度矩阵相比，虚拟弹性体的总体刚度矩阵是小量。可以认为，虽然机翼在流固耦合面处与流场网格域的虚拟弹性体关联，但是虚拟弹性体不会改变机翼的固有振动频率及振型。采用本文的模态方法计算出的机翼的固有频率(见表1)，本文的计算结果与实验值吻合较好。机翼前4阶模态振型对应的流场网格变形(见图6)，可以看出流场网格变形整体比较平顺，没有出现网格畸变。

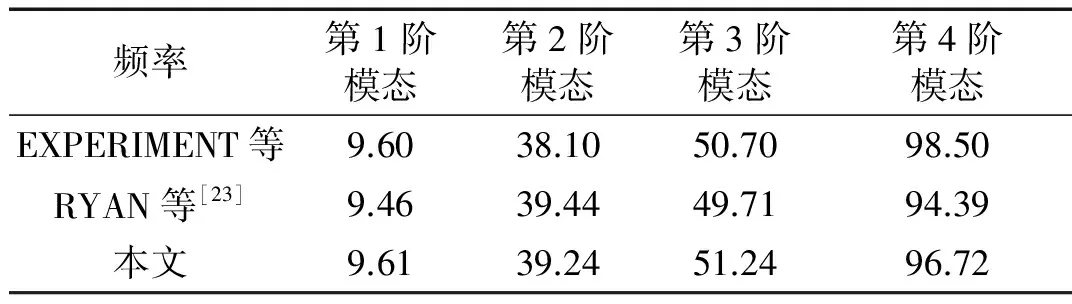
表1 AGARD Wing 445.6频率

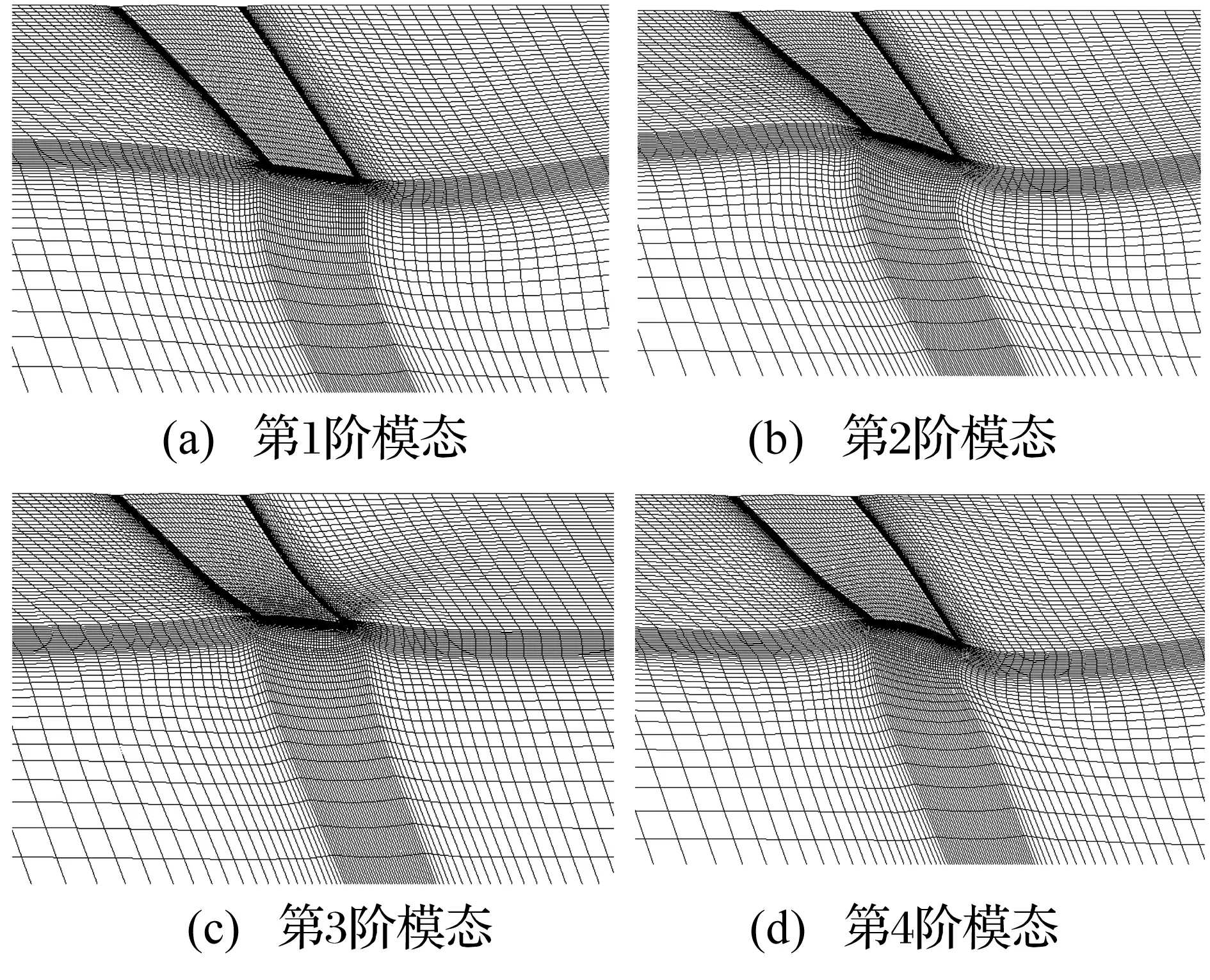
图6 AGARD Wing 445.6 不同模态下流场网格变形Fig.6 Flow mesh deformation against vibration mode for AGARD Wing 445.6

5 机翼颤振边界预测

通常采用无因次流速表征机翼颤振边界，表达式为

(18)

式中：vf为来流流速；b为翼根半弦长；ωα为机翼一阶扭转振动角频率；μ为质量比。

(19)

式中：m为机翼质量；ρ为空气密度；v(=0.13 m3)为参考体积。

在初始时刻，设置机翼第1～4阶的模态初始位移为0，初始速度为0.023，0.033，0.074和0.054。在来流马赫数为0.499的条件下，当无因次流速为0.424时，机翼各阶模态位移时间曲线(见图7)。各阶模态响应的模态位移幅值随着时间的推进逐渐减小，呈收敛趋势。即，机翼不会发生颤振。当无因次流速为0.468时，机翼各阶模态位移时间曲线(见图8)。各阶模态响应的模态位移幅值随着时间的推进逐渐增加，呈发散趋势。即机翼发生颤振。

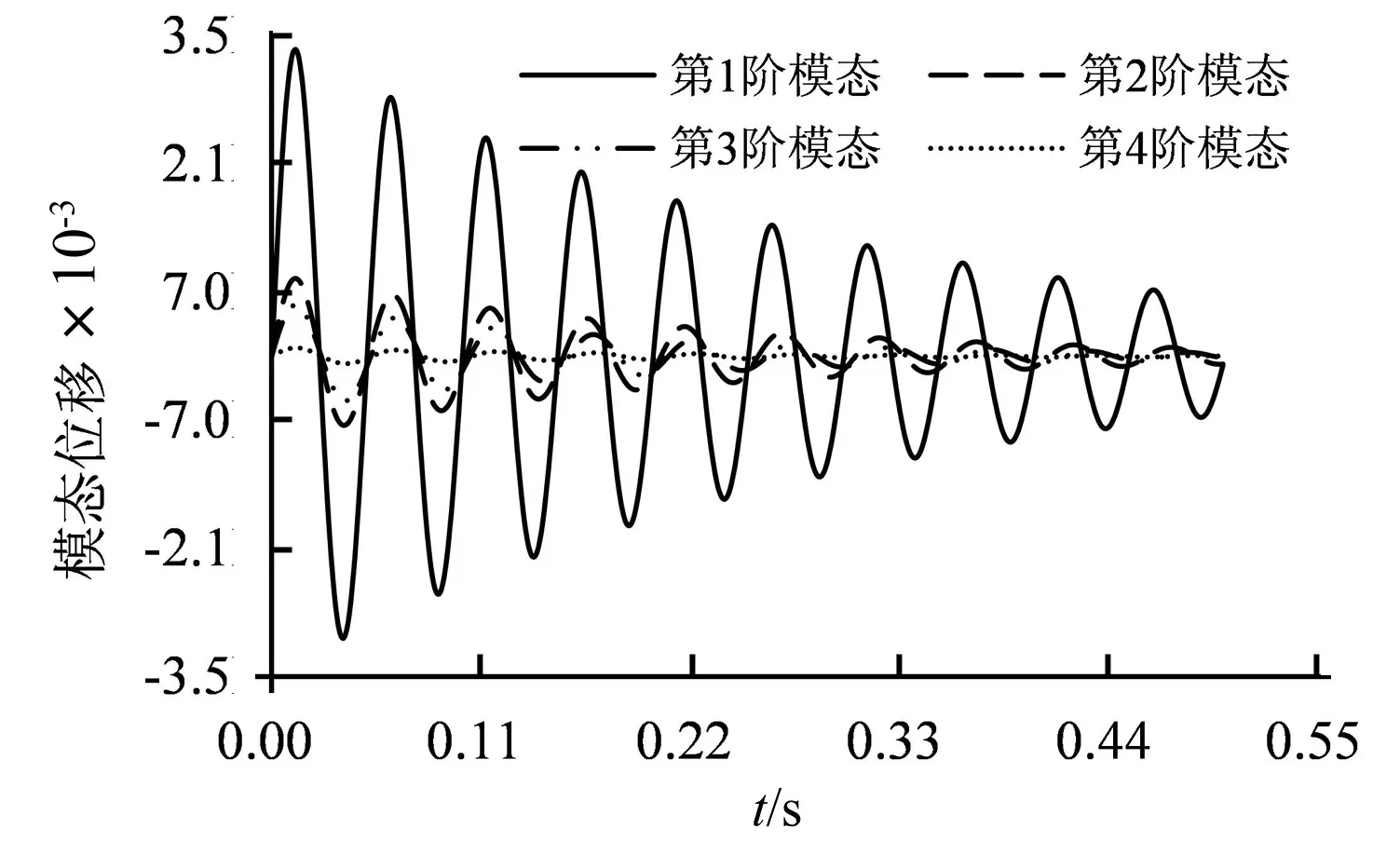
图7 无因次流速为0.424时的模态位移时间曲线Fig.7 Modal displacement vs time at reduced velocity 0.424

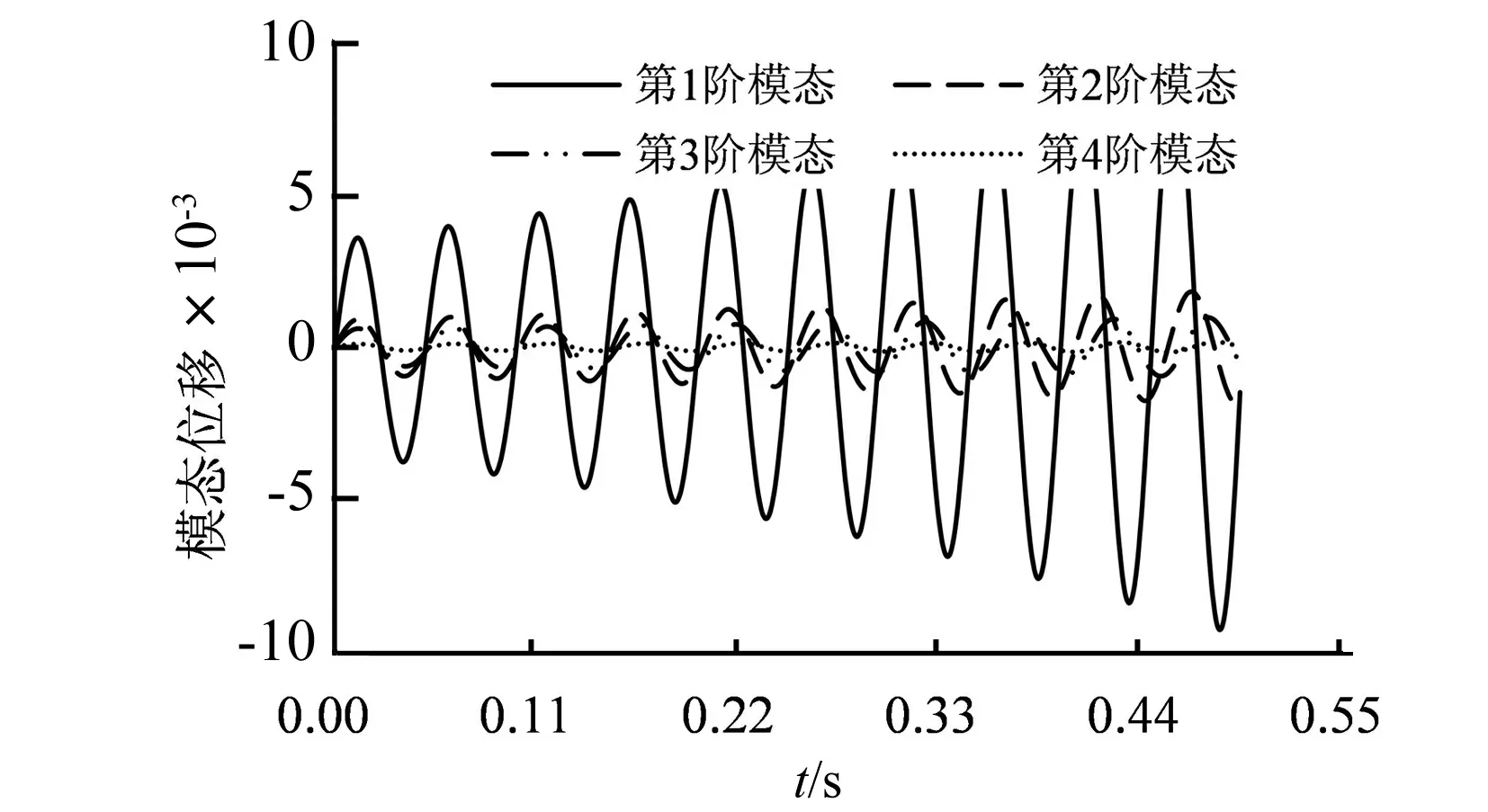
图8 无因次流速为0.468时的模态位移时间曲线Fig.8 Modal displacement vs time at reduced velocity 0.468

机翼振动的稳定性，可以采用对数衰减率(Logarithmic Decrement Ratio, LDR)进行评估。

(20)

式中：ln为自然对数符号；Ai+1为第个i+1周期的振动幅值；Ai为第i个周期的振动幅值。

在马赫数为0.499的条件下，机翼振动的对数衰减率与无因次流速的关系曲线(见图9)。在虚线的上方，LDR>0表示振动幅值随时间增大，机翼发生颤振。在虚线的下方，LDR<0表示振动幅值随时间减小，机翼不会发生颤振。曲线与虚线的交点处，LDR=0，表示振动幅值不随时间变化，可以认为机翼处于颤振临界点。在该颤振临界点处，无因次流速为0.452，机翼各阶模态位移时间曲线见图10。本文设置的时间步长为4×10-4s，采用4核心2.9 GHz CPU 计算出图10所示响应的一个周期，耗时14.1 h。而采用HUO等所提出的弹性体方法，耗时为31.2 h。本文的方法可以减少计算时间54.8%。

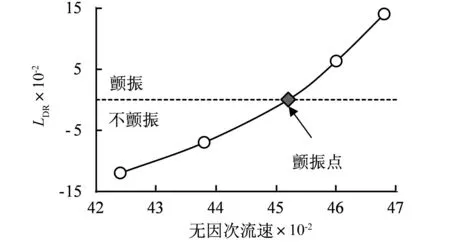
图9 马赫数为0.499时对数衰减率-无因次流速曲线Fig.9 LDR vs. reduced velocity at the Mach number 0.499

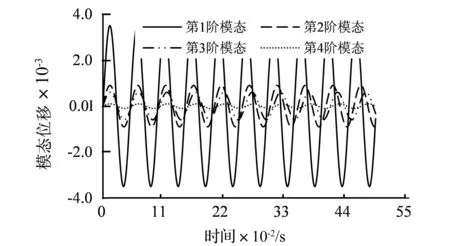
图10 无因次流速为0.452时的模态位移时间曲线Fig.10 Modal displacement vs. time at reduced velocity 0.452

本文计算出的Wing 445.6颤振边界，见图11。可以看出，同时考虑第1阶和第2阶的弯曲及扭转模态的计算结果优于只考虑第1阶模态的计算结果。将考虑第1和第2阶的计算结果与文献的结果对比如下：在亚音速区域(Ma=0.499,0.678)，本文的结果与CHEN等研究的结果基本一致，且均与实验值吻合较好。在跨音速区域(Ma=0.901，0.960)，本文的结果比CHEN等研究的结果更接近实验值。本文采用Spalart-Allamras湍流模型，CHEN等采用Baldwin-Lomax湍流模型。由此可见，Spalart-Allamras模型比Baldwin-Lomax模型更好的模拟机翼的跨音速流动。这与文献[24]的结论是一致的。本文和CHEN等采用RANS方程作为流体的控制方程，计算出的机翼的超音速(Ma=1.141)颤振边界，与实验值均有较大偏离。IM等[25]对这一现象进行了研究，发现RANS方程不能准确捕捉超音速流动中激波边界层干扰及其所引发的流动分离现象，导致计算出的超音速颤振边界偏差较大。整体上，本文计算的颤振边界相对于实验值的偏差<2%。

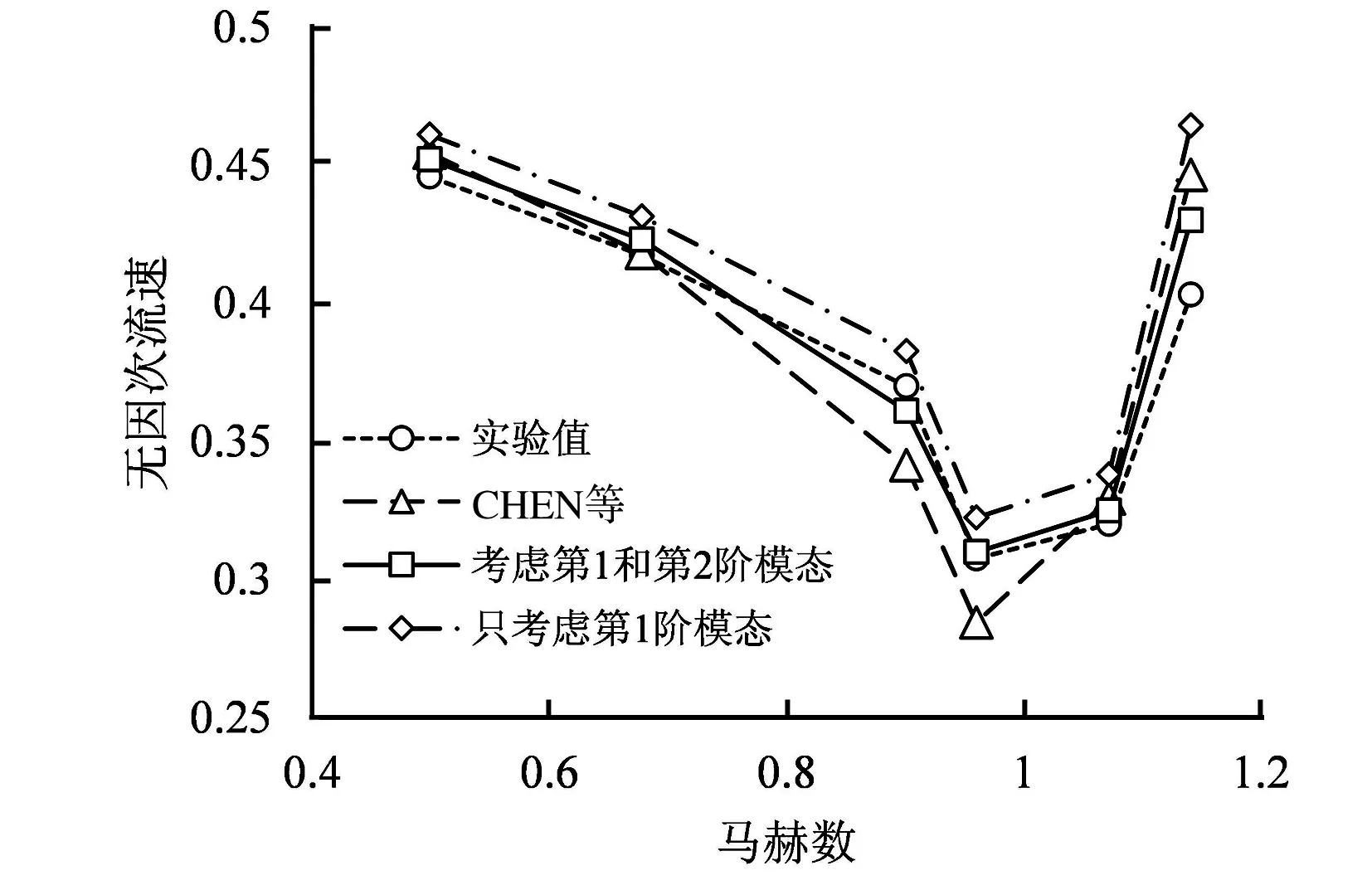
图11 AGARD Wing 445.6 颤振边界Fig.11 Flutter boundary of the AGARD Wing 445.6

6 结 论

本文发展了一种动网格降阶算法，可以实现流固耦合计算中机翼流场网格节点位移的快速计算。采用该方法对AGARD Wing 445.6颤振边界进行了预测，得出如下结论:

(1)采用本文的动网格方法计算出的机翼颤振边界与实验测量得到的颤振边界吻合。

(2)通过与CHEN等计算出的颤振边界比较，发现对于跨音速颤振的预测，Spalart-Allamras湍流模型比Baldwin-Lomax湍流模型的准确性好。

(3)采用RANS方程作为流体控制方程，对机翼超音速颤振进行预测会产生较大的偏差。

(4)与已有的弹性体方法相比，本文的方法可以减少计算时间54.8%。

[ 1 ] CRICKMORE P. Nighthawk F-117 stealth fighter[M]. Zenith Imprint, 2003.

[ 2 ] BURNETT E, ATKINSON C,BERANEK J, et al. NDOF Simulation model for flight control development with flight test correlation[C]//AIAA Modeling and Simulation Technologies Conference. Toronto：American Institute of Aeronautics and Astronautics, 2010: 7780-7794.

[ 3 ] SCHUSTER D M, LIU D D, HUTTSELL L J. Computational aeroelasticity: success, progress, challenge[J]. Journal of Aircraft, 2003, 40(5): 843-856.

[ 4 ] ALBANO E,RODDEN W P. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows[J]. AIAA Journal, 1969, 7(2): 279-285.

[ 5 ] ASHLEY H. Piston theory-a new aerodynamic tool for the aeroelastician[J]. Journal of the Aeronautical Sciences (Institute of the Aeronautical Sciences), 1956, 23(12): 1109-1118.

[ 6 ] YURKOVICH R N, LIU D D, CHEN P C. The state-of-the-art of unsteady aerodynamics for high performance aircraft[C]//39th Aerospace Sciences Meeting and Exhibit. Reno：AIAA, 2001.

[ 7 ] 谢亮, 徐敏, 李杰, 等. 基于 CFD/CSD 耦合的颤振与动载荷分析方法[J]. 振动与冲击, 2012, 31(3): 106-110. XIE Liang, XU Min, LI Jie, et al. Flutter and dynamic analysis based on CFD/CSD coupling method [J]. Journal of Vibration and Shock, 2012, 31(3): 106-110.

[ 8 ] KEYE S. Fluid-structure coupled analysis of a transport aircraft and flight-test validation[J]. Journal of Aircraft, 2011, 48(2): 381-390.

[ 9 ] CHEN X,ZHA G C, YANG M T. Numerical simulation of 3D wing flutter with fully coupled fluid-structural interaction[J]. Computers & Fluids, 2007, 36(5): 856-867.

[10] 史爱明, 杨青, 杨永年. 非结构运动网格下的三维机翼颤振数值分析[J]. 振动与冲击, 2006, 24(6): 27-28. SHI Aiming, YANG Qing, YANG Yongnian. Numerical flutter analysis of a 3D wing using unstructured dynamic mesh Euler method [J]. Journal of Vibration and Shock, 2006, 24(6): 27-28.

[11] TEZDUYAR T E. Stabilized finite element formulations for incompressible flow computations[J]. Advances in Applied Mechanics, 1991, 28: 1-44.

[12] 陈炎, 曹树良, 梁开洪, 等. 基于温度体模型的动网格生成方法及在流固耦合振动中的应用[J]. 振动与冲击, 2010, 29(4): 1-5. CHEN Yan, CAO Shuliang, LIANG Kaihong, et al. A new dynamic grids based on temperature analogy and its application in vibration engineering with fluid-solid interaction [J]. Journal of Vibration and Shock, 2010, 29(4): 1-5.

[13] 谢亮, 徐敏, 张斌, 等. 基于径向基函数的高效网格变形算法研究[J]. 振动与冲击, 2013, 32(10): 141-145. XIE Liang, XU Min, ZHANG Bin, et al. Space points reduction in grid deforming method based on radial basis functions [J]. Journal of Vibration and Shock, 2013, 32(10): 141-145.

[14] BOTTASSO C L, DETOMI D, SERRA R. The ball-vertex method: a new simple spring analogy method for unstructured dynamic meshes [J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(39): 4244-4264.

[15] BAR-YOSEPH P Z, MEREU S, CHIPPADA S, et al. Automatic monitoring of element shape quality in 2D and 3D computational mesh dynamics [J]. Computational Mechanics, 2001, 27(5): 378-395.

[16] STEIN K, TEZDUYAR T, BENNEY R. Mesh moving techniques for fluid-structure interactions with large displacements[J]. Journal of Applied Mechanics, 2003, 70(1): 58-63.

[17] HUO S H, WANG F S, YAN W Z, et al. Layered elastic solid method for the generation of unstructured dynamic mesh[J]. Finite Elements in Analysis and Design, 2010, 46(10): 949-955.

[18] SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flows[C]//30th Aerospace Sciences Meeting and Exhibit.Reno：AIAA,1992.

[19] ZIENKIEWICZ O C, TAYLOR R L, FOX D D. The finite element method for solid and structural mechanics[M]. Amsterdam:Elsevier, 2005：563-588.

[20] LIVNE E, WEISSHAAR T A. Aeroelasticity of nonconventional airplane configurations-past and future[J]. Journal of Aircraft, 2003, 40(6): 1047-1065.

[22] YATES J R,CARSON E. AGARD standard aeroelastic configurations for dynamic response I-wing 445.6[R]. France:Advisory Group for Aerospace Research and Development Neuilly-Sur-Seine,1988.

[23] BEAUBIEN R J, NITZSCHE F, FESZTY D. Time and frequency domain flutter solutions for the AGARD 445.6 wing[C]//International Forum on Aeroelasticity and Structural Dynamics.Munich：CAI, 2005.

[24] RUMSEY C L, SANETRIK M D, BIEDRON R T, et al. Efficiency and accuracy of time-accurate turbulent Navier-Stokes computations[J]. Computers & Fluids, 1996, 25(2): 217-236.

[25] IM H S, CHEN X Y, ZHA G C. Prediction of a supersonic wing flutter boundary using a high fidelity detached eddy simulation[C]//56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference.Florida：AIAA, 2012: 9-12.

Wing flutter prediction using a reduced dynamic mesh method

ZHONGJize,XUZili

(State Key Laboratory for Strength and Vibration of Mechanical Structures,Xi’an Jiaotong University, Xi’an 710049, China)

In this paper, a reduced method for flow mesh deformation around a wing was developed based on the elastic solid method. The flow mesh domain was assumed to be a pseudo elastic solid. The total vibration equation for the wing with the pseudo elastic solid together was derived using the static equilibrium equation of the pseudo elastic solid and the vibration equation of the wing. The nodal displacements for the wing and flow mesh were computed through modal superposition and the deformed flow mesh was obtained. Considering that wing flutter often appeared as the 1stbending and torsion flutter, the nodal displacements for the flow mesh could be calculated by modal superposition of the 1stbending and torsion mode. To ensure the computational accuracy, the 2ndbending and torsion mode were also considered. The flutter boundary of the AGARD Wing 445.6 was predicted using the present dynamic mesh method coupled with the RANS equations and the Spalart-Allamras turbulent model. The relative error of the calculated results to the experimental data was less than 2%. The computing time was reduced by 54.8% compared with the pre-existing elastic solid method.

wing flutter; fluid structure interaction; dynamic mesh; pseudo elastic solid; modal superposition

国家自然基金(51275385);国家973(2011CB706505)

2015-10-19 修改稿收到日期：2016-01-16

仲继泽 男，博士生，1988年7月生

徐自力 男，博士，教授，1967年3月生

V211.3; O327

A

10.13465/j.cnki.jvs.2017.04.029