主被动混合压电网络悬臂梁结构的建模与比较

李明明， 黄春蓉， 方 勃， 段 磊

(1.北京机械设备研究所，北京 100854；2.中国人民解放军驻航天二院二O六所军事代表室，北京 100854；3.哈尔滨工业大学 航天学院，哈尔滨 150001)

主被动混合压电网络悬臂梁结构的建模与比较

李明明1， 黄春蓉2， 方 勃3， 段 磊1

(1.北京机械设备研究所，北京 100854；2.中国人民解放军驻航天二院二O六所军事代表室，北京 100854；3.哈尔滨工业大学 航天学院，哈尔滨 150001)

以Euler-Bernoulli悬臂梁作为研究对象，对主被动混合压电网络(Active-Passive Hybrid Piezoelectric Network, APPN)进行分析与优化。利用Hamilton原理和Rayleigh-Ritz法建立集成式和分离式APPN悬臂梁结构的动力学模型，并对APPN中的电阻和电感进行参数优化。在此基础上，利用速度反馈控制设计主动控制器，分别对集成式和分离式APPN悬臂梁结构的开环和闭环特性进行数值仿真分析。仿真结果表明，两种结构形式的APPN均能够有效地抑制结构振动，集成式APPN在窄频带的振动控制性能优于纯主动控制，而分离式APPN则在更宽的频带具有比集成式APPN和纯主动控制更好的振动控制性能。

主被动混合压电网络；Euler-Bernoulli悬臂梁；Hamilton原理；Rayleigh-Ritz法；速度反馈控制

压电材料具有正、逆压电效应，它既能将机械能转化为电能，又能将电能转化为机械能。由压电材料制成的作动器、传感器和换能器已经广泛应用于结构主动振动控制和被动振动控制中[1-5]。在压电主动控制系统中，粘贴于结构表面或嵌入结构内部的压电作动器与反馈控制系统相连，结构振动时，传感器检测到的振动信号通过反馈控制系统后输出控制电压，驱动压电作动器对结构振动进行实时控制；在压电被动控制系统中，压电材料与外部分流电路相连，结构振动时，部分机械能由于压电材料的正压电效应转化为电能，并通过分流电路中的阻抗转化为焦耳热，从而达到耗散系统总能量、抑制结构振动的目的。

由于压电主动控制和压电被动控制的作用机理不同，因此两种振动控制方法的特点也不同。与压电被动控制相比，压电主动控制具有更好的控制性能、更宽的控制频带和更强的环境适应性，但是压电主动控制需要外界能源、结构较复杂、可靠性和稳定性较差；而压电被动控制则具有不需要外界能源、结构简单、易于实现、可靠性高等优点，尽管压电被动控制的环境适应性较差。AGNES[6]结合压电主动控制和压电被动控制各自的特点，提出一种主被动混合压电网络(Active-Passive Hybrid Piezoelectric Network, APPN)用于结构振动控制，如图1所示。在APPN中，压电层既能够通过反馈控制电压主动地控制结构振动，又能够通过分流电路被动地耗散结构振动的能量，使得APPN兼具主动控制和被动控制两方面的优点，因而得到了国内外学者的广泛关注[7-13]。

TSAI等[8]利用APPN对环形结构进行了振动控制，研究表明，APPN能够有效地抑制结构振动与噪声。与纯主动控制相比，APPN只需要较小的控制电压，即可获得更好的振动控制性能。随后ZHAO[9]和GODOY等[10]利用APPN对四边形板和复合材料层合板进行了振动控制。TANG等[11]在研究APPN时，考虑到压电材料具有高阶非线性和迟滞特性，采用滑模控制理论设计了鲁棒控制器，以补偿系统的非线性和不确定性。在上述研究中，APPN的结构形式均为集成式，TSAI等[12]还提出一种分离式APPN(如图2所示)，并且对两种APPN进行了比较。通过比较两种APPN在第一阶主模态的主动控制权益，TSAI等发现集成式APPN比分离式APPN具有更好的振动控制性能。

本文以Euler-Bernoulli悬臂梁作为研究对象，利用Hamilton原理和Rayleigh-Ritz法分别建立集成式和分离式APPN悬臂梁结构的动力学模型，并对APPN中的电阻和电感进行参数优化。通过在宽频带内对APPN悬臂梁结构进行开环和闭环特性分析，更全面地考查集成式APPN和分离式APPN所具有的振动控制性能，得到一些新的结论。

1 结构形式与基本假设

1.1 结构形式

集成式和分离式APPN悬臂梁结构如图1和图2所示，其中RL电路为分流电路。为了使两种APPN悬臂梁在结构上保持一致，本文在集成式APPN悬臂梁结构中增加了配重压电层。

图1 集成式APPN悬臂梁Fig.1 Cantilever beam with integrated APPN treatment

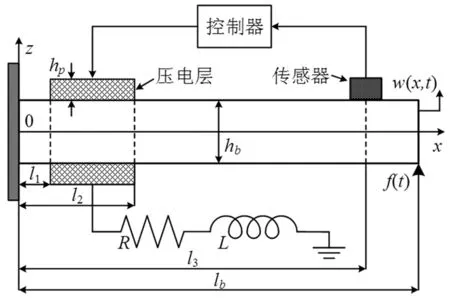
图2 分离式APPN悬臂梁Fig.2 Cantilever beam with separated APPN treatment

1.2 基本假设

在建立APPN悬臂梁结构的动力学模型之前，首先进行如下处理和假设：

(1)假设悬臂梁为Euler-Bernoulli悬臂梁，由此可知悬臂梁及其上的压电层在电场强度为零时的正应力和正应变分别为

σb=Ebεb

(1)

σp=Epεp

(2)

(3)

式中:Eb和Ep分别为悬臂梁和压电层的弹性模量。

(2)假设压电层的极化方向沿其厚度方向向上(即沿z轴正方向)，且压电层的电场强度e(t)表示为[14]

(4)

式中:va(t)和vs(t)分别为悬臂梁上、下压电层表面上的电压；hb和hp分别为悬臂梁和压电层的厚度。

(3)利用Rayleigh-Ritz法，将悬臂梁的横向位移w(x,t)表示为

(5)

式中:φi(x)为假设的模态函数，ri(t)为相应的广义坐标，上角标T为矩阵或向量的转置。由振动力学可知，

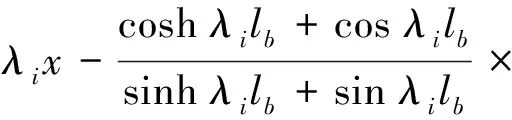
(sinhλix-sinλix) (i=1,2,…,n)

(6)

式中:lb为悬臂梁的长度，λi则由下式确定

cosλilbcoshλilb=-1

(7)

2 动力学建模

下面利用Hamilton原理建立APPN悬臂梁结构的动力学模型。从分析力学中知道，Hamilton原理的广义形式为[15]

(8)

式中:Tk为动能，U为势能，We为电能，δW为外力所作的虚功。

2.1 集成式APPN悬臂梁结构建模

集成式APPN悬臂梁结构的动能表示为

(9)

式中:Vb和Vp分别为悬臂梁和压电层的体积；ρb和ρp分别为悬臂梁和压电层的密度。将式(5)代入式(9)，整理得

(10)

式中各质量阵的表达式为

式中:l1和l2为压电层左、右两端到悬臂梁固定端的距离；b为悬臂梁和压电层的厚度。

集成式APPN悬臂梁结构的势能表示为

(11)

式中第二项为悬臂梁上表面压电层的势能，第三项为下表面配重压电层的势能。

对于一维结构来说，压电材料的本构方程为[16]

(12)

(13)

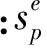
(14)

将式(5)代入式(14)，整理得

(15)

式中各刚度阵的表达式为

集成式APPN悬臂梁结构的电能表示为

(16)

将式(13)、式(3)、式(4)代入式(16)得

(17)

将式(5)代入式(17)，整理得

(18)

式中:Cp=bξε(l2-l1)/hp。

从图1中可以看到，集中力f(t)作用于x=lb处，并且考虑悬臂梁为有阻尼梁，则外力所作的虚功表示为

q(t)δva(t)

(19)

式中:δ*(x)为Dirac delta函数，cb为阻尼系数，q(t)为压电层上的电荷量。将式(5)代入式(19)，整理得

(20)

其中载荷系数矩阵和阻尼阵的表达式为

将式(10)、式(15)、式(18)和式(20)代入式(8)，整理得

(21)

ΘTr(t)+Cpva(t)=q(t)

(22)

式中:M=Mb+Mp，K=Kb+Kp。

由于压电层、RL电路和控制器串联(如图1所示)，因此该串联电路的电压关系为[11]

(23)

式中:vin(t)为控制电压，R和L分别为电阻和电感。将式(22)分别代入式(21)和式(23)，得集成式APPN悬臂梁结构的动力学模型为

(24)

(25)

2.2 分离式APPN悬臂梁结构建模

对比图1和图2可以看出，集成式和分离式APPN悬臂梁结构的最大区别在于两个压电层的作用不同。

在集成式APPN悬臂梁结构中，上表面压电层既要作为作动器对结构振动进行实时控制，又要作为换能器将结构振动的能量转化为电能并通过RL电路耗散掉；而在分离式APPN悬臂梁结构中，上表面压电层作为作动器，下表面压电层作为换能器。

因此，分离式APPN悬臂梁结构的动能和外力所作的虚功与集成式相同，仅需要对势能和电能的表达式进行适当修改。

对式(14)进行适当修改，得分离式APPN悬臂梁结构的势能表达式为

(26)

将式(5)代入式(26)，整理得

(27)

而分离式APPN悬臂梁结构的电能表示为

(28)

式中:第一项为悬臂梁上表面压电层的电能，第二项为下表面压电层的电能。将式(13)、式(3)、式(4)代入式(28)得

(29)

将式(5)代入式(29)，整理得

(30)

将式(10)、式(27)、式(30)和式(20)代入式(8)，整理得

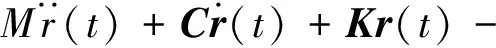
Θva(t)-Θvs(t)=Ff(t)

(31)

ΘTr(t)+Cpvs(t)=q(t)

(32)

考虑到下表面压电层与RL电路相连，因此该串联电路的电压关系为

(33)

将式(32)分别代入式(31)和式(33)，并已知va(t)=vin(t)，得分离式APPN悬臂梁结构的动力学模型为

(34)

(35)

3 参数优化

研究表明，RL电路的减振机理与有阻尼动力吸振器相同，电阻R和电感L只对结构的某一阶主模态具有最优值。因此，当vin(t)=0时，集成式和分离式APPN悬臂梁结构的动力学模型简化为

(36)

(37)

采用与有阻尼动力吸振器相同的优化方法对RL电路进行参数优化[7]，可得电阻和电感的最优值分别为

(38)

4 开环和闭环特性分析

已知位移传感器位于x=l3处，用于测量悬臂梁的位移响应，所以APPN悬臂梁结构的传感方程可表示为

(39)

另外假设集中力f(t)为简谐激振力

f(t)=f0sinωt

(40)

式中:f0为激振力幅值，ω为激振力角频率。

4.1 开环特性分析

定义w1(l3,t)/f(t)为激振力与位移响应之间的传递函数，w2(l3,t)/vin(t)为控制电压与位移响应之间的传递函数，其中w1(l3,t)、w2(l3,t)分别为激振力和控制电压单独作用时引起的位移响应。再定义T1和T2为w1(l3,t)/f(t)和w2(l3,t)/vin(t)的幅值，由此可知，T1表示被动阻尼性能，其越小越好；T2表示主动控制权益，其越大越好。

对于集成式APPN悬臂梁结构，T1和T2的表达式为

(41)

(42)

其中

对于分离式APPN悬臂梁结构，T1和T2的表达式为

(43)

(44)

比较式(41)、式(42)与式(43)、式(44)可以看出，集成式和分离式APPN悬臂梁结构具有相同的被动阻尼性能表达式，不同的主动控制权益表达式。这是由于，当忽略主动控制时，二者的结构形式完全相同，因而具有相同的被动阻尼性能；当考虑主动控制时，集成式APPN悬臂梁结构的控制电压通过RL电路输入到压电层上，分离式APPN悬臂梁结构的控制电压就是压电层上的电压，因而具有不同的主动控制权益。

下面对APPN悬臂梁结构进行数值仿真分析。由于悬臂梁作为连续体具有无穷多个主模态，为了研究方便，本文选取前二阶主模态对APPN悬臂梁结构的开环和闭环特性进行分析。APPN悬臂梁结构的具体参数如表1所示。根据上述参数求得，控制第一阶主模态振动的最优电阻和电感值分别为R1=16.98 kΩ，L1=214.15 H；而控制第二阶主模态振动的最优电阻和电感值分别为R2=1.55 kΩ，L2=8.41 H。

当选择R1和L1对悬臂梁第一阶主模态进行振动控制时，从图3中可以看出，APPN能够有效控制第一阶主模态的振动，但是无法控制第二阶主模态的振动。

当选择R2和L2对悬臂梁第二阶主模态进行振动控制时，从图4中可以看出，APPN能够有效控制第二阶主模态的振动，但是对第一阶主模态的振动控制效果并不显著。

从图3和图4中可以看出，由于选择最优的电阻和电感对悬臂梁第一阶主模态或第二阶主模态进行振动控制，导致APPN只对悬臂梁第一阶主模态或第二阶主模态具有显著的振动控制作用，而对其它阶主模态无法实施有效的控制。但是APPN并非只能控制悬臂梁某一阶主模态的振动，如图5所示，当选择R=25 kΩ、L=1 H时，APPN能够同时控制悬臂梁前二阶主模态的振动。但无论选择怎样的电阻和电感值，无非是将APPN的振动控制性能进行了折中，却无法使APPN的振动控制性能在前二阶主模态同时达到最优。

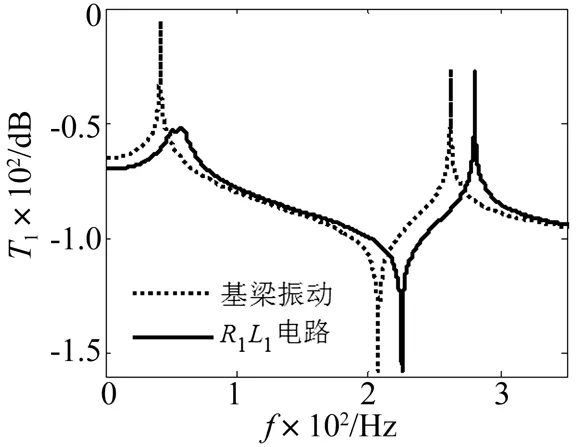
图3 被动阻尼性能(R1L1电路)Fig.3 Passive damping performance with R1L1 circuit

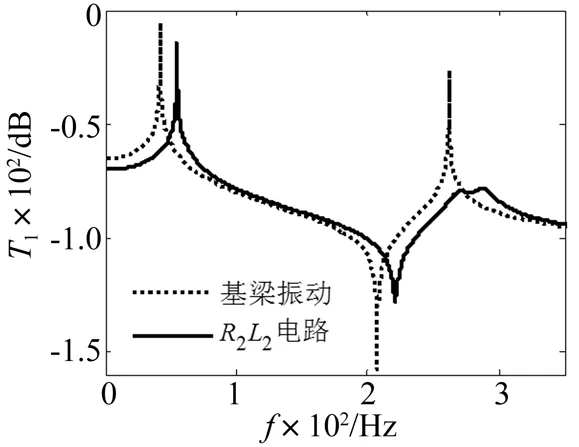
图4 被动阻尼性能(R2L2电路)Fig.4 Passive damping performance with R2L2 circuit

参数数值参数数值l1/mm10l2/mm50l3/mm180lb/mm200hb/mm2hp/mm0．8b/mm30c/(N·s·m-2)0．13ρb/(kg·m-3)7850ρp/(kg·m-3)7500Eb/GPa210Ep/GPa60．6d31/(pm·V-1)-274ξε/(nF·m-1)25．55

TANG等[17]亦对RL电路进行了参数优化，得到最优电阻和电感值的表达式为

(45)

利用式(45)求得控制第一阶主模态振动的最优电阻和电感值分别为R1=19.61 kΩ，L1=214.15 H；而控制第二阶主模态振动的最优电阻和电感值分别为R2=1.55 kΩ，L2=8.41 H。通过对两种优化方法进行数值比较可以看出(如图6所示)，利用式(38)求得的最优电阻和电感值可以使APPN具有更好的被动阻尼性能。

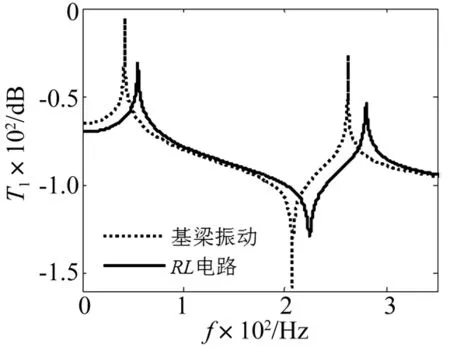
图5 被动阻尼性能(R=25 kΩ，L=1 H)Fig.5 Passive damping performance with R=25 kΩ, L=1 H

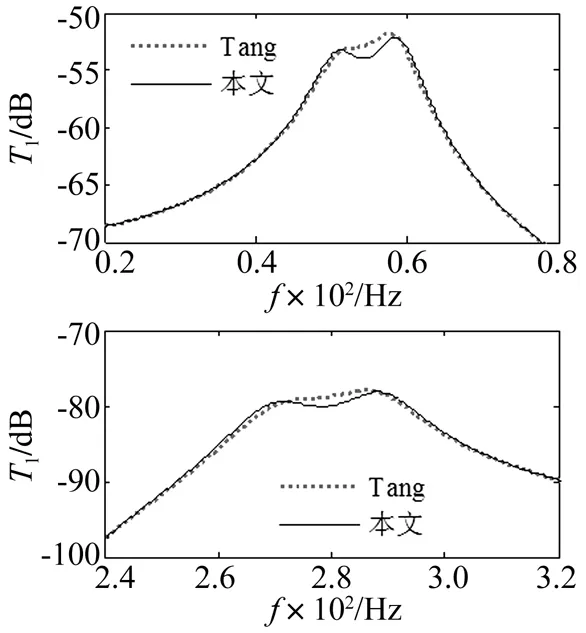
图6 优化方法比较Fig. 6 Comparison of optimization methods

图7对两种APPN的主动控制权益进行了比较。从图中可以看出，当选择R1和L1对悬臂梁第一阶主模态进行振动控制时，在一阶共振频率附近，分离式APPN的主动控制权益小于集成式APPN和纯主动控制的主动控制权益(这一结论与TSAI等[12]得出的结论是相同的)；但是在二阶共振频率附近，分离式APPN的主动控制权益与纯主动控制几乎是相同的，二者均明显优于集成式APPN的主动控制权益。

4.2 闭环特性分析

为了研究方便，本文采用速度反馈控制设计主动控制器，因此控制电压表示为

(46)

式中:Kc=1 500为反馈控制增益。将式(39)代入式(46)得

(47)

定义w(l3,t)/f(t)为激振力与位移响应之间的闭环传递函数，并令T3为w(l3,t)/f(t)的幅值，由此可知，T3表示系统的闭环控制性能，其越小越好。

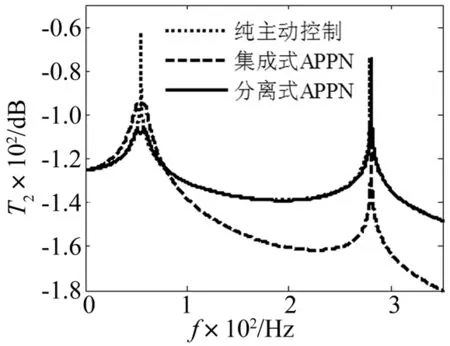
图7 主动控制权益Fig.7 Active control authority

对于集成式APPN悬臂梁结构，T3的表达式为

(48)

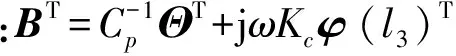
对于分离式APPN悬臂梁结构，T3的表达式为

T3=

(49)

当选择R1和L1对悬臂梁第一阶主模态进行振动控制时，从图8中可以看出，在一阶共振频率附近，集成式APPN的振动控制性能优于分离式APPN和纯主动控制；但是在二阶共振频率附近，集成式APPN的振动控制性能远不及分离式APPN和纯主动控制。

下面结合图3和图7对这一结果进行阐释。从图3中可以看出，通过R1L1电路对悬臂梁施加的被动控制，已经使APPN为悬臂梁第一阶主模态提供了很大的被动阻尼，因此，尽管集成式和分离式APPN在一阶共振频率附近的主动控制权益远小于纯主动控制(如图7所示)，还是使集成式和分离式APPN具有比纯主动控制更好的闭环控制性能(如图8所示)。但是对于第二阶主模态，R1L1电路未提供被动阻尼，而且集成式APPN的主动控制权益也远不及分离式APPN和纯主动控制，因此，集成式APPN在二阶共振频率附近的振动控制性能亦远不及分离式APPN和纯主动控制。另一方面，由于分离式APPN在二阶共振频率附近的主动控制权益与纯主动控制相当，使得二者的闭环控制性能亦相同。

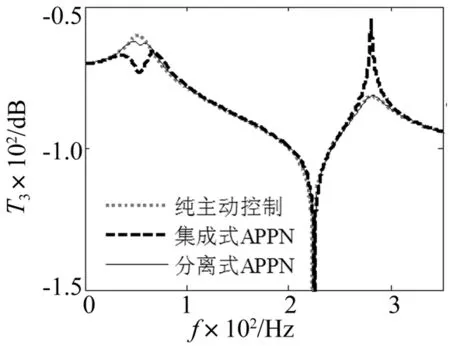
图8 闭环控制性能(R1L1电路)Fig.8 Closed-loop control performance with R1L1 circuit

4.3 纯主动控制、集成式APPN和分离式APPN的比较

利用上述分析结果，可以对纯主动控制、集成式APPN和分离式APPN进行如下比较：

首先，纯主动控制不具有被动阻尼性能，若反馈控制系统出现故障可能会造成系统失稳；而集成式和分离式APPN均具有很好的被动阻尼性能(且二者的被动阻尼性能完全相同)，这在一定程度上增加了系统的稳定裕度。

其次，当选择R1和L1对悬臂梁第一阶主模态进行振动控制时，集成式APPN的闭环控制性能在一阶共振频率附近优于分离式APPN和纯主动控制，在二阶共振频率附近则远不及分离式APPN和纯主动控制；而分离式APPN在一阶和二阶共振频率附近均具有良好的闭环控制性能(如图8所示)。

由此可知，集成式APPN在窄频带的振动控制性能优于分离式APPN和纯主动控制，而分离式APPN则在更宽的频带具有比集成式APPN和纯主动控制更好的振动控制性能。

事实上，即使未对APPN中的RL电路进行参数优化，分离式APPN依然具有比纯主动控制更好的振动控制性能。例如，当选择R=25 kΩ、L=1H对悬臂梁进行振动控制时，从图5和图9中可以看出，分离式APPN不仅具有与纯主动控制相当的闭环控制性能，还具有纯主动控制所没有的良好的被动阻尼性能。也就是说，即使分离式APPN的主动控制部分出现故障，其被动控制部分依然能够起到很好的抑制振动的作用。

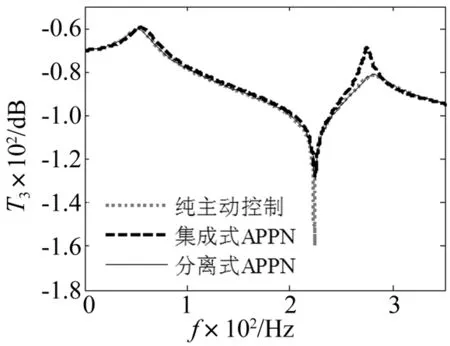
图9 闭环控制性能(R=25 kΩ，L=1 H)Fig.9 Closed-loop control performance with R=25 kΩ, L=1 H

5 结 论

本文以Euler-Bernoulli悬臂梁作为研究对象，利用Hamilton原理和Rayleigh-Ritz法建立集成式和分离式APPN悬臂梁结构的动力学模型，通过对APPN悬臂梁的开环和闭环特性进行深入研究，得到了如下结论：

(1)集成式APPN和分离式APPN具有相同的被动阻尼性能、不同的主动控制权益，从而导致二者具有不同的闭环控制性能。

(2)采用与有阻尼动力吸振器相同的优化方法可以对APPN中的RL电路进行参数优化，但是利用这种方法得到的最优电阻和电感值只能使APPN在某一阶主模态具有最优的被动阻尼性能，而无法使APPN的被动阻尼性能在各阶主模态同时达到最优。

(3)由数值仿真结果可知，集成式APPN在窄频带的振动控制性能优于分离式APPN和纯主动控制，而分离式APPN则在更宽的频带具有比集成式APPN和纯主动控制更好的振动控制性能。

[ 1 ] LI F M, LYU X X. Active vibration control of lattice sandwich beams using the piezoelectric actuator/sensor pairs[J]. Com-posites: Part B, 2014, 67: 571-578.

[ 2 ] GAO L, LU Q Q, FEI F, et al. Active vibration control based on piezoelectric smart composite[J]. Smart Materials and Struc-tures, 2013, 22(12): 125032.

[ 3 ] ZHANG S Q, SCHMIDT R, QIN X S. Active vibration control of piezoelectric bonded smart structures using PID algorithm[J]. Chinese Journal of Aeronautics, 2015, 28(1): 305-313.

[ 4 ] CASADEI F, BECK B S, CUNEFARE K A, et al. Vibration control of plates through hybrid configurations of periodic piezoelectric shunts[J]. Journal of Intelligent Material Systems and Struc-tures, 2012, 23(10): 1169-1177.

[ 5 ] JEON J Y. Passive vibration damping enhancement of piezo-electric shunt damping system using optimization approach[J]. Journal of Mechanical Science and Technology, 2009, 23(5): 1435-1445.

[ 6 ] AGNES G S. Development of a modal model for simultaneous active and passive piezoelectric vibration suppression[J]. Jour-nal of Intelligent Material Systems and Structures, 1995, 6(4): 482-487.

[ 7 ] LI M M, FANG B, CAO D Q, et al. Modeling and analysis of cantilever beam with active-passive hybrid piezoelectric net-work[J]. Science China: Technological Sciences, 2013, 56(9): 2326-2335.

[ 8 ] TSAI M S, WANG K W. Control of a ring structure with multiple active-passive hybrid piezoelectrical networks[J]. Smart Mate-rials and Structures, 1996, 5(5): 695-703.

[ 9 ] ZHAO Y H. Vibration suppression of a quadrilateral plate using hybrid piezoelectric circuits[J]. Journal of Vibration and Con-trol, 2010,16(5): 701-720.

[10] GODOY T C, TRINDADE M A. Modeling and analysis of laminate composite plates with embedded active-passive piezoelectric networks[J]. Journal of Sound and Vibration, 2011, 330(2): 194-216.

[11] TANG J, WANG K W, PHILEN M. Sliding mode control of struc-ture vibrations via active-passive hybrid piezoelectric network [C]// Wereley N W. Proceedings of SPIE, Newport Beach, CA: SPIE, 1999, 3668: 543-554.

[12] TSAI M S, WANG K W. On the structural damping characteris-tics of active piezoelectric actuators with passive shunt[J]. Journal of Sound and Vibration, 1999, 221(1): 1-22.

[13] MOON S H, KIM S J. Suppression of nonlinear composite panel flutter with active/passive hybrid piezoelectric networks using finit element method[J]. Composite Structures, 2003, 59(4): 525-533.

[14] HAGOOD N W, CHUNG W H, FLOTOW A V. Modelling of piezoele-ctric actuator dynamics for active structural control[J]. Journal of Intelligent Material Systems and Structures, 1990, 1(3): 327-354.

[15] DUTOIT N E, WARDLE B L, KIM S G. Design considerations for MEMS-scale piezoelectric mechanical vibration energy harve-sters[J]. Integrated Ferroelectrics, 2005, 71(1): 121-160.

[16] DIETL J M, GARCIA E. Beam shape optimization for power har-vesting[J]. Journal of Intelligent Material Systems and Struc-tures, 2010, 21(6): 633-646.

[17] TANG J, WANG K W. Active-passive hybrid piezoelectric net-works for vibration control:comparisons and improvement[J]. Smart Materials and Structures, 2001, 10(4): 794-806.

Modelling and comparison of cantilever beams withan active-passive hybrid piezoelectric network

LI Mingming1, HUANG Chunrong2, FANG Bo3, DUAN Lei1

(1. Beijing Mechanical Equipment Institute, Beijing 100854, China；2.Military Representative Office at No. 206 Institute of the Aerospace Second Academy, Beijing 100854, China；3.School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)

Taking an Euler-Bernoulli cantilever beam as the study object, active-passive hybrid piezoelectric network (APPN) was analyzed and optimized. Hamilton’s principle and Rayleigh-Ritz method were used to build the dynamic models of the cantilever beam with integrated and separated APPNs, respectively. Parametric optimization was performed for resistance and inductance in the APPN. Furthermore, the velocity feedback control was employed to design the active controller and the open-loop and closed-loop characteristics of the cantilever beams with integrated and separated APPNs, respectively were simulated andn analyzed. The numerical results showed that both integrated and separated APPNs can suppress the structures’ vibrations effectively; compared with the pure active control, the integrated APPN has a better vibration control performance in narrow frequency bands, while the separated APPN has a better vibration control performance in broader frequency bands than both the integrated APPN and the pure active control do.

active-passive hybrid piezoelectric network; Euler-Bernoulli cantilever beam; Hamilton’s principle; Rayleigh-Ritz method; velocity feedback control

国家自然科学基金(11402087)

2015-11-03 修改稿收到日期：2016-01-18

李明明 男，博士，工程师，1982年10月生

方勃 男，博士，教授，1964年8月生

O328

A

10.13465/j.cnki.jvs.2017.03.016