基于关联度的线控交叉口间距确定方法研究
2017-03-08施群
施 群
(福建农林大学金山学院 工程技术系,福建 福州 350002)
合理的交叉口信号配时方案与渠化设计措施有利于提高城市道路通行能力、缓解交通拥挤、降低交通事故等。其中,干道信号协调控制系统的普及与合理应用更是城市道路网信号控制系统发展的必然趋势。在对路网中若干连续交叉口实行信号的协调控制时,需要根据各交叉口之间的相关程度分区并分别制定配时方案。根据交叉口相关性强弱,路网可化整为零,划分为若干个独立子区域,并分别设置信号配时方案,以便更灵活地执行控制策略获得最佳控制效果。与此同时,综合考虑交叉口安全因素,提出适用于干线协调控制的交叉口间距确定方法具有一定工程意义。
1 交叉口关联性分析
1.1 影响因素
交叉口关联性的主要影响因素有交叉口间距、交通流量、信号周期时长,其影响关系如图1所示。

图1 交叉口关联程度与其影响因素的关系
其中,交叉口间距作为静态影响因子对交叉口关联性的影响是固定不变的;而交通流量、信号周期时长对交叉口关联性强弱的影响是时时改变的。
(1)交叉口间距
交叉口间距越大其相关性越弱,反之,交叉口间距越小其相关性越强。
(2)交通流量
交通流量作为道路截面实际通行能力的测算指标,其大小将直接决定路段交通拥堵程度。交通量越大交叉口相关性越强,反之,交通量越小交叉口相关性越弱。
(3)信号周期时长
相邻干道交叉口间设置整齐的信号周期与稳定的相位差,可使交叉口间的协调效果更优。交叉口之间的信号周期比值越整齐则交叉口之间的关联程度越大。
1.2 计算模型
交叉口关联性是动态变化的,并且能够实时反映城市道路网络交通流的时空变化。交叉口间关联性的定量化分析有助于其信号协调方案的选取。因此,引入交叉口关联度这一指标作为交叉口实行信号协调控制的优先级判断依据。其中,交叉口关联度是离散性关联度和阻滞性关联度两个指标的综合值[1]。
(1)离散性关联度计算模型
离散性关联度指在干线网中一个信号周期内,某一路径终点与起点的通过交通量比值。其计算式为:
(1)
式中:qd(i+T)—第i+T个时段到达路径末端交叉口的交通量(pcu);
q0(i)—第i个时段通过路径起点上游交叉口停止线的交通量(pcu);
T—路径起讫点间车辆行驶时间(s);
tg—绿灯时长(s)。
理论计算中,q0(i)采用路段实测值,qd(i+T)则通过Robertson车队离散公式进行计算。其具体公式为:
(2)
F=1/(1+αt)
(3)
t=βT=β(j-i)
(4)
式中:q0(j)—第j个时段通过路径末端上游交叉口停止线的交通量(pcu);
α—标定参数,取0.35;
β—标定参数,取0.8。
车队行驶离散性是影响干线协调控制实施效果的重要因素之一,主要表现为车队在运动过程中首车与尾车之间的距离逐渐加大,以致整个车队通过下游交叉口停车线所需的时间加长。在进行干线协调控制设计时,应充分考虑车队行驶离散性,即尽可能在同一信号周期完成离散车队的放行。根据公式(1)可知,交叉口离散关联度I1是某一路径终点与起点的通过交通量比值。离散关联度取值越大,同一信号周期内完成离散车辆放行的比例就越大。
根据公式(1)~(4)计算可得不同行程车速情况下,离散性关联度与交叉口间距之间的影响关系,如图2所示。
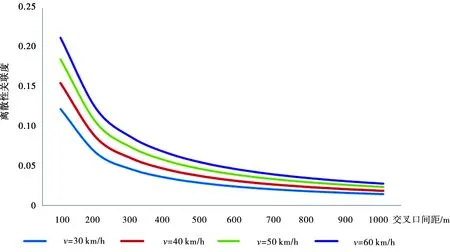
图2 交叉口间距对离散性关联度的影响
由图2可知:交叉口间距越短,离散性关联度越大,则在同一信号周期内离散车辆在下游交叉口完成放行的数量越大。因此,就针对车辆离散特性而言,交叉口间距取值越小,干线协调控制的效益越高。
(2)阻滞性关联度计算模型
由于干线协调控制是针对直行车流进行调控的控制方式,故将阻滞性关联度定义为直行车道上游功能区长度与交叉口间距的比例关系,其计算式为:
(5)
(6)
式中:Lm—第m个路段的交叉口间距(m);
Dm—第m个路段的上游功能区长度(m);
M—交叉口群中组成某一路径的路段数。
根据公式(5)、(6)计算可得不同行程车速情况下,阻滞性关联度与交叉口间距之间的影响关系,如图3所示。

图3 交叉口间距对阻滞性关联度的影响
由图3可知:交叉口间距越短,阻滞性关联度越大,则信号控制对路段起到协调效果的对象所占比例越大,即干线协调效益越好。
(3)交叉口路径关联度
交叉口离散性关联度是对交通流离散性分布的定量描述,阻滞性关联度则是交叉口功能区占所在路段百分比的体现。将路径关联度作为二者的量化指标,其计算公式为:
(7)
式中:I1max、I1min—研究范围内所有路径离散性关联度最大、最小值;
I2max、I2min—研究范围内所有路径阻滞性关联度最大、最小值。
其中,当:I1=I1max、I2=I2max时,路径关联度为0;当I1=I1min、I2=I2min时,路径关联度为2。因此,路径关联度量化后取值区间为[0,2]。对于干线交叉口的信号协调控制设置,可以依据路径关联度的大小进行优先排序,路径关联度量化指标小的路径应予以优先考虑信号协调控制。
2 交叉口合理间距区间确定
基于城市干道交叉口间的交通特性,交叉口间距需设置足够的长度以避免交叉口上、下游交通影响区域的重叠,并且为车辆的分流、合流等行为提供独立且安全的运行空间。而纳入干线协调控制的道路,各相邻交叉口间距要适当才能使之保持较强的关联性。因此,城市干道信号交叉口间距的确定应充分考虑安全与效率。
2.1 最大容许交叉口间距
在信号交叉口中,车流到达特性决定了干线协调控制的协调效益。交通流呈脉冲式的连续交叉口最为适宜设置干道协调控制系统。路段上车辆若单独零星地到达交叉口,干线协调控制系统将较难发挥作用。而车辆若以车队为整体离散地到达交叉口,信号协调控制效果将达到较优水平。此时车辆将以车队形式间断地到达交叉口,而又不至发生二次排队或过饱和状态,协调效益将得以发挥。因此,如何界定车辆离散程度对于干线协调控制效益的影响至关重要。美国《交通控制系统手册》[2]中提出,可根据区域的几何关系、交通量大小、交通流特性参数对信号网进行系统划分,进而选取控制方式与配时方案。研究提出利用互联合理性指数Y,对系统中各道路是否采用干线协调控制系统进行简单划分。互联合理性指数是综合考虑车队离散与道路几何条件等因素的参数,其计算公式为:
(8)
式中:tL—路段行程时间(min);
L—交叉口间距(m);
v—设计车速(km/h);
n—上游交叉口车流转向数(十字交叉口转向数取n=3);
qs—上游交叉口直行交通量(pcu);
qn—上游交叉口各转向交通量(pcu)。
为保证信号协调的交通效益,互联合理性指数应不小于0.35[3]。根据公式(8)计算可得不同行程车速情况下干线协调控制效益较优的最大交叉口间距取值,如表1所示。

表1 干线协调控制交叉口最大容许间距取值表
2.2最小交叉口安全间距
由于城市干道相邻交叉口间距需向区域内行驶车辆提供安全驾驶空间,其最小安全间距的确定将综合考虑交叉口功能区长度、交叉口安全视距及车辆变道所需安全距离。
(1)上游功能区长度
根据车辆在交叉口上游功能区进行的一系列复杂的操作,可将交叉口上游功能区分为感知—反应区域、制动区域、排队区域三个部分。该分区如图4所示。

图4 上游功能区示意图
其长度计算模型为:
D上=d1+d2+d3
(9)
d1=v×t1/3.6
(10)
(11)
(12)
式中:d1—车辆在感知——反应时间内行驶的距离(m);
d2—车辆加速或减速行驶的距离(m);
d3—车辆排队长度(m);
v—车辆行驶速度(km/h),以设计车速代替;
v0—车辆制动初速度,以设计车速代替(km/h);
a—车辆减速度,取为2.5 m/s2;
t1—驾驶员感知反应时间,取值为2.50 s;
t2—车辆制动滞后时间,取为0.6 s;
t3—车辆制动增长时间,取为0.9 s;
t4—线控系统中,下游交叉口绿灯启亮与上游交叉口绿灯启亮的间隔时间(s);
S—平均车头间距,一般取7 m;
L—交叉口间距(m)。
(2)下游功能区长度
下游功能区是指车辆驶离交叉口后,交通行为受制约、影响的区域。基于安全考虑,在这一功能区域内,道路的安全视距应保证以设计车速行驶的车辆在到达前方的固定障碍物前能够安全停车。因此,下游功能区长度计算公式为:
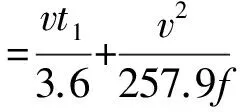
(13)
式中:f—摩擦系数,约等于以重力加速度g为单位的减速度,干燥水平道路上取为0.65。
v,t1—各参数含义同上。
(3)交叉口安全视距
交叉口的每一条进口道都需向车辆提供适宜的引道视距、停车视距、安全交叉停车视距。各种交叉口安全视距如图5所示。
由图5与表2可知:交叉口安全视距(停车视距、引道视距、安全交叉停车视距)均落在交叉口上游功能区的范围之内。因此,若交叉口间距能满足上游功能区长度取值,则必定能满足交叉口安全视距的要求。
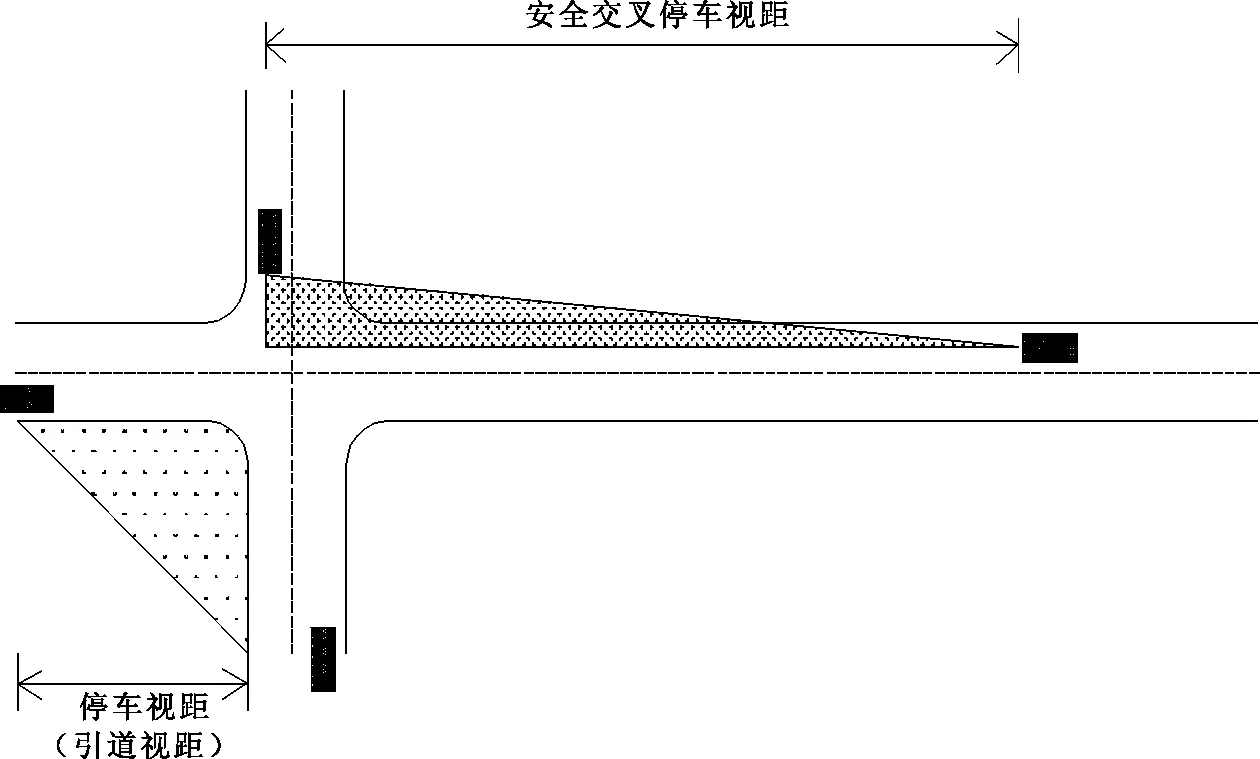
图5 交叉口安全视距示意图
根据《公路路线设计规范》[4]要求,各交叉口安全视距取值如表2所示。

表2 交叉口安全视距取值表
(4)车辆变道所需安全距离
城市干道多为双向多车道,并且存在大量的车辆变换车道行为。车辆变道前,驾驶员需考虑为避免车辆碰撞的车辆间安全距离。为顺利完成这一过程,行驶车辆需要充足的时间与距离。
出于对变道安全性考虑,计算将基于可接受间隙的车辆变道模型展开。车辆变道安全距离包括:等待可插车间隙出现所需时间内行驶的距离L1、调整车速利用可插车间隙所需时间内行驶的距离L2、驾驶员“判断—反应”时间内行驶的距离L3、车辆横向偏移时纵向行驶距离L4。综合各种距离,得出车辆变道所需安全距离为:
(14)
(15)
式中:tw—可插车间隙平均等待时间(s);
v—车辆运行速度(km/h);
vl—换车道速度(km/h);
t5—车辆横向位移时间,取3.0 s;
n—车辆某次变道行为跨越的车道数,通常取1;
tc—可接受间隙临界值,5.0 s[5];
λ—单位时间的车辆平均到达率(pcu/s);
τ—车头时距,取1.889 s[6]。
根据道路空间富余程度,可将信号控制交叉口最小安全间距分为两类:(1)在道路条件允许的情况下,综合考虑满足各种条件要求的安全间距取值的第一类交叉口安全间距;(2)在交叉口长度受限制时至少需提供车辆安全进出交叉口上、下游功能区长度范围的第二类交叉口安全间距。综上所述,不同设计车速情况下的最小交叉口安全间距如表3所示(此处交叉口区域长度暂取60 m)。

表3 交叉口安全间距取值表
3 干道交叉口间距确定方法
3.1 最优路径关联度区间
为兼顾干线协调控制效益与交叉口交通运行安全,交叉口关联度应适中,不宜过大也不能太小。目前,已有相关研究指出可以通过计算交叉口关联度的大小来判断交叉口间需要协调控制的程度。Edmond[7]通过研究车辆离散现象提出交叉口关联度取值的区间为[0,1]。当关联度取值大于等于0.5时,他认为交叉口应进行信号的协调控制;当关联度取值小于0.25时,相邻交叉口不需要进行协调控制;当关联度取值介于0.25~0.5时,是否需要进行协调控制有待进一步研究。保丽霞[8]在研究中指出交叉口关联度取值的范围为[0,1],当关联度小于0.5时,交叉口采用独立信号控制;当关联度大于等于0.5时,交叉口进行协调控制。现有研究多对交叉口车辆离散进行定量标定,以相邻交叉口间离散关联程度大小来判断交叉口间协调控制的优先级别,并指出相邻交叉口间离散关联度越大越适宜进行协调控制。
以路径关联度作为判断是否进行干线协调的依据是在研究交叉口离散关联性的基础上,增加对道路几何条件与信号协调控制之间关系的探讨。综合考虑交叉口的安全与效率因素,以第一类安全间距为标定点求解得最优路径关联度、以第二类安全间距为标定点求解得最优区间的最小值、以最大容许交叉口间距(暂取直行交通量占总交通量的比例为0.8进行计算)为标定点求解得最优区间的最大值,计算结果如表4所示。
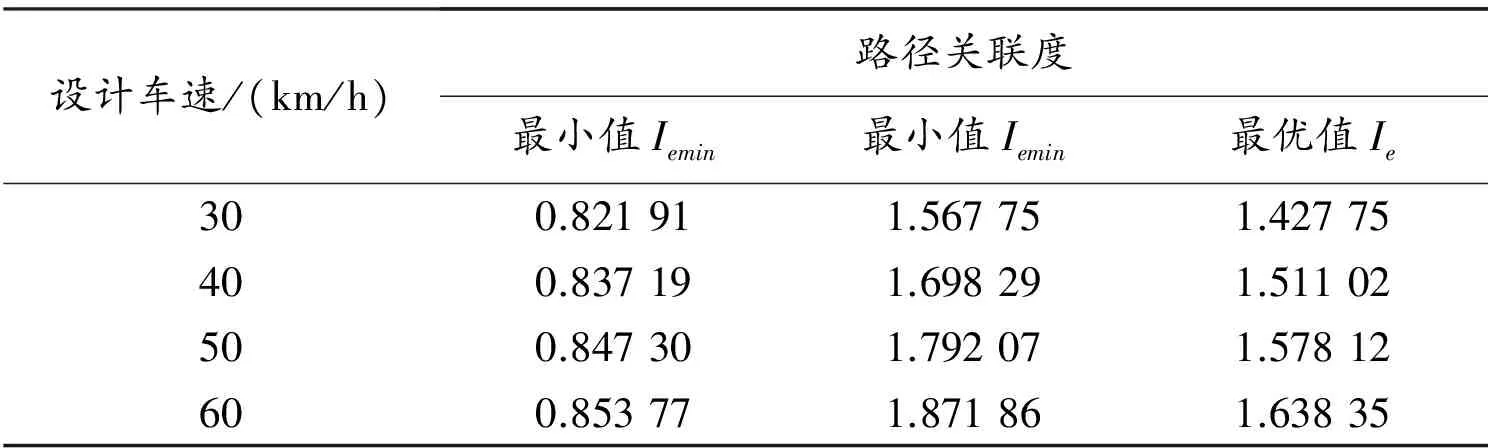
表4 最优交叉口路径关联度区间取值表
3.2 交叉口间距计算
在实际交叉口方案设计中,由于路网条件的限制,并不能随意改变交叉口几何条件使路径关联度达到最优,以期顺利施行干线协调控制。因此,可以通过确定路径关联度的最优区间范围,使得各交叉口关键路径关联度落在其区间范围内,为更好地实现干线协调控制提供合适的几何基础。为使干线协调效益达到较优水平,应尽可能确保关键路径的路径关联度接近最优交叉口路径关联度。若无法调整每一路径达到此标准,应确保各关键路径关联度介于最优区间范围内。在保证交叉口间距介于安全间距范围的基础上,尽量使路径关联度趋近于最优路径关联度取值。
对于交叉口间距确定,可以在干线道路总长度确定的情况下,结合考虑城市建筑用地,对交叉口间距进行微调整,使之适宜采用干线协调控制系统,提高道路服务水平。根据图6所示步骤通过计算机进行循环迭代计算,得出满足“所有关键路径关联度I∈[Iemin,Iemax],且最大容许交叉口间距≥各交叉口间距≥第一/二类交叉口安全间距”要求的交叉口间距取值。
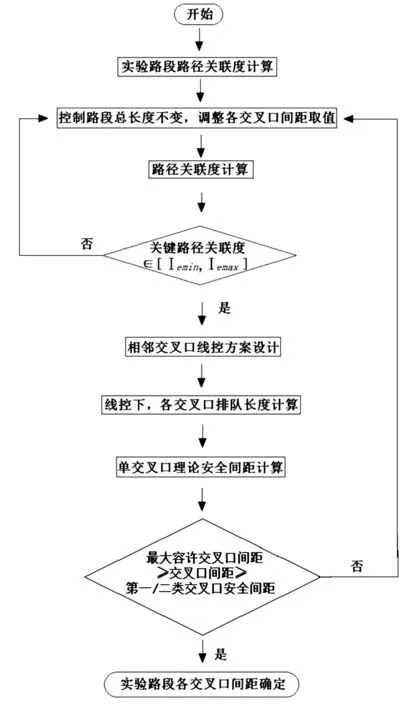
图6 交叉口间距求解流程图
4 结论
综合考虑交叉口交通安全与效率,并结合路径关联度模型,提出了适用于实施协调控制的干线交叉口间距确定方法。该模型不仅可用于新建或改建道路的交叉口间距确定,同时也适用
于实际交叉口的动态信号配时方案制定。有选择性地挑选关联性大的若干连续交叉口纳入同组信号配时方案,更易于协调控制效果的实现。
[1] 杨洁,过秀成,李岩,等.城市信号控制交叉口群路径关联度模型[J].交通运输系统工程与信息,2012,12(1):55-62.
[2] 美国运输部联邦公路局.交通控制系统手册(李海渊,译)[M].北京:人民交通出版社,1987.
[3]蒋金勇.单点及干道交通组织与信号配时改善研究[D].上海:同济大学,2007.
[4]中华人民共和国交通部.JTG D20—2006.公路路线设计规范[S].北京:中国标准出版社,2006.
[5] 李铁柱,李文权,周荣贵,等.高速公路加减速车道合流分流特征分析[J].公路交通科技,2009,18(4):89-91.
[6] 黄华华,蔡冬军.车头时距对道路通行能力的修正系数研究[J].城市交通,2011,10(6):1-4.
[7] EDMOND C C.How to Decide the Interconnection of Isolated Traffic Signals[C].Proceedings of the 1985 Winter Simulation Conference,1985.
[8] 保丽霞.基于车队离散模型的交叉口关联度量化方法研究与试验[J].公路交通科技,2011,28(1):1-8.
